Mecánica cuántica | explica cómo funciona el universo a una escala más pequeña que los átomos
La mecánica cuántica explica cómo funciona el universo a una escala menor que la de los átomos. También se denomina física cuántica o teoría cuántica. La mecánica es la parte de la física que explica cómo se mueven las cosas y quantum es la palabra latina que significa "cuánto". Un cuanto de energía es la menor cantidad posible (o la menor cantidad extra), y la mecánica cuántica describe cómo se mueve o interactúa esa energía.
Los átomos se consideraron durante mucho tiempo las piezas más pequeñas de la materia, pero la ciencia moderna ha demostrado que existen partículas subatómicas aún más pequeñas, como los protones, los neutrones y los electrones. La mecánica cuántica describe cómo funcionan las partículas que componen los átomos.
La mecánica cuántica también nos dice cómo funcionan las ondas electromagnéticas (como la luz). La dualidad onda-partícula significa que las partículas se comportan como ondas y las ondas se comportan como partículas. (No son dos tipos de cosas, son algo parecido a ambas: ésta es su dualidad). Gran parte de la física y la química modernas pueden describirse y comprenderse utilizando las reglas matemáticas de la mecánica cuántica.
Las matemáticas utilizadas para estudiar las partículas subatómicas y las ondas electromagnéticas son muy complejas porque actúan de forma muy extraña.
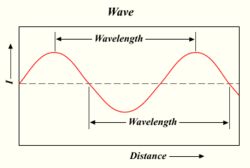
La longitud de onda de una onda de luz
Ondas y fotones
Los fotones son partículas del tamaño de un punto, más pequeñas que los átomos. Los fotones son como "paquetes" o envases de energía. Las fuentes de luz, como las velas o los láseres, producen luz en trozos llamados fotones.
Cuantos más fotones produzca una lámpara, más brillante será la luz. La luz es una forma de energía que se comporta como las ondas del agua o las ondas de radio. La distancia entre la parte superior de una onda y la parte superior de la siguiente se denomina "longitud de onda". Cada fotón lleva una determinada cantidad, o 'quantum', de energía en función de su longitud de onda.
El color de una luz depende de su longitud de onda. El color violeta (el color inferior o más interno del arco iris) tiene una longitud de onda de unos 400 nm ("nanómetros"), que son 0,00004 centímetros o 0,000016 pulgadas. Los fotones con longitudes de onda de 10-400 nm se denominan luz ultravioleta (o UV). Dicha luz no puede ser vista por el ojo humano. En el otro extremo del espectro, la luz roja tiene unos 700 nm. La luz infrarroja tiene entre 700 nm y 300.000 nm. Los ojos humanos tampoco son sensibles a la luz infrarroja.
Las longitudes de onda no siempre son tan pequeñas. Las ondas de radio tienen longitudes de onda más largas. Las longitudes de onda de una radio FM pueden tener varios metros de longitud (por ejemplo, las emisoras que transmiten en 99.5 FM están emitiendo energía radioeléctrica con una longitud de onda de unos 3 metros, que son unos 3 metros). Cada fotón tiene una determinada cantidad de energía relacionada con su longitud de onda. Cuanto más corta sea la longitud de onda de un fotón, mayor será su energía. Por ejemplo, un fotón ultravioleta tiene más energía que un fotón infrarrojo.
La longitud de onda y la frecuencia (el número de veces que la onda se eleva por segundo) son inversamente proporcionales, lo que significa que una longitud de onda más larga tendrá una frecuencia más baja, y viceversa. Si el color de la luz es infrarrojo (de menor frecuencia que la luz roja), cada fotón puede calentar lo que golpea. Así, si se apunta a una persona con una lámpara de infrarrojos fuerte (una lámpara de calor), esa persona sentirá calor, o incluso calor, debido a la energía almacenada en los numerosos fotones. La superficie de la lámpara de infrarrojos puede incluso calentarse lo suficiente como para quemar a alguien que la toque. Los humanos no podemos ver la luz infrarroja, pero podemos sentir la radiación en forma de calor. Por ejemplo, una persona que pase por delante de un edificio de ladrillos que ha sido calentado por el sol sentirá el calor del edificio sin tener que tocarlo.
Las ecuaciones matemáticas de la mecánica cuántica son abstractas, lo que significa que es imposible conocer con seguridad las propiedades físicas exactas de una partícula (como su posición o su momento). En su lugar, una función matemática llamada función de onda proporciona información sobre la probabilidad de que una partícula tenga una propiedad determinada. Por ejemplo, la función de onda puede decirle cuál es la probabilidad de que una partícula se encuentre en un lugar determinado, pero no puede decirle dónde está con seguridad. Debido a esta incertidumbre y a otros factores, no se puede utilizar la mecánica clásica (la física que describe cómo se mueven los objetos grandes) para predecir el movimiento de las partículas cuánticas.
La luz ultravioleta tiene una frecuencia más alta que la luz violeta, de manera que ni siquiera se encuentra en la gama de la luz visible. Cada fotón de la gama ultravioleta tiene mucha energía, la suficiente para dañar las células de la piel y provocar una quemadura solar. De hecho, la mayoría de las formas de quemaduras solares no son causadas por el calor; son causadas por la alta energía de los rayos UV del sol que dañan las células de la piel. Incluso las frecuencias más altas de luz (o radiación electromagnética) pueden penetrar más profundamente en el cuerpo y causar aún más daño. Los rayos X tienen tanta energía que pueden penetrar profundamente en el cuerpo humano y matar las células. Los seres humanos no pueden ver ni sentir la luz ultravioleta ni los rayos X. Sólo pueden saber que han estado bajo esa luz de alta frecuencia cuando sufren una quemadura por radiación. Los ámbitos en los que es importante matar los gérmenes suelen utilizar lámparas ultravioletas para destruir bacterias, hongos, etc. Los rayos X se utilizan a veces para matar las células cancerosas.
La mecánica cuántica comenzó cuando se descubrió que si una partícula tiene una determinada frecuencia, debe tener también una determinada cantidad de energía. La energía es proporcional a la frecuencia (E ∝ f). Cuanto más alta es la frecuencia, más energía tiene un fotón y más daño puede hacer. La mecánica cuántica creció posteriormente para explicar la estructura interna de los átomos. La mecánica cuántica también explica la forma en que un fotón puede interferir consigo mismo, y muchas otras cosas nunca imaginadas en la física clásica.

El negro de la izquierda es ultravioleta (alta frecuencia); el de la derecha es infrarrojo (baja frecuencia).
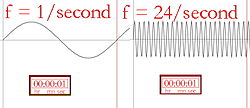
Descripción pictórica de la frecuencia
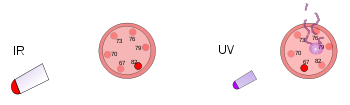
A la izquierda, un termómetro de plástico está bajo una lámpara de calor brillante. Esta radiación infrarroja calienta pero no daña el termómetro. A la derecha, otro termómetro de plástico recibe el impacto de una luz ultravioleta de baja intensidad. Esta radiación daña pero no calienta el termómetro.
Cuantización
Max Planck descubrió la relación entre la frecuencia y la energía. Nadie antes había adivinado que la frecuencia es directamente proporcional a la energía (esto significa que cuando una de ellas se duplica, la otra también lo hace). Bajo las llamadas unidades naturales, entonces el número que representa la frecuencia de un fotón representaría también su energía. La ecuación sería entonces
lo que significa que la energía es igual a la frecuencia.
Pero de la forma en que creció la física, no había una conexión natural entre las unidades que se utilizaban para medir la energía y las unidades comúnmente utilizadas para medir el tiempo (y por tanto la frecuencia). Así que la fórmula que Planck elaboró para que los números salieran bien fue
o, la energía es igual a h por la frecuencia. Esta h es un número llamado constante de Planck en honor a su descubridor.
La mecánica cuántica se basa en el conocimiento de que un fotón de una determinada frecuencia significa un fotón de una determinada cantidad de energía. Además de esa relación, un tipo específico de átomo sólo puede emitir ciertas frecuencias de radiación, por lo que también sólo puede emitir fotones que tengan ciertas cantidades de energía.
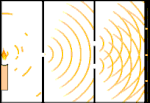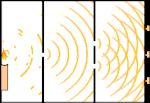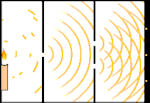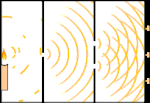
Experimento de la doble rendija: la luz va desde la fuente luminosa de la izquierda hasta las franjas (marcadas en el borde negro) de la derecha.
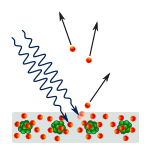
Efecto fotoeléctrico: los fotones chocan con el metal y los electrones son empujados.
Historia
Isaac Newton pensaba que la luz estaba hecha de cosas muy pequeñas que ahora llamaríamos partículas (se refería a ellas como "corpúsculos"). Christiaan Huygens pensaba que la luz estaba hecha de ondas. Los científicos pensaron que una cosa no puede ser una partícula y una onda al mismo tiempo.
Los científicos hicieron experimentos para averiguar si la luz estaba hecha de partículas o de ondas. Descubrieron que ambas ideas eran correctas: la luz era de alguna manera tanto ondas como partículas. El experimento de la doble rendija realizado por Thomas Young demostró que la luz debía actuar como una onda. El efecto fotoeléctrico descubierto por Albert Einstein demostró que la luz debía actuar como partículas que portaban cantidades específicas de energía, y que las energías estaban ligadas a sus frecuencias. Este resultado experimental se denomina "dualidad onda-partícula" en la mecánica cuántica. Más tarde, los físicos descubrieron que todo se comporta a la vez como una onda y como una partícula, no sólo la luz. Sin embargo, este efecto es mucho menor en los objetos grandes.
Estas son algunas de las personas que descubrieron las partes básicas de la mecánica cuántica: Max Planck, Albert Einstein, Satyendra Nath Bose, Niels Bohr, Louis de Broglie, Max Born, Paul Dirac, Werner Heisenberg, Wolfgang Pauli, Erwin Schrödinger, John von Neumann y Richard Feynman. Realizaron sus trabajos en la primera mitad del siglo XX.

De izquierda a derecha: Max Planck, Albert Einstein, Niels Bohr, Louis de Broglie, Max Born, Paul Dirac, Werner Heisenberg, Wolfgang Pauli, Erwin Schrödinger, Richard Feynman.
Más allá de Planck
Las fórmulas e ideas de la mecánica cuántica se hicieron para explicar la luz que sale del hidrógeno incandescente. La teoría cuántica del átomo también tenía que explicar por qué el electrón se mantiene en su órbita, algo que otras ideas no eran capaces de explicar. De las ideas más antiguas se desprendía que el electrón tendría que caer en el centro del átomo porque comienza siendo mantenido en su órbita por su propia energía, pero que perdería rápidamente su energía al girar en su órbita. (Esto se debe a que se sabía que los electrones y otras partículas cargadas emiten luz y pierden energía cuando cambian de velocidad o giran).
Las lámparas de hidrógeno funcionan como las de neón, pero éstas tienen su propio grupo de colores (y frecuencias) de luz. Los científicos aprendieron que podían identificar todos los elementos por los colores de luz que producen. Sólo que no pudieron averiguar cómo se determinaban las frecuencias.
Entonces, un matemático suizo llamado Johann Balmer descubrió una ecuación que indicaba cuál sería λ (lambda, por longitud de onda):
donde B es un número que Balmer determinó como igual a 364,56 nm.
Esta ecuación sólo funcionaba para la luz visible de una lámpara de hidrógeno. Pero más tarde, la ecuación se hizo más general:
donde R es la constante de Rydberg, igual a 0,0110 nm−1 , y n debe ser mayor que m.
Poniendo diferentes números para m y n, es fácil predecir las frecuencias para muchos tipos de luz (ultravioleta, visible e infrarroja). Para ver cómo funciona esto, vaya a Hiperfísica y baje más allá de la mitad de la página. (Utilice H = 1 para el hidrógeno).
En 1908, Walter Ritz elaboró el principio de combinación de Ritz que muestra cómo ciertos espacios entre frecuencias se repiten. Esto resultó ser importante para Werner Heisenberg varios años después.
En 1905, Albert Einstein utilizó la idea de Planck para demostrar que un haz de luz está formado por un flujo de partículas llamadas fotones. La energía de cada fotón depende de su frecuencia. La idea de Einstein es el comienzo de la idea de la mecánica cuántica de que todas las partículas subatómicas como los electrones, protones, neutrones y otras son ondas y partículas al mismo tiempo. (Véase la imagen del átomo con el electrón como ondas en el átomo.) Esto condujo a una teoría sobre las partículas subatómicas y las ondas electromagnéticas llamada dualidad onda-partícula. En ella, las partículas y las ondas no eran ni lo uno ni lo otro, sino que tenían ciertas propiedades de ambos.
En 1913, Niels Bohr propuso la idea de que los electrones sólo podían ocupar determinadas órbitas alrededor del núcleo de un átomo. Según la teoría de Bohr, los números llamados m y n en la ecuación anterior podían representar órbitas. La teoría de Bohr decía que los electrones podían empezar en alguna órbita m y terminar en alguna órbita n, o que un electrón podía empezar en alguna órbita n y terminar en alguna órbita m, por lo que si un fotón choca con un electrón, su energía será absorbida, y el electrón se moverá a una órbita superior debido a esa energía extra. Según la teoría de Bohr, si un electrón cae de una órbita superior a una inferior, tendrá que ceder energía en forma de fotón. La energía del fotón será igual a la diferencia de energía entre las dos órbitas, y la energía de un fotón hace que tenga una frecuencia y un color determinados. La teoría de Bohr proporcionó una buena explicación de muchos aspectos de los fenómenos subatómicos, pero no logró responder por qué cada uno de los colores de luz producidos por el hidrógeno incandescente (y por el neón incandescente o cualquier otro elemento) tiene un brillo propio, y las diferencias de brillo son siempre las mismas para cada elemento.
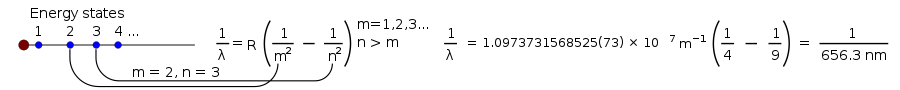
Cuando Niels Bohr presentó su teoría, ya se conocían casi todos los aspectos de la luz producida por una lámpara de hidrógeno, pero los científicos seguían sin poder explicar el brillo de cada una de las líneas producidas por el hidrógeno incandescente.
Werner Heisenberg se encargó de explicar el brillo o la "intensidad" de cada línea. No pudo utilizar ninguna regla sencilla como la que había ideado Balmer. Tuvo que utilizar las dificilísimas matemáticas de la física clásica que lo calcula todo en términos de cosas como la masa (peso) de un electrón, la carga (fuerza eléctrica estática) de un electrón y otras cantidades minúsculas. La física clásica ya tenía respuestas para el brillo de las bandas de color que produce una lámpara de hidrógeno, pero la teoría clásica decía que debía haber un arco iris continuo, y no cuatro bandas de color separadas. La explicación de Heisenberg es:
Existe una ley que dice qué frecuencias de luz producirá el hidrógeno brillante. Tiene que predecir las frecuencias espaciadas cuando los electrones implicados se mueven entre órbitas cercanas al núcleo (centro) del átomo, pero también tiene que predecir que las frecuencias se acercarán cada vez más a medida que observemos lo que hace el electrón al moverse entre órbitas cada vez más alejadas. También predecirá que las diferencias de intensidad entre las frecuencias se acercan cada vez más a medida que nos alejamos. Donde la física clásica ya da las respuestas correctas mediante un conjunto de ecuaciones, la nueva física tiene que dar las mismas respuestas pero mediante ecuaciones diferentes.
La física clásica utiliza los métodos matemáticos de Joseph Fourier para hacer una imagen matemática del mundo físico, Utiliza colecciones de curvas suaves que van juntas para hacer una curva suave que da, en este caso, las intensidades para la luz de todas las frecuencias de alguna luz. Pero no es correcto porque esa curva suave sólo aparece en las frecuencias más altas. En las frecuencias más bajas, siempre hay puntos aislados y nada conecta los puntos. Así que, para hacer un mapa del mundo real, Heisenberg tuvo que hacer un gran cambio. Tuvo que hacer algo para elegir sólo los números que coincidieran con lo que se veía en la naturaleza. A veces se dice que "adivinó" estas ecuaciones, pero no estaba haciendo conjeturas a ciegas. Encontró lo que necesitaba. Los números que calculó pondrían puntos en un gráfico, pero no habría ninguna línea dibujada entre los puntos. Y hacer una "gráfica" sólo de puntos para cada conjunto de cálculos habría desperdiciado mucho papel y no habría conseguido nada. Heisenberg encontró una forma de predecir eficazmente las intensidades para diferentes frecuencias y de organizar esa información de forma útil.
Sólo utilizando la regla empírica dada anteriormente, la que Balmer puso en marcha y Rydberg mejoró, podemos ver cómo obtener un conjunto de números que ayudarían a Heisenberg a obtener el tipo de imagen que quería:
La regla dice que cuando el electrón pasa de una órbita a otra gana o pierde energía, según se aleje o se acerque al centro. Así que podemos poner estas órbitas o niveles de energía en forma de encabezados a lo largo de la parte superior y lateral de una cuadrícula. Por razones históricas la órbita más baja se llama n, y la siguiente órbita hacia fuera se llama n - a, luego viene n - b, y así sucesivamente. Resulta confuso que utilizaran números negativos cuando los electrones en realidad estaban ganando energía, pero así es.
Dado que la regla de Rydberg nos da las frecuencias, podemos utilizar esa regla para poner números en función de dónde vaya el electrón. Si el electrón comienza en n y termina en n, entonces no ha ido realmente a ninguna parte, por lo que no ha ganado energía ni la ha perdido. Por tanto, la frecuencia es 0. Si el electrón comienza en n-a y termina en n, entonces ha caído de una órbita superior a una inferior. Si lo hace, entonces pierde energía, y la energía que pierde aparece como un fotón. El fotón tiene una determinada cantidad de energía, e, y eso está relacionado con una determinada frecuencia f por la ecuación e = h f. Así que sabemos que un determinado cambio de órbita va a producir una determinada frecuencia de la luz, f. Si el electrón comienza en n y termina en n - a, eso significa que ha pasado de una órbita inferior a una órbita superior. Eso sólo ocurre cuando un fotón de una determinada frecuencia y energía entra desde el exterior, es absorbido por el electrón y le da su energía, y eso es lo que hace que el electrón salga a una órbita superior. Así que, para que todo tenga sentido, escribimos esa frecuencia como un número negativo. Había un fotón con una frecuencia determinada y ahora se la han quitado.
Así que podemos hacer una retícula como ésta, donde f(a←b) significa la frecuencia implicada cuando un electrón pasa del estado energético (órbita) b al estado energético a (De nuevo, las secuencias parecen al revés, pero es la forma en que se escribían originalmente):
Rejilla de f
| Estados de los electrones | n | n-a | n-b | n-c | .... | |
| n | f(n←n) | f(n←n-a) | f(n←n-b) | f(n←n-c) | ..... | |
| n-a | f(n-a←n) | f(n-a←n-a) | f(n-a←n-b) | f(n-a←n-c) | ..... | |
| n-b | f(n-b←n) | f(n-b←n-a) | f(n-b←n-b) | f(n-b←n-c) | ..... | |
| transición.... | ..... | ..... | ..... | ..... |
Heisenberg no hizo las cuadrículas así. Sólo hizo los cálculos que le permitieran obtener las intensidades que buscaba. Pero para ello tuvo que multiplicar dos amplitudes (lo que mide una onda) para calcular la intensidad. (En la física clásica, la intensidad es igual a la amplitud al cuadrado.) Hizo una ecuación de aspecto extraño para resolver este problema, escribió el resto de su trabajo, se lo entregó a su jefe y se fue de vacaciones. El Dr. Born miró su curiosa ecuación y le pareció un poco loca. Debió de preguntarse: "¿Por qué me ha dado Heisenberg esta cosa tan extraña? ¿Por qué tiene que hacerlo así?". Entonces se dio cuenta de que estaba viendo un plano de algo que ya conocía muy bien. Estaba acostumbrado a llamar matriz a la cuadrícula o tabla que podíamos escribir haciendo, por ejemplo, todas las matemáticas de las frecuencias. Y la extraña ecuación de Heisenberg era una regla para multiplicar dos de ellas. Max Born era un matemático muy, muy bueno. Sabía que como las dos matrices (rejillas) que se multiplicaban representaban cosas diferentes (como la posición (x,y,z) y el momento (mv), por ejemplo), cuando se multiplica la primera matriz por la segunda se obtiene una respuesta y cuando se multiplica la segunda matriz por la primera se obtiene otra respuesta. Aunque no sabía de matemáticas matriciales, Heisenberg ya vio este problema de las "diferentes respuestas" y le molestó. Pero el Dr. Born era tan buen matemático que vio que la diferencia entre la primera multiplicación matricial y la segunda multiplicación matricial siempre iba a implicar la constante de Planck, h, multiplicada por la raíz cuadrada de uno negativo, i. Así que a los pocos días del descubrimiento de Heisenberg ya tenían las matemáticas básicas de lo que a Heisenberg le gustaba llamar el "principio de indeterminación". Por "indeterminación" Heisenberg quería decir que algo como un electrón no se puede fijar hasta que se fija. Es un poco como una medusa que siempre se está aplastando y no puede estar "en un sitio" a menos que se la mate. Más tarde, la gente se acostumbró a llamarlo "principio de incertidumbre de Heisenberg", lo que hizo que mucha gente cometiera el error de pensar que los electrones y cosas así están realmente "en algún sitio", pero que sólo estamos inseguros en nuestras propias mentes. Esa idea es errónea. No es de lo que hablaba Heisenberg. Tener problemas para medir algo es un problema, pero no es el problema del que hablaba Heisenberg.
La idea de Heisenberg es muy difícil de entender, pero podemos aclararla con un ejemplo. En primer lugar, empezaremos a llamar a estas cuadrículas "matrices", porque pronto tendremos que hablar de la multiplicación de matrices.
Supongamos que partimos de dos tipos de medidas, la posición (q) y el momento (p). En 1925, Heisenberg escribió una ecuación como esta

No lo sabía, pero esta ecuación da un plano para escribir dos matrices (cuadrículas) y para multiplicarlas. Las reglas para multiplicar una matriz por otra son un poco confusas, pero aquí están las dos matrices según el plano, y luego su producto:
Matriz de p
| Estados de los electrones | n-a | n-b | n-c | .... | |
| n | p(n←n-a) | p(n←n-b) | p(n←n-c) | ..... | |
| n-a | p(n-a←n-a) | p(n-a←n-b) | p(n-a←n-c) | ..... | |
| n-b | p(n-b←n-a) | p(n-b←n-b) | p(n-b←n-c) | ..... | |
| transición.... | ..... | ..... | ..... | ..... |
Matriz de q
| Estados de los electrones | n-b | n-c | n-d | .... | |
| n-a | q(n-a←n-b) | q(n-a←n-c) | q(n-a←n-d) | ..... | |
| n-b | q(n-b←n-b) | q(n-b←n-c) | q(n-b←n-d) | ..... | |
| n-c | q(n-c←n-b) | q(n-c←n-c) | q(n-c←n-d) | ..... | |
| transición.... | ..... | ..... | ..... | ..... |
La matriz para el producto de las dos matrices anteriores, tal como se especifica en la ecuación correspondiente del artículo de Heisenberg de 1925, es:
| Estados de los electrones | n-b | n-c | n-d | ..... |
| n | A | ..... | ..... | ..... |
| n-a | ..... | B | ..... | ..... |
| n-b | ..... | ..... | C | ..... |
Dónde:
A=p(n←n-a)*q(n-a←n-b)+p(n←n-b)*q(n-b←n-b)+p(n←n-c)*q(n-c←n-b)+.....
B=p(n-a←n-a)*q(n-a←n-c)+p(n-a←n-b)*q(n-b←n-c)+p(n-a←n-c)*q(n-c←n-c)+.....
C=p(n-b←n-a)*q(n-a←n-d)+p(n-b←n-b)*q(n-b←n-d)+p(n-b←n-c)*q(n-d←n-d)+.....
y así sucesivamente.
Si se invirtieran las matrices, resultarían los siguientes valores:
A=q(n←n-a)*p(n-a←n-b)+q(n←n-b)*p(n-b←n-b)+q(n←n-c)*p(n-c←n-b)+.....
B=q(n-a←n-a)*p(n-a←n-c)+q(n-a←n-b)*p(n-b←n-c)+q(n-a←n-c)*p(n-c←n-c)+.....
C=q(n-b←n-a)*p(n-a←n-d)+q(n-b←n-b)*p(n-b←n-d)+q(n-b←n-c)*p(n-d←n-d)+.....
y así sucesivamente.
Observe cómo al cambiar el orden de la multiplicación cambian los números, paso a paso, que realmente se multiplican.

Luz visible emitida por el hidrógeno incandescente. (Longitudes de onda en nanómetros.)
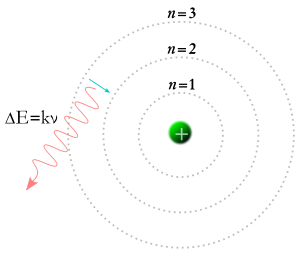
Un electrón cae a la órbita inferior y se crea un fotón.
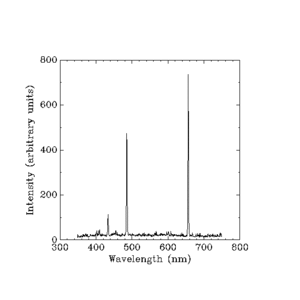
Intensidades espaciadas en unidades arbitrarias
Más allá de Heisenberg
El trabajo de Werner Heisenberg pareció romper un atasco. Muy pronto, surgieron otras muchas formas de explicar las cosas de la mano de gente como Louis de Broglie, Max Born, Paul Dirac, Wolfgang Pauli y Erwin Schrödinger. El trabajo de cada uno de estos físicos es su propia historia. Las matemáticas utilizadas por Heisenberg y los anteriores no son muy difíciles de entender, pero las ecuaciones se complicaron rápidamente a medida que los físicos profundizaban en el mundo atómico.
Otros misterios
En los primeros días de la mecánica cuántica, Albert Einstein sugirió que si era correcta, la mecánica cuántica significaría que habría "acción fantasmal a distancia". Resultó que la mecánica cuántica era correcta, y que lo que Einstein había utilizado como razón para rechazar la mecánica cuántica ocurría realmente. Este tipo de "conexión espeluznante" entre ciertos sucesos cuánticos se llama ahora "entrelazamiento cuántico".
Cuando un experimento reúne dos cosas (fotones, electrones, etc.), entonces deben compartir una descripción común en la mecánica cuántica. Cuando se separan posteriormente, mantienen la misma descripción mecánica cuántica o "estado". En el diagrama, una característica (por ejemplo, el espín "arriba") se dibuja en rojo, y su compañera (por ejemplo, el espín "abajo") se dibuja en azul. La banda púrpura significa que cuando, por ejemplo, dos electrones se juntan, la pareja comparte ambas características. Así, ambos electrones pueden mostrar un espín hacia arriba o un espín hacia abajo. Cuando más tarde se separan, uno se queda en la Tierra y otro va a algún planeta de la estrella Alfa Centauri, siguen teniendo cada uno ambos espines. En otras palabras, cada uno de ellos puede "decidir" mostrarse como un electrón de espín ascendente o como un electrón de espín descendente. Pero si más tarde alguien mide al otro, éste debe "decidir" mostrarse con el espín opuesto.
Einstein argumentó que a una distancia tan grande era una locura pensar que forzar a un electrón a mostrar su espín haría que el otro electrón mostrara de alguna manera una característica opuesta. Dijo que los dos electrones debían haber sido de espín hacia arriba o hacia abajo todo el tiempo, pero que la mecánica cuántica no podía predecir qué característica tenía cada electrón. El hecho de no poder predecir, de sólo poder observar uno de ellos con el experimento adecuado, significaba que la mecánica cuántica no podía dar cuenta de algo importante. Por tanto, dijo Einstein, la mecánica cuántica tenía un gran agujero. La mecánica cuántica estaba incompleta.
Más tarde, resultó que los experimentos demostraron que era Einstein quien estaba equivocado.
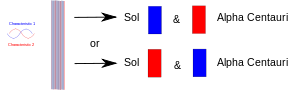
Se separan dos partículas enredadas: una en la Tierra y otra llevada a algún planeta lejano. La medición de una de ellas la obliga a "decidir" qué papel tomar, y la otra debe entonces tomar el otro papel cada vez que (después de eso) se le mida.
Principio de incertidumbre de Heisenberg
En 1925, Werner Heisenberg describió el principio de incertidumbre, que dice que cuanto más sepamos sobre el lugar en el que se encuentra una partícula, menos podremos saber sobre la velocidad a la que va y en qué dirección. En otras palabras, cuanto más sepamos sobre la velocidad y la dirección de algo pequeño, menos podremos saber sobre su posición. Los físicos suelen hablar del impulso en estas discusiones en lugar de hablar de la velocidad. El impulso no es más que la velocidad de algo en una dirección determinada multiplicada por su masa.
La razón que subyace al principio de incertidumbre de Heisenberg dice que nunca podemos conocer tanto la ubicación como el momento de una partícula. Como la luz es una partícula abundante, se utiliza para medir otras partículas. La única forma de medirla es hacer rebotar la onda luminosa en la partícula y registrar los resultados. Si se utiliza un haz de luz de alta energía, o de alta frecuencia, podemos saber con precisión dónde se encuentra, pero no podemos saber a qué velocidad iba. Esto se debe a que el fotón de alta energía transfiere energía a la partícula y cambia la velocidad de ésta. Si utilizamos un fotón de baja energía, podemos saber a qué velocidad va, pero no dónde está. Esto se debe a que estamos utilizando luz con una longitud de onda más larga. La mayor longitud de onda significa que la partícula podría estar en cualquier lugar a lo largo del tramo de la onda.
El principio también dice que hay muchos pares de mediciones para los que no podemos conocer ambos sobre ninguna partícula (algo muy pequeño), por mucho que lo intentemos. Cuanto más aprendamos sobre uno de tales pares, menos podremos saber sobre el otro.
Incluso Albert Einstein tuvo problemas para aceptar un concepto tan extraño, y en un conocido debate dijo: "Dios no juega a los dados". A esto, el físico danés Niels Bohr respondió famosamente: "Einstein, no le digas a Dios lo que tiene que hacer".
Usos de la mecánica cuántica
Los electrones rodean el núcleo de cada átomo. Los enlaces químicos unen los átomos para formar moléculas. Un enlace químico une dos átomos cuando los electrones se comparten entre esos átomos. Así pues, la mecánica cuántica es la física del enlace químico y de la química. La mecánica cuántica nos ayuda a entender cómo se forman las moléculas y cuáles son sus propiedades.
La mecánica cuántica también puede ayudarnos a entender las cosas grandes, como las estrellas e incluso todo el universo. La mecánica cuántica es una parte muy importante de la teoría de cómo empezó el universo llamada Big Bang.
Todo lo que está hecho de materia es atraído por otra materia debido a una fuerza fundamental llamada gravedad. La teoría de Einstein que explica la gravedad se llama teoría de la relatividad general. Un problema de la física moderna es que algunas conclusiones de la mecánica cuántica no parecen coincidir con la teoría de la relatividad general.
La mecánica cuántica es la parte de la física que puede explicar por qué toda la tecnología electrónica funciona como lo hace. Así, la mecánica cuántica explica cómo funcionan los ordenadores, porque los ordenadores son máquinas electrónicas. Pero los diseñadores de los primeros equipos informáticos de alrededor de 1950 o 1960 no necesitaban pensar en la mecánica cuántica. Los diseñadores de radios y televisores de aquella época tampoco pensaron en la mecánica cuántica. Sin embargo, el diseño de los circuitos integrados más potentes y de las tecnologías de memoria de los ordenadores de los últimos años sí requiere de la mecánica cuántica.
La mecánica cuántica también ha hecho posibles tecnologías como:
Por qué la mecánica cuántica es difícil de aprender
La mecánica cuántica es un tema desafiante por varias razones:
- La mecánica cuántica explica las cosas de forma muy diferente a lo que aprendemos sobre el mundo cuando somos niños.
- La comprensión de la mecánica cuántica requiere más matemáticas que el álgebra y el cálculo simple. También requiere álgebra matricial, números complejos, teoría de la probabilidad y ecuaciones diferenciales parciales.
- Los físicos no están seguros de lo que algunas de las ecuaciones de la mecánica cuántica nos dicen sobre el mundo real.
- La mecánica cuántica sugiere que los átomos y las partículas subatómicas se comportan de formas extrañas, completamente diferentes a todo lo que vemos en nuestra vida cotidiana.
- La mecánica cuántica describe cosas que son extremadamente pequeñas, por lo que no podemos ver algunas de ellas sin un equipo especial, y no podemos ver muchas de ellas en absoluto.
La mecánica cuántica describe la naturaleza de una manera diferente a como solemos pensar en la ciencia. Nos dice la probabilidad de que ocurran algunas cosas, en lugar de decirnos que ciertamente ocurrirán.
Un ejemplo es el experimento de la doble rendija de Young. Si disparamos fotones individuales (unidades individuales de luz) desde un láser a una hoja de película fotográfica, veremos un único punto de luz en la película revelada. Si ponemos una lámina de metal en medio, y hacemos dos rendijas muy estrechas en la lámina, cuando disparemos muchos fotones a la lámina de metal, y tengan que pasar por las rendijas, entonces veremos algo notable. A lo largo de toda la lámina revelada veremos una serie de bandas brillantes y oscuras. Podemos utilizar las matemáticas para saber exactamente dónde estarán las bandas brillantes y cómo de brillante fue la luz que las hizo, es decir, podemos saber de antemano cuántos fotones caerán en cada banda. Pero si ralentizamos el proceso y vemos dónde cae cada fotón en la pantalla, nunca podremos saber de antemano dónde aparecerá el siguiente. Podemos saber con seguridad que lo más probable es que un fotón caiga en la banda brillante del centro, y que cada vez es menos probable que un fotón aparezca en las bandas cada vez más alejadas del centro. Por lo tanto, sabemos con seguridad que las bandas serán más brillantes en el centro y se harán cada vez más tenues en los lugares más alejados. Pero nunca sabemos con seguridad qué fotón entrará en cada banda.
Una de las extrañas conclusiones de la teoría de la mecánica cuántica es el efecto del "gato de Schrödinger". No se puede hablar de ciertas propiedades de una partícula, como su posición, velocidad de movimiento, dirección de movimiento y "giro", hasta que algo las mida (un fotón que rebote en un electrón contaría como una medición de su posición, por ejemplo). Antes de la medición, la partícula se encuentra en una "superposición de estados", en la que sus propiedades tienen muchos valores al mismo tiempo. Schrödinger dijo que la mecánica cuántica parecía decir que si algo (como la vida o la muerte de un gato) estaba determinado por un suceso cuántico, entonces su estado estaría determinado por el estado resultante del suceso cuántico, pero sólo en el momento en que alguien mirara el estado del suceso cuántico. En el tiempo anterior a que se mire el estado del suceso cuántico, tal vez "el gato vivo y el muerto (perdón por la expresión) [estén] mezclados o embadurnados a partes iguales".
Constante de Planck reducida
La gente suele utilizar el símbolo ℏ 

Ejemplo
La partícula en un pozo unidimensional es el ejemplo más sencillo que demuestra que la energía de una partícula sólo puede tener valores específicos. Se dice que la energía está "cuantizada". El pozo tiene energía potencial cero dentro de un rango y tiene energía potencial infinita en todas partes fuera de ese rango. Para el caso unidimensional en la dirección 
Utilizando ecuaciones diferenciales, podemos averiguar que ψ 
o como

Las paredes de la caja significan que la función de onda debe tener una forma especial. La función de onda de la partícula debe ser cero siempre que las paredes sean infinitas. En cada pared:
Considere x = 0
- sen 0 = 0, cos 0 = 1.
Para satisfacer ψ = 0 que eliminar el término cos. Por tanto, D = 0
Ahora considere:
- en
, ψ
- Si
entonces ψ
para todo x. Esta solución no es útil.
- por lo tanto
debe ser cierto, dándonos
Podemos ver que 
Páginas relacionadas
- Onda electromagnética
- Electrón
- Fotón
- Enredo cuántico
- Ordenador cuántico
- Estado cuántico
- Ecuación de Schrödinger
Más información
- Cox, Brian; & Forshaw, Jeff (2011). El universo cuántico: Todo lo que puede ocurrir, ocurre. Allen Lane. ISBN 978-1-84614-432-5
Preguntas y respuestas
P: ¿Qué es la mecánica cuántica?
R: La mecánica cuántica es una rama de la física que explica cómo funciona el universo a una escala más pequeña que los átomos. También se conoce como física cuántica o teoría cuántica.
P: ¿Qué significa el término "cuántico"?
R: El término "quantum" procede del latín y significa "cuanto". Un cuanto de energía es la menor cantidad posible (o la menor cantidad extra), y la mecánica cuántica describe cómo se mueve o interactúa esa energía.
P: ¿Qué son las partículas subatómicas?
R: Las partículas subatómicas son partículas que componen los átomos, como los protones, los neutrones y los electrones. Son incluso más pequeñas que los átomos.
P: ¿Cómo describe la mecánica cuántica el funcionamiento de estas partículas?
R: La mecánica cuántica proporciona reglas matemáticas para estudiar las partículas subatómicas y las ondas electromagnéticas con el fin de comprender su comportamiento y sus interacciones entre sí.
P: ¿Qué es la dualidad onda-partícula?
R: La dualidad onda-partícula se refiere al hecho de que tanto las partículas como las ondas pueden comportarse como una sola - no son dos entidades distintas, sino algo así como ambas combinadas en un solo fenómeno.
P: ¿Cómo se puede describir la física moderna mediante la mecánica cuántica?
R: La física y la química modernas pueden explicarse aplicándoles las reglas matemáticas de la mecánica cuántica.
Buscar dentro de la enciclopedia









