Fórmula de Euler: identidad e^{ix}=cos x+i sin x en análisis complejo

Descubre la fórmula de Euler e^{ix}=cos x+i sin x: historia, demostración y aplicaciones en análisis complejo; conecta exponenciales y trigonometría para entender identidades clave.

En el análisis complejo, la fórmula de Euler, también llamada a veces relación de Euler, es una ecuación en la que intervienen números complejos y funciones trigonométricas. Más concretamente, afirma que

e i x = cos x + i sin x {\displaystyle e^{ix}=cos x+i\sin x}

donde x es un número real, e es el número de Euler e i es la unidad imaginaria.

Hace una relación entre las funciones trigonométricas y las funciones exponenciales de los números complejos. Lleva el nombre de Leonhard Euler, que la publicó en 1748. Cuando la publicó, Euler dijo que el ángulo debía ser un número real. Más tarde, resultó que la fórmula también funciona si el ángulo no es un número real, sino uno complejo.

Cuando el ángulo es π {\displaystyle \pi } y 2 π {\displaystyle 2\pi } , la fórmula de Euler se convierte en e i π = - 1 {\displaystyle e^{i\pi }=-1} y e i 2 π = 1 {\displaystyle e^{i2\pi }=1} , respectivamente.

Interpretación geométrica

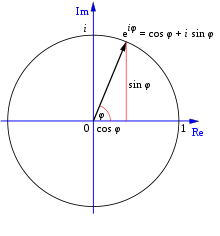
La fórmula de Euler establece una correspondencia natural entre la exponencial compleja y la rotación en el plano complejo. Si identificamos un número complejo z = x + iy con el punto (x,y) del plano, entonces multiplicar por e^{iθ} representa una rotación del plano alrededor del origen por un ángulo θ (medido en radianes). Por eso la exponencial compleja permite escribir en forma polar cualquier número complejo: un número distinto de cero se puede expresar como

re^{iθ} = r(\cos θ + i \sin θ), donde r = |z| es el módulo y θ = arg(z) es el argumento (ángulo).

Demostraciones (esbozos)

• Series de Taylor (más común en análisis): las series de Taylor alrededor de 0 son

  e^{ix} = Σ_{n=0}^{∞} (ix)^n/n!,

  cos x = Σ_{n=0}^{∞} (-1)^n x^{2n}/(2n)!,

  sin x = Σ_{n=0}^{∞} (-1)^n x^{2n+1}/(2n+1)!.

  Separando los términos pares e impares de la serie de e^{ix} y agrupando las potencias de i se obtienen exactamente las series de cos x y sin x, lo que da e^{ix} = cos x + i sin x.
• Ecuación diferencial: la función f(x)=e^{ix} satisface f'(x)=i f(x) y f(0)=1. La combinación g(x)=cos x + i sin x satisface la misma ecuación y condición inicial (pues g'(x)=-sin x + i cos x = i g(x), g(0)=1). Por unicidad de la solución del problema de valor inicial, f=g.
• Integrales y ángulos: también puede demostrarse usando definiciones de cos y sin por integrales o por la representación como proyecciones de la solución de la ecuación diferencial del oscilador armónico.

Fórmulas útiles y consecuencias

• Identidad de Euler: tomando x = π se obtiene e^{iπ} + 1 = 0, que relaciona las constantes fundamentales e, π, i, 1 y 0 en una sola expresión.
• Relaciones inversas:

  cos x = (e^{ix} + e^{-ix})/2,

  sin x = (e^{ix} - e^{-ix})/(2i).

• Multiplicatividad: e^{i(x+y)} = e^{ix} e^{iy}, lo que refleja que sumar ángulos corresponde a componer rotaciones.
• Fórmula de De Moivre: para entero n, (cos x + i sin x)^n = cos(nx) + i sin(nx), que se obtiene fácilmente elevando e^{ix} a la n.
• Raíces de la unidad: las n-ésimas raíces de 1 son e^{i2πk/n} para k = 0,1,...,n−1; se sitúan uniformemente en la circunferencia unidad del plano complejo.

Generalización a argumentos complejos

La fórmula se extiende a cualquier argumento complejo z = x + iy mediante la definición usual de la exponencial compleja:

e^{z} = e^{x+iy} = e^{x}e^{iy} = e^{x}(\cos y + i\sin y).

Así, para un argumento complejo aparece simultáneamente un factor de escala e^{x} (módulo) y una rotación e^{iy} (argumento).

Aplicaciones

• Análisis de Fourier: la representación de señales periódicas y transformadas utiliza exponentes complejos e^{iωt} por su sencillez algebraica y su relación directa con senos y cosenos.
• Electrotecnia: en circuitos de corriente alterna se usan fasores y exponentes complejos para representar amplitud y fase de tensiones y corrientes.
• Mecánica cuántica y física teórica: las ondas y amplitudes complejas se expresan con exponentes imaginarios, facilitando el cálculo de interferencias y propagación de fases.
• Teoría de números y polinomios: las raíces de la unidad, polinomios ciclotómicos y transformadas discretas (DFT/FFT) dependen de e^{i2πk/n}.

Observaciones finales

La fórmula de Euler es una herramienta central en matemáticas y física porque convierte problemas trigonométricos en problemas exponenciales (y viceversa), simplificando cálculos y proporcionando una visión geométrica clara (rotaciones y escalados). Además, su extensión al plano complejo y la conexión con series y ecuaciones diferenciales hacen de ella una piedra angular del análisis complejo y de muchas áreas aplicadas.

Preguntas y respuestas

P: ¿Qué es la fórmula de Euler?

P: ¿Quién publicó la fórmula de Euler?

P: ¿Funciona la fórmula cuando el ángulo no es un número real?

P: ¿Qué ocurre cuando el ángulo es pi?

P: ¿Qué ocurre cuando el ángulo es 2pi?

P: ¿Qué representa "e" en esta ecuación?

P: ¿Qué representa "i" en esta ecuación?

Búsqueda por letra