Función trigonométrica
En matemáticas, las funciones trigonométricas son un conjunto de funciones que relacionan los ángulos con los lados de un triángulo rectángulo. Hay muchas funciones trigonométricas, las 3 más comunes son el seno, el coseno y la tangente, seguidas de la cotangente, la secante y la cosecante. Las tres últimas se llaman funciones trigonométricas recíprocas porque actúan como recíprocas de otras funciones. La secante y la cosecante se utilizan raramente.
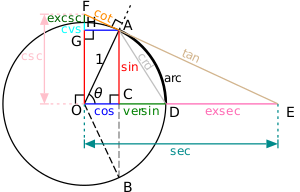
Todas las funciones trigonométricas de cualquier ángulo se pueden construir utilizando un círculo centrado en O con radio 1.

Funciones trigonométricas: Seno , Coseno , Tangente , Cosecante , Secante , Cotangente
Definición
Las funciones trigonométricas a veces se llaman también funciones circulares. Son funciones de un ángulo; son importantes para el estudio de los triángulos, entre otras muchas aplicaciones. Las funciones trigonométricas se definen comúnmente como cocientes de dos lados de un triángulo rectángulo que contiene el ángulo, y pueden definirse equivalentemente como las longitudes de varios segmentos de línea de un círculo unitario (un círculo que tiene un radio de uno).
Definiciones de triángulo rectángulo
Para definir las funciones trigonométricas del ángulo A, se parte de un triángulo rectángulo que contiene el ángulo A:
Utilizamos los siguientes nombres para los lados del triángulo:
- La hipotenusa es el lado opuesto al ángulo recto, o se define como el lado más largo de un triángulo rectángulo, en este caso h.
- El lado opuesto es el lado opuesto al ángulo que nos interesa, en este caso a.
- El lado adyacente es el que está en contacto con el ángulo que nos interesa y el ángulo recto, de ahí su nombre. En este caso el lado adyacente es b.
Se considera que todos los triángulos existen en la geometría euclidiana de forma que los ángulos interiores de cada triángulo suman π radianes (o 180°); por tanto, para un triángulo rectángulo los dos ángulos no rectos están entre cero y π/2 radianes. El lector debe tener en cuenta que las siguientes definiciones, en sentido estricto, sólo definen las funciones trigonométricas para los ángulos en este rango. Las extendemos a todo el conjunto de argumentos reales utilizando el círculo unitario, o exigiendo ciertas simetrías y que sean funciones periódicas.
1) El seno de un ángulo es la relación entre la longitud del lado opuesto y la longitud de la hipotenusa. En nuestro caso
sin A = hipotenusa opuesta = a h . {\displaystyle \sin A={frac {\textrm {opuesta}}{\textrm {hipotenusa}}={frac {a}{h}}. }
Obsérvese que este cociente no depende del triángulo rectángulo concreto elegido, siempre que contenga el ángulo A, ya que todos esos triángulos son semejantes.
El conjunto de ceros del seno (es decir, los valores de x {\displaystyle x} 

{ n π | n ∈ Z } . {\displaystyle \\\\\\Nde la izquierda} {\Nde la izquierda} {\Nde la izquierda} {\Nde la derecha} {\i1}Derecha{\i} {\i} }
2) El coseno de un ángulo es el cociente entre la longitud del lado adyacente y la longitud de la hipotenusa. En nuestro caso
cos A = hipotenusa adyacente = b h . {\displaystyle \cos A={frac {\textrm {adyacente}{textrm {hipotenusa}}={frac {b}{h}}. }
El conjunto de ceros del coseno es
{ π 2 + n π | n ∈ Z } . {\displaystyle \\\\\} izquierda + n\\pi {\bigg |}n\\\\} en \mathbb {Z} \...derecha...} }
3) La tangente de un ángulo es la relación entre la longitud del lado opuesto y la longitud del lado adyacente. En nuestro caso
tan A = opuesto adyacente = a b . {\displaystyle \tan A={frac {\textrm {opuesto}}{textrm {adyacente}}={frac {a}{b}}. }
El conjunto de ceros de la tangente es
{ n π | n ∈ Z } . {\displaystyle \\\\\\Nde la izquierda} {\Nde la izquierda} {\Nde la izquierda} {\Nde la derecha} {\i1}Derecha{\i} {\i} }
El mismo conjunto de la función seno desde
tan A = sin A cos A . {\displaystyle \tan A={frac {\sin A}{\cos A}}. }
Las tres funciones restantes se definen mejor utilizando las tres funciones anteriores.
4) La cosecante csc(A) es la inversa multiplicativa de sin(A), es decir, la relación entre la longitud de la hipotenusa y la longitud del lado opuesto:
csc A = hipotenusa opuesta = h a {\displaystyle \csc A={frac {\textrm {hipotenusa}}{\textrm {opuesta}}={\frac {h}{a}}
5) La secante sec(A) es la inversamultiplicativa de cos(A), es decir, la relación entre la longitud de la hipotenusa y la longitud del lado adyacente:
sec A = hipotenusa adyacente = h b {\displaystyle \sec A={frac {\textrm {hipotenusa}}{\textrm {adyacente}}={\frac {h}{b}}
6) La cotangente cot(A) es la inversa multiplicativa de tan(A), es decir, la relación entre la longitud del lado adyacente y la longitud del lado opuesto:
cot A = adyacente opuesto = b a {\displaystyle \cot A={\frac {\textrm {adyacente}}{\textrm {opuesto}}={\frac {b}{a}}
Definiciones por series de potencia
También se pueden definir las funciones trigonométricas mediante series de potencias:
¡sin x = x - x 3 3 ! ¡+ x 5 5 ! - ¡- x 7 7 ! ¡+ ⋯ = ∑ n = 0 ∞ ( - 1 ) n x 2 n + 1 ( 2 n + 1 ) ! {\displaystyle \sin x=x-{\frac {x^{3}{3!}}+{\frac {x^{5}{5!}}-{\frac {x^{7}{7!}}+cdots =\sum _{n=0}^{\infty}{{(-1)^{n}x^{2n+1}{(2n+1)!}}
¡cos x = 1 - x 2 2 ! ¡+ x 4 4 ! - ¡- x 6 6 ! ¡+ ⋯ = ∑ n = 0 ∞ ( - 1 ) n x 2 n ( 2 n ) ! {\displaystyle \cos x=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-{{\frac {x^{6}}{6!}}+cdots ={{suma _{n=0}^{\infty}{{(-1)^{n}x^{2n}}{(2n)!}}
y definir la tangente, la cotangente, la secante y la cosecante utilizando las identidades, ver más abajo.
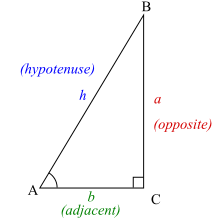
Un triángulo rectángulo siempre incluye un ángulo de 90° (π/2 radianes), aquí etiquetado como C. Los ángulos A y B pueden variar. Las funciones trigonométricas especifican las relaciones entre las longitudes de los lados y los ángulos interiores de un triángulo rectángulo.
Identidades
Algunas identidades importantes:
tan x = sin x cos x {\displaystyle \tan x={frac {\sin x}{\cos x}}
cot x = cos x sin x {\displaystyle \cot x={frac {\cos x}{\sin x}}
sec x = 1 cos x {\displaystyle \sec x={frac {1}{cos x}}
csc x = 1 sin x {\displaystyle \csc x={frac {1}{sin x}}
sen 2 x + cos 2 x = 1 {\displaystyle \sin ^{2}x+\cos ^{2}x=1}
sin 2 x = 2 sin x cos x {\displaystyle \sin 2x=2\sin x\cos x}
cos 2 x = cos x cos x - sin x sin x = cos 2 x - sin 2 x = 2 cos 2 x - 1 = 1 - 2 sin 2 x {\displaystyle \cos 2x=cos x\cos x-\sin x\sin x=\cos ^{2}x-\sin ^{2}x=2cos ^{2}x-1=1-2\sin ^{2}x}
tan 2 x = 2 tan x 1 - tan 2 x {\displaystyle \tan 2x={frac {2\tan x}{1-\tan ^{2}}}
sin ( x ± y ) = sin x cos y ± cos x sin y {\displaystyle \sin \left(x\pm y\right)=\sin x\cos y\pm \cos x\sin y}
cos ( x ± y ) = cos x cos y ∓ sin x sin y {\displaystyle \cos \left(x\pm y\right)=\cos x\cos y\mp \sin x\sin y}
tan ( x ± y ) = tan x ± tan y 1 ∓ tan x tan y {\displaystyle \tan \left(x\pm y\right)={\frac {\tan x\tan y}{1\mp \tan x\tan y}}.
Funciones hiperbólicas
Las funciones hiperbólicas son como las funciones trigonométricas, ya que tienen propiedades muy similares. Se definen en términos de la función exponencial, que se basa en la constante e.
- Seno hiperbólico:
sinh x = e x - e - x 2 = e 2 x - 1 2 e x = 1 - e - 2 x 2 e - x . {\displaystyle \sinh x={frac {e^{x}-e^{x}}{2}={frac {e^{2x}-1}{2e^{x}}={frac {1-e^{-2x}}{2e^{-x}}. }
- Coseno hiperbólico:
cosh x = e x + e - x 2 = e 2 x + 1 2 e x = 1 + e - 2 x 2 e - x . {\displaystyle \cosh x={frac {e^{x}+e^{-x}}{2}={frac {e^{2x}+1}{2e^{x}}={frac {1+e^{-2x}}{2e^{-x}}. }
- Tangente hiperbólica:
tanh x = sinh x cosh x = e x - e - x e x + e - x = e 2 x - 1 e 2 x + 1 = 1 - e - 2 x 1 + e - 2 x . {\displaystyle \tanh x={frac {\sinh x}{cosh x}}={frac {e^{x}-e^{x}}{e^{x}+e^{x}}={frac {e^{2x}-1}{e^{2x}+1}={frac {1-e^{-2x}}{1+e^{-2x}}. }
- Cotangente hiperbólica:
coth x = cosh x sinh x = e x + e - x e x - e - x = e 2 x + 1 e 2 x - 1 = 1 + e - 2 x 1 - e - 2 x , x ≠ 0. {\displaystyle \coth x={frac {\cosh x}{\sinh x}}={frac {e^{x}+e^{x}}{e^{x}-e^{x}}={frac {e^{2x}+1}{e^{2x}-1}}={frac {1+e^{-2x}}{1-e^{-2x}},\qquad x\neq 0.}
- Secante hiperbólica:
sech x = 1 cosh x = 2 e x + e - x = 2 e x e 2 x + 1 = 2 e - x 1 + e - 2 x . \frac,x={{1}{\cosh x}}={\frac {2}{e^{x}+e^{x}}={{frac {2e^{x}}{e^{2x}+1}={{frac {2e^{-x}}{1+e^{-2x}}. }
- Cosecante hiperbólica:
csch x = 1 sinh x = 2 e x - e - x = 2 e x e 2 x - 1 = 2 e - x 1 - e - 2 x , x ≠ 0. {\displaystyle \operatorname {csch} \frac {1}{sinh x}}={\frac {2}{e^{x}-e^{-x}}={\frac {2e^{x}}{e^{2x}-1}={\frac {2e^{-x}{1-e^{-2x}},\qquad x\neq 0.}
Páginas relacionadas
Buscar dentro de la enciclopedia
























