Circunferencia goniométrica
En matemáticas, un círculo unitario es un círculo con un radio de 1. La ecuación del círculo unitario es x 2 + y 2 = 1 {\displaystyle x^{2}+y^{2}=1}
. El círculo unitario está centrado en el Origen, o coordenadas (0,0). Se utiliza a menudo en Trigonometría.
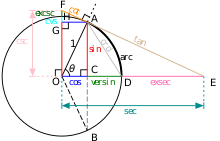
La circunferencia unitaria puede utilizarse para modelar cualquier función trigonométrica.
Funciones trigonométricas en el círculo unitario
En una circunferencia unitaria, donde t {\displaystyle t}
es el ángulo deseado, x {\displaystyle x}
e y {\displaystyle y}
pueden definirse como cos ( t ) = x {\displaystyle \cos(t)=x}
y sin ( t ) = y {\displaystyle \sin(t)=y}
. Utilizando la función del círculo unitario, x 2 + y 2 = 1 {\displaystyle x^{2}+y^{2}=1} se encuentra otra ecuación para el círculo unitario, cos 2 ( t ) + sin 2 ( t ) = 1 {\displaystyle \cos ^{2}(t)+\sin ^{2}(t)=1}
. Cuando se trabaja con funciones trigonométricas, es principalmente útil utilizar ángulos con medidas entre 0 y π 2 {\displaystyle \pi \over 2} 
radianes, o sea de 0 a 90 grados. Sin embargo, es posible tener ángulos mayores que eso. Usando el círculo unitario, se pueden encontrar dos identidades: cos ( t ) = cos ( 2 ⋅ π k + t ) {\displaystyle \cos(t)=\cos(2\cdot \pi k+t)} 
y s i n ( t ) = sin ( 2 ⋅ π k + t ) {\displaystyle sin(t)=\sin(2\cdot \pi k+t)} 
para cualquier número entero k {\displaystyle k} 
.
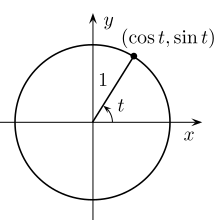
El círculo unitario puede sustituir a las variables de las funciones trigonométricas.
