Círculo: definición y propiedades — radio, diámetro, circunferencia y área

Descubre definiciones y propiedades del círculo: radio, diámetro, circunferencia, área y fórmulas con π. Explicaciones claras y ejemplos para entender y aplicar los conceptos.

Autor: Leandro Alegsa

10-02-2026 23:31

Un círculo es una figura geométrica bidimensional formada por todos los puntos que están a la misma distancia de un punto fijo llamado centro. Esa distancia constante desde el centro hasta cualquier punto del borde se llama radio.

El radio de un círculo es el segmento que va desde el centro hasta un punto de la circunferencia. Los matemáticos suelen denotar la longitud del radio con la letra r {\displaystyle r}. El centro se representa frecuentemente con la letra O {\displaystyle O} $O$ .

El diámetro (literalmente "todo el camino a través") es un segmento recto que une dos puntos opuestos de la circunferencia y pasa por el centro. Se suele usar la letra d {\displaystyle d} $d$ para su longitud. El diámetro y el radio están relacionados por la fórmula:

d = 2 r {\displaystyle d=2r} $d=2r$

La circunferencia del círculo es la curva cerrada que rodea la figura; es decir, el "borde" del círculo. Su longitud se representa con la letra C {\displaystyle C} $C$ .

La constante π

El número π (la letra griega pi) es la relación entre la longitud de la circunferencia y la del diámetro de cualquier círculo. Es decir,

π = (longitud de la circunferencia) / (longitud del diámetro). En notación simbólica, π aparece como π {\displaystyle \pi } $\pi$ .

π es un número irracional: no puede expresarse exactamente como fracción de enteros y su representación decimal es infinita y no periódica. Aproximaciones útiles son las fracciones 22 / 7 {\displaystyle 22/7} $22/7$ o 355 / 113 {\displaystyle 355/113} $355/113$ , y su valor decimal empieza aproximadamente por 3,1415926535…

Fórmulas fundamentales

Relación entre diámetro y radio: d = 2 r {\displaystyle d=2r} $d=2r$ .
Longitud de la circunferencia: C = 2 \pi r {\displaystyle C=2\pi r} (equivalente a C = \pi d {\displaystyle C=\pi d}).
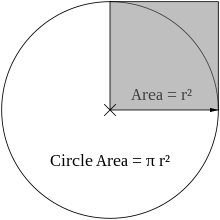
Área del círculo: el área interior se denota por A {\displaystyle A} $A$ y se calcula con la fórmula A = \pi r^2 {\displaystyle A=\pi r^2}. En palabras: el área es π multiplicado por el cuadrado del radio.

Otras cantidades relacionadas

Longitud de un arco: si el arco subtiene un ángulo central θ medido en radianes, su longitud es L = r·θ.
Área de un sector: el área de un sector circular de ángulo θ (en radianes) es A_sector = (1/2)·r²·θ.
Área de un segmento circular: es la diferencia entre el área del sector y el área del triángulo isósceles formado por los dos radios y la cuerda; su fórmula depende del ángulo θ y puede expresarse como A_segmento = (1/2)r²(θ - sin θ) (θ en radianes).
Cuerda: un segmento que une dos puntos de la circunferencia. Si la cuerda pasa por el centro se convierte en diámetro.
Tangente: una recta que toca la circunferencia en un solo punto; es perpendicular al radio que pasa por el punto de tangencia.

Ecuación en el plano cartesiano

Si el centro está en (h, k) y el radio es r, la ecuación del círculo en coordenadas cartesianas es:

(x − h)² + (y − k)² = r².

Para un círculo centrado en el origen (0,0): x² + y² = r². Esta ecuación describe todos los puntos (x,y) cuyo vector posición tiene módulo r.

Propiedades geométricas importantes

Todo radio es perpendicular a la tangente en el punto de contacto.
Los ángulos inscritos (aquellos con vértice en la circunferencia) miden la mitad del ángulo central que subtienden.
Arcos congruentes corresponden a cuerdas congruentes y a ángulos centrales congruentes.
Un diámetro divide al círculo en dos semicírculos de igual área.
Simetría: el círculo es simétrico respecto de cualquier recta que pase por su centro (simetría rotacional y reflexiva).

Ejemplos prácticos

Si r = 5 cm, entonces el diámetro es d = 2r = 10 \text{ cm}, la circunferencia es C = 2π·5 = 10π ≈ 31,416 cm y el área es A = π·5² = 25π ≈ 78,540 cm².
Si se conoce el diámetro d = 8 m, el radio es r = d/2 = 4 m; la circunferencia C = π·d ≈ 25,133 m y el área A = π·4² = 16π ≈ 50,265 m².

Aplicaciones

Los círculos aparecen en ingeniería, arquitectura, astronomía, diseño (ruedas, engranajes, rosetas), navegación (círculos máximos y menores en la esfera), en probabilidades y en teoría de ondas. Las fórmulas para longitud y área son herramientas esenciales para cálculos prácticos como diseño de piezas, cálculo de materiales y estimaciones de superficie.

Notas y recomendaciones

Para trabajar con arcos y sectores es útil expresar los ángulos en radianes: 2π rad = 360°.
Recordar que π es irracional; por tanto, en cálculos exactos se deja como π y en aproximaciones se usa su valor decimal truncado o una fracción aproximada según la precisión requerida.
Cuando se resuelven problemas concretos, verificar las unidades (metros, centímetros, etc.) y convertirlas si es necesario antes de aplicar las fórmulas.

En resumen: el círculo se caracteriza principalmente por su radio r {\displaystyle r}, su diámetro d {\displaystyle d} $d$ , la circunferencia C {\displaystyle C} $C$ y el área A {\displaystyle A} $A$ , relacionadas por las fórmulas C = 2πr (o C = πd) y A = πr², donde π {\displaystyle \pi } $\pi$ es la constante que relaciona circunferencia y diámetro.

Un círculo

El área del círculo es igual a π {\displaystyle \pi } $\pi$ veces el área del cuadrado gris.

Cálculo de π

π {\displaystyle \pi } $\pi$ puede medirse dibujando un círculo y midiendo después su diámetro ( d {\displaystyle d} $d$ ) y su circunferencia ( C {\displaystyle C} $C$ ). Esto se debe a que la circunferencia de un círculo es siempre igual a π {\displaystyle \pi } $\pi$ veces su diámetro.

π = C d {{desde el punto de vista de los medios de comunicación}} ={frac {C}{d}} $\pi ={\frac {C}{d}}$

π {\displaystyle \pi } $\pi$ también puede calcularse sólo con métodos matemáticos. La mayoría de los métodos utilizados para calcular el valor de π {\displaystyle \pi } $\pi$ tienen propiedades matemáticas deseables. Sin embargo, son difíciles de entender sin saber trigonometría y cálculo. Sin embargo, algunos métodos son bastante sencillos, como esta forma de la serie de Gregory-Leibniz:

π = 4 1 - 4 3 + 4 5 - 4 7 + 4 9 - 4 11 ... {\displaystyle \pi ={frac {4}{1}}-{frac {4}{3}}+{frac {4}{5}}-{frac {4}{7}}+{frac {4}{9}}-{frac {4}{11}{puntos}} $\pi ={\frac {4}{1}}-{\frac {4}{3}}+{\frac {4}{5}}-{\frac {4}{7}}+{\frac {4}{9}}-{\frac {4}{11}}\,\ldots$

Mientras que esa serie es fácil de escribir y calcular, no es fácil ver por qué es igual a π {\displaystyle \pi } $\pi$ . Una forma mucho más fácil de aproximarse es dibujar un círculo imaginario de radio r {\displaystyle r} centrado en el origen. Entonces cualquier punto ( x {\displaystyle x} , y {\displaystyle y} ) cuya distancia d {\displaystyle d} $d$ al origen sea menor que r {\displaystyle r} , calculada por el teorema de Pitágoras, estará dentro del círculo:

d = x 2 + y 2 {\displaystyle d={sqrt {x^{2}+y^{2}}}} $d={\sqrt {x^{2}+y^{2}}}$

Encontrar un conjunto de puntos dentro del círculo permite estimar el área A {\displaystyle A} $A$ del círculo, por ejemplo, utilizando coordenadas enteras para un gran r {\displaystyle r} . Como el área A {\displaystyle A} $A$ de un círculo es π {\displaystyle \pi } $\pi$ veces el radio al cuadrado, π {\displaystyle \pi } $\pi$ puede aproximarse utilizando la siguiente fórmula:

π = A r 2 {\displaystyle \pi ={frac {A}{r^{2}}}} $\pi ={\frac {A}{r^{2}}}$

Calcular el área, la circunferencia, el diámetro y el radio de un círculo

Área

Utilizando su radio: A = π r 2 {\displaystyle A=\pi r^{2}} $A=\pi r^{2}$

Utilizando su diámetro: A = π d 2 4 {\displaystyle A={\frac {\pi d^{2}{4}} $A={\frac {\pi d^{2}}{4}}$

Utilizando su circunferencia: A = C 2 4 π {\displaystyle A={\frac {C^{2}{4\pi }} $A={\frac {C^{2}}{4\pi }}$

Circunferencia

Utilizando su diámetro: C = π d {\N-estilo de la pantalla C=\pi d} $C=\pi d$

Utilizando su radio: C = 2 π r {\displaystyle C=2\pi r} $C=2\pi r$

Utilizando su área: C = 2 π A {\displaystyle C=2{cuadrado de A}} $C=2{\sqrt {\pi A}}$

Diámetro

Utilizando su radio: d = 2 r {\displaystyle d=2r} $d=2r$

Utilizando su circunferencia: d = C π {\displaystyle d={\frac {C}{pi }} $d={\frac {C}{\pi }}$

Utilizando su área: d = 2 A π {\displaystyle d=2{sqrt {\frac {A}{pi }}}} $d=2{\sqrt {\frac {A}{\pi }}}$

Radio

Utilizando su diámetro: r = d 2 {\displaystyle r={frac {d}{2}} $r={\frac {d}{2}}$

Utilizando su circunferencia: r = C 2 π {\displaystyle r={\frac {C}{2\pi }} $r={\frac {C}{2\pi }}$

Utilizando su área: r = A π {\displaystyle r={sqrt {\frac {A}{pi }}}} $r={\sqrt {\frac {A}{\pi }}}$

Páginas relacionadas

Semicírculo
Esfera
La cuadratura del círculo
Pi
Pi (letra)
Tau

Preguntas y respuestas

P: ¿Qué es un círculo?

R: Un círculo es una forma redonda y bidimensional. Todos los puntos del borde del círculo están a la misma distancia del centro.

P: ¿Qué utilizan los matemáticos para representar la longitud del radio de un círculo?

R: Los matemáticos utilizan la letra r para la longitud del radio de un círculo.

P: ¿Qué se escribe como O en los círculos?

R: El centro de un círculo se suele escribir como O.

P: ¿Qué longitud tiene el diámetro de un círculo?

R: El diámetro (que significa "todo el camino") de un círculo es una línea recta que va de un lado al opuesto y pasa por el centro del círculo. Es igual al doble de su radio (d es igual a 2 veces r).

P: ¿Qué letra utilizan los matemáticos para representar la circunferencia?

R: Los matemáticos utilizan la C para la circunferencia, que significa "todo alrededor".

P: ¿Cómo podemos calcular el área dentro de un círculo?

R: El área, A, dentro de un círculo se puede calcular multiplicando su radio por sí mismo y luego multiplicado por ً (A es igual a ً por r por r).

Buscar dentro de la enciclopedia