Número π | constante matemática que es la relación entre la circunferencia de un círculo y su diámetro
El número π (/paɪ/) es una constante matemática que es la relación entre la circunferencia de un círculo y su diámetro. Esto produce un número, y ese número es siempre el mismo. Sin embargo, el número es bastante extraño. El número comienza como 3,141592653589793... y continúa sin fin. Los números como éste se llaman números irracionales.
El diámetro es la mayor cuerda que puede caber dentro de un círculo. Pasa por el centro del círculo. La distancia alrededor de un círculo se conoce como la circunferencia. Aunque el diámetro y la circunferencia son diferentes para distintos círculos, el número pi permanece constante: su valor nunca cambia. Esto se debe a que la relación entre la circunferencia y el diámetro es siempre la misma.
Pi es una cadena interminable de números
Fundamentos
Definición
π se define comúnmente como la relación entre la circunferencia C de un círculo y su diámetro d:
Valor aproximado
Pi se escribe a menudo como π, o la letra griega π como atajo. Pi es también un número irracional, lo que significa que no puede escribirse como una fracción ( 
), donde "a" y "b" son números enteros (números enteros). Esto significa básicamente que los dígitos de pi que están a la derecha del decimal se eternizan sin repetirse en un patrón, y que es imposible escribir el valor exacto de pi como un número. Pi sólo puede ser aproximado, o medido a un valor lo suficientemente cercano para fines prácticos.
Un valor cercano a pi es 3,141592653589793238462643... Una aproximación común de la fracción de pi es 
, que da aproximadamente 3,14285714. Esta aproximación se aleja un 0,04% del verdadero valor de pi. Aunque esta aproximación se acepta para la mayor parte de su uso en la vida real, la fracción 
es más precisa (da aproximadamente 3,14159292), y puede utilizarse cuando se necesita un valor más cercano a pi. Se pueden utilizar ordenadores para obtener mejores aproximaciones de pi.
En marzo de 2019, Emma Haruka Iwao calculó el valor de pi en 31,4 billones de dígitos.
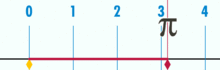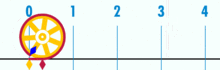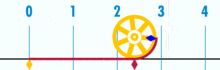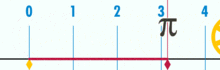
Un diagrama que muestra cómo se puede encontrar π utilizando un círculo con un diámetro de uno. La circunferencia de este círculo es π.
La circunferencia de un círculo es algo más de tres veces mayor que su diámetro. La proporción exacta se llama π.
Historia
Los matemáticos conocen pi desde hace miles de años, porque llevan el mismo tiempo trabajando con círculos. Civilizaciones tan antiguas como la babilónica han sido capaces de aproximar pi a muchos dígitos, como la fracción 25/8 y 256/81. La mayoría de los historiadores creen que los antiguos egipcios no tenían el concepto de π, y que la correspondencia es una coincidencia.
La primera referencia escrita a pi data del año 1900 a.C. Alrededor del 1650 a.C., el egipcio Ahmes dio un valor en el Papiro Rhind. Los babilonios fueron capaces de encontrar que el valor de pi era ligeramente superior a 3, simplemente haciendo un gran círculo y luego pegando un trozo de cuerda en la circunferencia y el diámetro, tomando nota de sus distancias, y luego dividiendo la circunferencia por el diámetro.
El conocimiento del número pi pasó a Europa y a manos de los hebreos, que dieron importancia al número en una sección de la Biblia llamada el Antiguo Testamento. Después de esto, la forma más común de intentar encontrar pi era dibujar una forma de muchos lados dentro de un círculo cualquiera, y utilizar el área de la forma para encontrar pi. El filósofo griego Arquímedes, por ejemplo, utilizó una forma de polígono que tenía 96 lados para encontrar el valor de pi, pero los chinos en el año 500 de la era cristiana fueron capaces de utilizar un polígono con 16.384 lados para encontrar el valor de pi. Los griegos, como Anaxágoras de Clazomena, también se ocuparon de averiguar otras propiedades del círculo, como la forma de hacer cuadrados de círculos y la cuadratura del número pi. Desde entonces, muchas personas han tratado de averiguar valores cada vez más exactos de pi.
| Una historia de pi | ||
| Filósofo | Fecha | Aproximación |
| alrededor de 150 CE | 3.1416 | |
| Zu Chongzhi | 430-501 CE | 3.1415929203 |
| al-Khwarizmi | alrededor del año 800 CE | 3.1416 |
| al-Kashi | alrededor de 1430 | 3.14159265358979 |
| Viète | 1540-1603 | 3.141592654 |
| Roomen | 1561-1615 | 3.14159265358979323 |
| Van Ceulen | alrededor de 1600 | 3.14159265358979323846264338327950288 |
En el siglo XVI, aparecieron formas cada vez mejores de hallar pi, como la complicada fórmula que desarrolló el jurista francés François Viète. El primer uso del símbolo griego "π" fue en un ensayo escrito en 1706 por William Jones.
Un matemático llamado Lambert también demostró en 1761 que el número pi era irracional, es decir, que no puede escribirse como una fracción según los estándares normales. Otro matemático llamado Lindeman también pudo demostrar en 1882 que pi formaba parte del grupo de números conocidos como trascendentales, que son números que no pueden ser la solución de una ecuación polinómica.
Pi también puede utilizarse para calcular muchas otras cosas además de los círculos. Las propiedades de pi han permitido que se utilice en muchas otras áreas de las matemáticas además de la geometría, el estudio de las formas. Algunas de estas áreas son el análisis complejo, la trigonometría y las series.
Pi en la vida real
Existen diferentes formas de calcular muchos dígitos de π, pero su utilidad es limitada.
A veces se puede utilizar Pi para calcular el área o la circunferencia de cualquier círculo. Para hallar la circunferencia de un círculo, utilice la fórmula C (circunferencia) = π × (diámetro). Para hallar el área de un círculo, utilice la fórmula π (radio²). Esta fórmula se escribe a veces como 
, donde r es la variable del radio de cualquier círculo y A es la variable del área de ese círculo.
Calcular la circunferencia de un círculo con un error de 1 mm:
- Se necesitan 4 dígitos para un radio de 30 metros
- 10 dígitos para un radio igual al de la tierra
- 15 dígitos para un radio igual a la distancia de la tierra al sol.
- 20 dígitos para un radio igual a la distancia de la tierra a Polaris.
La gente suele celebrar el 14 de marzo como el Día de Pi, porque el 14 de marzo también se escribe 3/14, que representa los tres primeros números 3,14 en la aproximación de pi. El día de Pi comenzó durante el año 2001.
Páginas relacionadas
- Lista de números
- Números irracionales
- Raíz cuadrada de 2
- Relación áurea
- E (constante matemática)
- La cuadratura del círculo
- Número trascendental
Preguntas y respuestas
P: ¿Qué es el número נ?
R: נ es una constante matemática que es la relación entre la circunferencia de un círculo y su diámetro.
P: ¿Qué produce esto?
R: Esto produce un número, y ese número es siempre el mismo.
P: ¿Cómo empieza este número?
R: El número comienza como 3,141592653589793... y continúa sin fin.
P: ¿Qué tipo de números son estos?
R: Estos números se llaman números irracionales.
P: ¿Qué es el diámetro de un círculo?
R: El diámetro de un círculo es la mayor cuerda que puede caber dentro de él, pasando por su centro.
P: ¿Qué es la circunferencia de un círculo? R: La distancia alrededor de un círculo se conoce como su circunferencia.
P: ¿Permanece pi constante independientemente de los diferentes círculos? R: Sí, pi permanece constante independientemente de los diferentes círculos porque la relación entre su circunferencia y su diámetro siempre es la misma.
