Desigualdad matemática

Trabajar con desigualdades

La desigualdad en matemáticas es cuando dos soluciones o respuestas se comparan por mayor que o menor que. Es cuando las dos o aún muchas soluciones que se comparan no son de igual cantidad. Resolver una desigualdad significa encontrar sus soluciones. Cuando se sustituye un número a una variable y el enunciado es verdadero, entonces es una solución. Cuando se sustituye un número por una variable y el enunciado no es verdadero, entonces, el número no es una solución del enunciado.

La desigualdad es encontrar una solución a una variable dada. Es encontrar un orden relativo de un conjunto. Las desigualdades tienen muchas soluciones, pero hay que encontrar las soluciones reales. La desigualdad es resolver números reales. La forma correcta de leer la desigualdad es de izquierda a derecha, igual que las otras ecuaciones, pero la única diferencia es que tienen reglas diferentes para cada ecuación.

Por ejemplo, x+4>12, donde x es un número real. En primer lugar, una persona necesita encontrar la x y necesita saber si es una solución. La respuesta será x>8 y es una afirmación verdadera. Esta expresión se refiere a la ubicación de x dentro del conjunto de números reales. Una recta numérica es una forma de mostrar la ubicación en relación con todos los demás números reales.(Ver figura Desigualdad 1)

Desigualdad 1 Esta es la solución de la ecuación x+4>12

Diferentes tipos de desigualdades

Hay cinco tipos diferentes de desigualdades:

1. La primera son las inecuaciones lineales que son una desigualdad que diferencia las expresiones por menor o igual que, menor que o mayor que, mayor que. Es una que si sustituimos la desigualdad por la relación de igualdad, entonces el resultado será una ecuación lineal.
2. La segunda son las combinaciones de inecuaciones que son para satisfacer las inecuaciones, hay que tener un número en los conjuntos solución para que los números satisfagan las inecuaciones van a ser los valores en el cruce de los dos conjuntos solución.
3. La tercera son las desigualdades que implican valores absolutos, lo que significa que los valores pueden reformularse como combinaciones de desigualdades que implicarán valores absolutos.
4. La cuarta se llama desigualdades polinómicas significa que es continua, quiere decir que sus gráficas no tienen saltos ni rupturas.
5. Por último, pero no menos importante, son las inecuaciones racionales, lo que significa que es la forma de uno de los polinomios dividido por un polinomio. En otras palabras, las gráficas de las funciones racionales no tienen ninguna ruptura ni representan en los ceros del denominador.

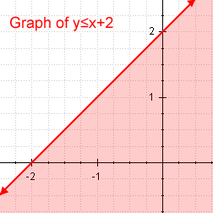
Desigualdad lineal Ejemplo de desigualdad lineal


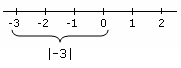
valor absoluto Ejemplo que muestra el valor absoluto

Cuatro formas de resolver desigualdades

Hay cuatro formas de resolver ecuaciones cuadráticas:

1. La regla número uno es que tienes que sumar o restar el mismo número en ambos lados.
2. La regla número dos es que hay que desplazar los lados y cambiar la posición del signo de la desigualdad.
3. La regla número tres es que hay que multiplicar.
4. La regla número cuatro consiste en dividir el mismo número positivo o negativo entre ambos lados. Pero, sólo puedes usarlas en problemas de desigualdades fáciles.

Además, se necesitan dos pasos para resolver una desigualdad. El primero es simplificar utilizando el recíproco de la suma o la resta. El segundo es simplificar más utilizando el recíproco de la multiplicación o la división. Cuando estés multiplicando o dividiendo una desigualdad por un número negativo, recuerda girar el símbolo de la desigualdad.

Un ejemplo de adición de desigualdades.


ejemplo de multiplicación de la desigualdad

Ejemplos de cómo resolver desigualdades

La desigualdad es un enunciado matemático que explica que los dos valores no son iguales y diferentes. La ecuación ab significa que a no es igual a b. La desigualdad es igual a cualquier ecuación pero la única diferencia es que la desigualdad no utiliza un signo de igualdad sino que utiliza símbolos. La desigualdad b>a representa que b es mayor que a. Los límites de velocidad, la marca y otros utilizan la desigualdad para expresarlos.

Cuando se resuelve una inecuación es necesario que el enunciado sea verdadero. Cuando se divide o multiplica una desigualdad con un número negativo en ambos lados, la afirmación es falsa. Cuando un número es positivo, no es necesario invertir el símbolo. La desigualdad consiste en hacer una afirmación verdadera.

Por ejemplo, comience con una afirmación verdadera -6y<-12. Cuando ambos lados se dividen por -6 el resultado será y< 2. En este enunciado hay que invertir el símbolo para tener un enunciado verdadero, y>2 es la respuesta correcta. En la recta numérica (ver figura Desigualdad 2), un círculo cerrado sombreado señala que está incluido en el conjunto de soluciones. Un círculo abierto indica que no está incluido en el conjunto de soluciones.

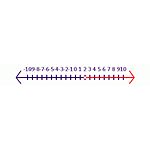
Desigualdad 2 Solución de la ecuación -6y<-12

Páginas relacionadas

• Igualdad (matemáticas)
• Ecuación