Trigonometría

La trigonometría (del griego trigonon = tres ángulos y metron = medida) es una parte de las matemáticas elementales que trata de los ángulos, los triángulos y las funciones trigonométricas como el seno (abreviado sin), el coseno (abreviado cos) y la tangente (abreviado tan). Tiene cierta relación con la geometría, aunque no se sabe exactamente cuál es esa relación; para algunos, la trigonometría es sólo una sección de la geometría.

Resumen y definiciones

La trigonometría utiliza un gran número de palabras específicas para describir las partes de un triángulo. Algunas de las definiciones en trigonometría son:

Triángulo rectángulo - Un triángulo rectángulo es un triángulo que tiene un ángulo que es igual a 90 grados. (Un triángulo no puede tener más de un ángulo recto) Las razones trigonométricas estándar sólo pueden utilizarse en triángulos rectángulos.
Hipotenusa - La hipotenusa de un triángulo es el lado más largo y el lado opuesto al ángulo recto. Por ejemplo, para el triángulo de la derecha, la hipotenusa es el lado c.
Opuesto de un ángulo - El lado opuesto de un ángulo es el lado que no se cruza con el vértice del ángulo. Por ejemplo, el lado a es el opuesto del ángulo A en el triángulo de la derecha.
Adyacente de un ángulo - El lado adyacente de un ángulo es el lado que interseca el vértice del ángulo pero no es la hipotenusa. Por ejemplo, el lado b es adyacente al ángulo A en el triángulo de la derecha.

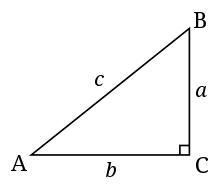
Un triángulo rectángulo estándar. C es el ángulo recto en esta imagen

Relaciones trigonométricas

Hay tres razones trigonométricas principales para los triángulos rectángulos, y tres recíprocas de esas razones. En total hay 6 razones. Son:

Seno (sin) - El seno de un ángulo es igual a la Hipotenusa opuesta {\displaystyle {{text{Opposite}} \over {\text{Hypotenuse}}}} ${{\text{Opposite}} \over {\text{Hypotenuse}}}$
Coseno (cos) - El coseno de un ángulo es igual a la Hipotenusa Adyacente {{displaystyle}}. \over {\text{Hypotenuse}}}} ${{\text{Adjacent}} \over {\text{Hypotenuse}}}$
Tangente (tan) - La tangente de un ángulo es igual al opuesto adyacente. \over {\text{Adjacent}}}} ${{\text{Opposite}} \over {\text{Adjacent}}}$

Los recíprocos de estos ratios son:

Cosecante (csc) - La cosecante de un ángulo es igual a la Hipotenusa Opuesta {\displaystyle {\text{Hipotenusa}} \text {\text{Opuesta}}}}} ${{\text{Hypotenuse}} \over {\text{Opposite}}}$ o csc θ = 1 sin θ {\displaystyle \csc \theta ={1 \\text{sin \theta}} $\csc \theta ={1 \over \sin \theta }$

Secante (sec) - La secante de un ángulo es igual a la Hipotenusa Adyacente {\displaystyle {{text{Hipotenusa}} \text{Adjacent}}}} ${{\text{Hypotenuse}} \over {\text{Adjacent}}}$ o sec θ = 1 cos θ {\displaystyle \sec \theta ={1 \\\\cocos \theta }} $\sec \theta ={1 \over \cos \theta }$

Cotangente (cot) - La cotangente de un ángulo es igual al opuesto adyacente {\displaystyle {{text{Adjacent}} \text {\text{Opuesto}}}} ${{\text{Adjacent}} \over {\text{Opposite}}}$ o cot θ = 1 tan θ {\displaystyle \cot \theta ={1 \text{tan \theta }} $\cot \theta ={1 \over \tan \theta }$

Los alumnos suelen utilizar una mnemotecnia para recordar esta relación. Las relaciones seno, coseno y tangente en un triángulo rectángulo pueden recordarse representándolas como cadenas de letras, como SOH-CAH-TOA:

Seno = Opuesto ÷ Hipotenusa

Coseno = Adyacente ÷ Hipotenusa

Tangente = Opuesto ÷ Adyacente

Utilizando la trigonometría

Con los senos y cosenos se puede responder a prácticamente todas las preguntas sobre triángulos. Esto se llama "resolver" el triángulo. Se pueden resolver los ángulos y lados restantes de cualquier triángulo en cuanto se conozcan dos lados y su ángulo incluido o dos ángulos y un lado o tres lados. Estas leyes son útiles en todas las ramas de la geometría, ya que todo polígono puede describirse como una combinación de triángulos.

La trigonometría también es vital en la topografía, en el análisis vectorial y en el estudio de las funciones periódicas.

También existe la trigonometría esférica, que se ocupa de la geometría esférica. Se utiliza para cálculos en astronomía, geodesia y navegación.

Leyes de trigonometría

Ley de los senos

a Sin A = b Sin B = c Sin C {\displaystyle {{text{a}} \{{texto}}sobre {{sin A}}={texto}}b} \{{text}} sobre {{texto}} de pecado B}} = {{texto}} de pecado C encima {\text{Sin C}}= {\text{Sin C}} ${{\text{a}} \over {\text{Sin A}}}={{\text{b}} \over {\text{Sin B}}}={{\text{c}} \over {\text{Sin C}}}$

Ley de los Cosenos

a 2 = b 2 + c 2 - 2 b c cos ( A ) {\displaystyle a^{2}=b^{2}+c^{2}-2bc\cos(A)} $a^{2}=b^{2}+c^{2}-2bc\cos(A)$

Ley de las Tangentes

a - b a + b = tan ( 1 2 ( A - B ) ) tan ( 1 2 ( A + B ) ) {\displaystyle {\frac {a-b}{a+b}}= {\frac {\tan({\frac {1}{2}(A-B))}{{tan({\frac {1}{2}(A+B))}} ${\frac {a-b}{a+b}}={\frac {\tan({\frac {1}{2}}(A-B))}{\tan({\frac {1}{2}}(A+B))}}$