Teorema de Pitágoras | afirmación sobre los lados de un triángulo rectángulo

En matemáticas, el teorema de Pitágoras o teorema de Pitágoras es una afirmación sobre los lados de un triángulo rectángulo.

Uno de los ángulos de un triángulo rectángulo es siempre igual a 90 grados. Este ángulo es el ángulo recto. Los dos lados próximos al ángulo recto se llaman catetos y el otro lado se llama hipotenusa. La hipotenusa es el lado opuesto al ángulo recto y es siempre el lado más largo.

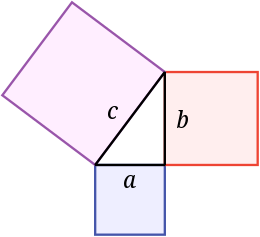
Teorema de Pitágoras La suma de las áreas de los dos cuadrados de los catetos (a y b) es igual al área del cuadrado de la hipotenusa (c).

Afirmación de la teoría

El teorema de Pitágoras dice que el área de un cuadrado de la hipotenusa es igual a la suma de las áreas de los cuadrados de los catetos. En esta imagen, el área del cuadrado azul sumada al área del cuadrado rojo hace el área del cuadrado morado. Su nombre se debe al matemático griego Pitágoras:

Si las longitudes de los catetos son a y b, y la longitud de la hipotenusa es c, entonces, a 2 + b 2 = c 2 {\displaystyle a^{2}+b^{2}=c^{2}}. $a^{2}+b^{2}=c^{2}$ .

Tipos de pruebas

Hay muchas pruebas diferentes de este teorema. Se dividen en cuatro categorías:

Las basadas en relaciones lineales: las pruebas algebraicas.
Las basadas en la comparación de áreas: las pruebas geométricas.
Los basados en la operación vectorial.
Las basadas en la masa y la velocidad: las pruebas dinámicas.

Prueba

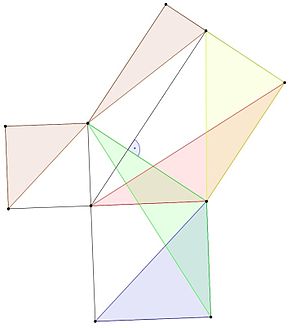
Una de las pruebas del teorema de Pitágoras fue encontrada por un matemático griego, Eudoxo de Cnidus.

La prueba utiliza tres lemas:

Los triángulos con la misma base y altura tienen la misma área.
Un triángulo que tiene la misma base y altura que un lado de un cuadrado tiene la misma área que la mitad del cuadrado.
Los triángulos con dos lados congruentes y un ángulo congruente son congruentes y tienen la misma área.

La prueba es:

El triángulo azul tiene la misma área que el verde, porque tiene la misma base y altura (lema 1).
Los triángulos verde y rojo tienen ambos dos lados iguales a los lados de los mismos cuadrados, y un ángulo igual a un ángulo recto (un ángulo de 90 grados) más un ángulo de un triángulo, por lo que son congruentes y tienen la misma área (lema 3).
Las áreas de los triángulos rojo y amarillo son iguales porque tienen las mismas alturas y bases (lema 1).
El área del triángulo azul es igual al área del triángulo amarillo, porque

A b l u e = A g r e e n = A r e d = A y e l l o w {{color azul}A_{azul}}={color verde}A_{verde}}={color rojo}A_{rojo}}={color amarillo}A_{amarillo}} ${\color {blue}A_{blue}}={\color {green}A_{green}}={\color {red}A_{red}}={\color {yellow}A_{yellow}}$

Los triángulos marrones tienen la misma área por las mismas razones.
El azul y el marrón tienen cada uno la mitad del área de un cuadrado más pequeño. La suma de sus áreas es igual a la mitad del área del cuadrado mayor. Por ello, las mitades de las áreas de los cuadrados pequeños son iguales a la mitad del área del cuadrado mayor, por lo que su área es la misma que la del cuadrado mayor.

Prueba mediante triángulos semejantes

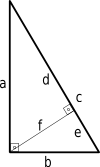
Podemos obtener otra prueba del teorema de Pitágoras utilizando triángulos semejantes.

d a = a c ⇒ a 2 = d c ( 1 ) {\displaystyle {\frac {d}{a}}={frac {a}{c}}cuadrado \frac {a^{2}}={dc}{cuadrado (1)} ${\frac {d}{a}}={\frac {a}{c}}\quad \Rightarrow \quad {a^{2}}={dc}\quad (1)$

e b = b c ⇒ b 2 = e c ( 2 ) {\displaystyle {\frac {e}{b}}={frac {b}{c}}cuadrado \frac {b^{2}}={ec}{cuadrado (2)} ${\frac {e}{b}}={\frac {b}{c}}\quad \Rightarrow \quad {b^{2}}={ec}\quad (2)$

A partir de la imagen, sume las ecuaciones (1) y (2):

a 2 + b 2 = d c + e c ⇒ a 2 + b 2 = c ( d + e ) ⇒

${a^{2}}+{b^{2}}={dc+ec}\quad \Rightarrow a^{2}+b^{2}=c(d+e)\quad \Rightarrow a^{2}+b^{2}=c(c)$

Y nos quedamos con:

c 2 = a 2 + b 2 . {\displaystyle c^{2}=a^{2}+b^{2}\}.} $c^{2}=a^{2}+b^{2}\,\!.$

Triples pitagóricos

Los triples pitagóricos o tripletes son tres números enteros que se ajustan a la ecuación a 2 + b 2 = c 2 {\displaystyle a^{2}+b^{2}=c^{2}}. $a^{2}+b^{2}=c^{2}$ .

El triángulo con lados de 3, 4 y 5 es un ejemplo bien conocido. Si a=3 y b=4, entonces 3 2 + 4 2 = 5 2 {\displaystyle 3^{2}+4^{2}=5^{2}} $3^{2}+4^{2}=5^{2}$ porque 9 + 16 = 25 {\displaystyle 9+16=25} $9+16=25$ . Esto también puede mostrarse como 3 2 + 4 2 = 5. {\displaystyle {\sqrt {3^{2}+4^{2}}=5.} ${\sqrt {3^{2}+4^{2}}}=5.$

El triángulo tres-cuatro-cinco funciona para todos los múltiplos de 3, 4 y 5. En otras palabras, números como 6, 8, 10 o 30, 40 y 50 también son triples pitagóricos. Otro ejemplo de triple es el triángulo 12-5-13, porque 12 2 + 5 2 = 13 {\displaystyle {\sqrt {12^{2}+5^{2}}=13} ${\sqrt {12^{2}+5^{2}}}=13$ .

Un triple pitagórico que no es múltiplo de otros triples se llama triple pitagórico primitivo. Cualquier triple pitagórico primitivo se puede hallar mediante la expresión ( 2 m n , m 2 - n 2 , m 2 + n 2 ) {\displaystyle (2mn,m^{2}-n^{2},m^{2}+n^{2})} $(2mn,m^{2}-n^{2},m^{2}+n^{2})$ , pero deben satisfacerse las siguientes condiciones. Imponen restricciones a los valores de m {\displaystyle m} y n {\displaystyle n} .

m {\displaystyle m} y n {\displaystyle n} son números enteros positivos
m {\displaystyle m} y n {\displaystyle n} no tienen factores comunes excepto 1
m {\displaystyle m} y n {\displaystyle n} tienen paridad opuesta. m {\displaystyle m} y n {\displaystyle n} tienen paridad opuesta cuando m {\displaystyle m} es par y n {\displaystyle n} es impar, o m {\displaystyle m} es impar y n {\displaystyle n} es par.
m > n {\desde el estilo m>n} $m>n$ .

Si se cumplen las cuatro condiciones, entonces los valores de m {\displaystyle m} y n {\displaystyle n} crean un triple pitagórico primitivo.

m = 2 {\displaystyle m=2} $m=2$ y n = 1 {\displaystyle n=1} $n=1$ crean un triple pitagórico primitivo. Los valores satisfacen las cuatro condiciones. 2 m n = 2 × 2 × 1 = 4 {\displaystyle 2mn=2\times 2\times 1=4} $2mn=2\times 2\times 1=4$ , m 2 - n 2 = 2 2 - 1 2 = 4 - 1 = 3 {\displaystyle m^{2}-n^{2}=2^{2}-1^{2}=4-1=3} $m^{2}-n^{2}=2^{2}-1^{2}=4-1=3$ y m 2 + n 2 = 2 + 1 2 = 4 + 1 = 5 {\displaystyle m^{2}+n^{2}=2^{2}+1^{2}=4+1=5} $m^{2}+n^{2}=2^{2}+1^{2}=4+1=5$ , por lo que se crea el triple ( 3 , 4 , 5 ) {\displaystyle (3,4,5)} $(3,4,5)$ .

Preguntas y respuestas

P: ¿Qué es el teorema de Pitágoras?

R: El teorema de Pitágoras es una afirmación sobre los lados de un triángulo rectángulo.

P: ¿Qué ángulo es siempre igual a 90 grados en un triángulo rectángulo?

R: Uno de los ángulos de un triángulo rectángulo es siempre igual a 90 grados, lo que se denomina ángulo recto.

P: ¿Cómo se llaman los dos lados junto al ángulo recto?

R: Los dos lados próximos al ángulo recto se llaman catetos.

P: ¿Cómo se llama el lado opuesto al ángulo recto?

R: El lado opuesto al ángulo recto se llama hipotenusa y es siempre el lado más largo.

P: ¿Existe una ecuación para calcular este teorema?

R: Sí, existe una ecuación para calcular este teorema que dice que "el cuadrado de la longitud de la hipotenusa es igual a la suma de los cuadrados de las longitudes de los otros dos lados".

P: ¿Todos los triángulos con ángulos de 90 grados se consideran triángulos "rectos"?

R: No, no todos los triángulos con ángulos de 90 grados se consideran triángulos "rectos"; sólo aquellos en los que un lado (hipotenusa) es más largo que los otros dos lados y forma un ángulo de 90 grados en su extremo pueden clasificarse como triángulos "rectos".