Función matemática

En matemáticas, una función es un objeto matemático que produce una salida, cuando se le da una entrada (que puede ser un número, un vector, o cualquier cosa que pueda existir dentro de un conjunto de cosas).

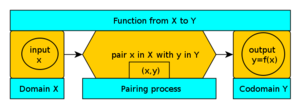
Así que una función es como una máquina, que toma un valor de x y devuelve una salida y. El conjunto de todos los valores que puede tener x se llama dominio, y el conjunto que contiene todos los valores que puede tener y se llama codominio. Una función se denota a menudo con letras cursivas, como f {\displaystyle f} , g {\displaystyle g} , h {\displaystyle h} $h$ .

Si esto ocurre, entonces decimos que y es una función de x, y escribimos y = f ( x ) {\displaystyle y=f(x)} $y=f(x)$ . Aquí, f {\displaystyle f} es el nombre de la función, y se escribe f : X → Y {\displaystyle f:X\to Y} (función de X a Y) para representar las tres partes de la función: el dominio (X), el codominio (Y) y el proceso de emparejamiento (la flecha).

Un ejemplo de función es f ( x ) = x + 1 {\displaystyle f(x)=x+1} $f(x)=x+1$ . Uno da un número natural x {\displaystyle x} como entrada, y obtiene un número natural y {\displaystyle y} , que es x + 1 {\displaystyle x+1} $x+1$ . Por ejemplo, dar 3 como entrada a f {\displaystyle f} da como resultado una salida de 4.

Una función no tiene por qué ser una ecuación. La idea principal es que las entradas y salidas se emparejen de alguna manera, aunque el proceso pueda ser muy complicado.

Metáforas

Tablas

Las entradas y salidas se pueden poner en una tabla como la de la imagen; esto es fácil si no hay demasiados datos.

Gráficos

En la imagen, se puede ver que tanto 2 como 3 han sido emparejados con c; esto no está permitido en el otro sentido, ya que 2 no podría dar salida a c y d al mismo tiempo (cada entrada sólo puede tener una salida). El conjunto de f ( x ) {\displaystyle f(x)} f(x) (c y d en la imagen) suele llamarse conjunto imagen de f {displaystyle f} , y el conjunto imagen puede ser todo el codominio o uno de sus subconjuntos. Se puede decir que el conjunto imagen de un subconjunto A del dominio es f(A). Si las entradas y salidas tienen un orden, entonces es fácil trazarlas en un gráfico:

De este modo, la imagen viene sobre la imagen del conjunto A.

Historia

En la década de 1690, Gottfried Leibniz y Johann Bernoulli utilizaron la palabra "función" en letras entre ellos, por lo que el concepto moderno comenzó al mismo tiempo que el cálculo.

En 1748, Leonhard Euler dio la siguiente definición de función:

"Una función de una cantidad variable es una expresión analítica compuesta de cualquier manera por la cantidad variable y números o cantidades constantes".

y luego en 1755:

"Si algunas cantidades dependen de tal manera de otras cantidades que si estas últimas se modifican las primeras sufren cambios, entonces las primeras cantidades se llaman funciones de las segundas. Esta definición se aplica de forma bastante amplia e incluye todas las formas en las que una cantidad puede estar determinada por otra. Por lo tanto, si x denota una cantidad variable, entonces todas las cantidades que dependen de x de alguna manera, o están determinadas por ella, se llaman funciones de x".

Normalmente, se atribuye a Peter Dirichlet la primera definición moderna de función (formulada en 1837). Se utiliza a menudo en las escuelas hasta la segunda mitad del siglo XX:

"y es una función de una variable x, definida en el intervalo a < x < b, si a todo valor de la variable x en este intervalo le corresponde un valor definido de la variable y. Además, es irrelevante de qué manera se establece esta correspondencia".

En 1939, Bourbaki generalizó la definición de Dirichlet, y dio una versión teórica de conjuntos de la definición como una correspondencia entre entradas y salidas; esto se utilizó en las escuelas desde aproximadamente 1960.

Finalmente, en 1970, Bourbaki dio la definición moderna como un triple f = ( X , Y , F ) {\displaystyle f=(X,Y,F)} , con F ⊂ X × Y , ( x , f ( x ) ) ∈ $F\subset X\times Y,(x,f(x))\in F$ (es decir, f : X → Y {\displaystyle f:X\to Y} y F = ( x , f ( x ) ∣ x ∈ X , f ( x ) ∈ Y $F=\{(x,f(x))\mid x\in X,f(x)\in Y\}$ ). $X se$ llama el dominio de $f$ , $Y$ su codominio, y $F$ su gráfica. El conjunto de todos los elementos de la forma $f (x)$ , donde $x$ abarca los elementos del dominio $X$ , se llama imagen de $f.$ La imagen de una función es un subconjunto de su codominio y puede no coincidir con él.

Tipos de funciones

Funciones elementales - Las funciones que se suelen estudiar en la escuela: fracciones, raíces cuadradas, las funciones seno, coseno y tangente y algunas otras funciones.
Funciones no elementales - La mayoría de ellas utilizan operaciones que no aprendemos en la escuela (como + o -, o potencias). Muchas integrales, por ejemplo, son no elementales.
Funciones inversas - Funciones que deshacen otra función. Por ejemplo: si F(x) es la inversa de f(x)=y, entonces F(y)=x. No todas las funciones tienen inversas.
Funciones especiales: Funciones que tienen nombre. Entre ellas se encuentran las funciones trigonométricas como el seno, el coseno y la tangente. Las funciones como f(x)=3x (tres veces x) no se llaman funciones especiales. Las funciones especiales pueden ser elementales, no elementales o inversas.

Páginas relacionadas

Función constante
Función continua
Composición de la función
Funciones especiales

Función gamma
Función matricial

Función lineal
Lucy Joan Slater - Matemática británica que estudió sobre las funciones matemáticas
MATLAB, Wolfram Mathematica - software para calcular funciones matemáticas
Relación (matemáticas)

Preguntas y respuestas

P: ¿Qué es una función en matemáticas?

R: Una función en matemáticas es un objeto que produce una salida cuando se le da una entrada, que puede ser un número, un vector o cualquier cosa que pueda existir dentro de un conjunto de cosas.

P: ¿Cuáles son los dos conjuntos asociados a las funciones?

R: El conjunto de todos los valores que puede tener x se llama dominio y el conjunto que contiene todos los valores que puede tener y se llama codominio.

P: ¿Cómo se suelen denotar las funciones?

R: Las funciones se suelen denotar con letras cursivas como f, g, h.

P: ¿Cómo representamos una función?

R: Representamos una función escribiendo y = f(x), donde f es el nombre de la función y se escribe f : X → Y (función de X a Y) para representar las tres partes de la función - dominio (X), codominio (Y) y proceso de emparejamiento (la flecha).

P: ¿Puede dar un ejemplo de función?

R: Un ejemplo de función es f(x) = x + 1. Uno da un número natural x como entrada y obtiene un número natural y que es x + 1. Por ejemplo, al dar 3 como entrada a f se obtiene como salida 4.

P: ¿Todas las funciones tienen que ser una ecuación?

R: No, no todas las funciones necesitan ser una ecuación. La idea principal de las funciones es que las entradas y las salidas se emparejen de alguna manera, aunque pueda ser muy complicado.