Vector | objeto matemático

Ejemplos de vectores

• Juan camina 20 metros hacia el norte. La dirección "norte" junto con la distancia "20 metros" es un vector.
• Una manzana cae hacia abajo a 10 metros por segundo. La dirección "hacia abajo" combinada con la velocidad "10 metros por segundo" es un vector. Este tipo de vector también se llama velocidad.

 

Ejemplos de escalares

• La distancia entre dos lugares es de 10 kilómetros. Esta distancia no es un vector porque no contiene una dirección.
• El número de frutas en una caja no es un vector.
• Una persona que señala no es un vector porque sólo hay una dirección. No hay magnitud (la distancia del dedo de la persona a un edificio, por ejemplo).
• La longitud de un objeto.
• Un coche circula a 100 kilómetros por hora. Esto no describe un vector, ya que sólo hay una magnitud, pero no una dirección.

 

Más ejemplos de vectores

• El desplazamiento es un vector. El desplazamiento es la distancia que recorre algo en una dirección determinada. Una medida de distancia sola es un escalar.
• La fuerza que incluye la dirección es un vector.
• La velocidad es un vector, porque es una velocidad en una dirección determinada.
• La aceleración es el índice de cambio de velocidad. Un objeto se acelera si cambia de velocidad o de dirección.

 

Cómo añadir vectores

Añadir vectores en el papel utilizando el método de la cabeza a la cola

El método de suma de vectores de cabeza a cola es útil para hacer una estimación sobre el papel del resultado de la suma de dos vectores. Para ello

• Cada vector se dibuja como una flecha con una cantidad de longitud detrás, donde cada unidad de longitud en el papel representa una determinada magnitud del vector.
• Dibuje el siguiente vector, con la cola(extremo) del segundo vector en la cabeza(frente) del primer vector.
• Repita la operación para todos los vectores posteriores: Dibuje la cola del siguiente vector en la cabeza del anterior.
• Dibuje una línea desde la cola del primer vector hasta la cabeza del último vector - esa es la resultante(suma) de todos los vectores.

Se llama método "Head to Tail", porque cada cabeza del vector anterior lleva a la cola del siguiente.

Uso de la forma de los componentes

^{[necesita ser explicado ]}

Utilizar la forma de componentes para sumar dos vectores significa literalmente sumar las componentes de los vectores para crear un nuevo vector. Por ejemplo, sean a y b dos vectores bidimensionales. Estos vectores pueden escribirse en términos de sus componentes.

a = ( a x , a y ) {\displaystyle \mathbf {a} =(a_{x},a_{y})}

b = ( b x , b y ) {\displaystyle \mathbf {b} =(b_{x},b_{y})}

Supongamos que c es la suma de estos dos vectores, de modo que c = a + b. Esto significa que c = ( a x + b x , a y + b y ) {\displaystyle \mathbf {c} =(a_{x}+b_{x},a_{y}+b_{y})} .

He aquí un ejemplo de suma de dos vectores, utilizando sus formas componentes:

a = ( 3 , - 1 ) {\displaystyle \mathbf {a} =(3,-1)}

b = ( 2 , 2 ) {\mathbf =(2,2)}

c = a + b = ( a x + b x , a y + b y ) = ( 3 + 2 , - 1 + 2 ) = ( 5 , 1 ) {\displaystyle {\begin{aligned}\mathbf {c} &=\mathbf {a} +\mathbf {b} \\&=(a_{x}+b_{x},a_{y}+b_{y})\\&=(3+2,-1+2)\\&=(5,1)\end{aligned}}}

Este método funciona para todos los vectores, no sólo los bidimensionales.

 
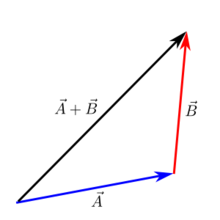
Adición de cabeza a cola  

Cómo multiplicar vectores

Utilizando el producto punto

El producto punto es un método para multiplicar vectores. Produce un escalar. Utiliza la forma de los componentes:

a = ( 2 , 3 ) b = ( 1 , 4 ) a ⋅ b = ( 2 , 3 ) ⋅ ( 1 , 4 ) = ( 2 ⋅ 1 ) + ( 3 ⋅ 4 ) = 2 + 12 = 14 {\displaystyle {\begin{aligned}\mathbf {a} &=(2,3)\Nmathbf {b} &=(1,4)\Nmathbf {a} \Ny =(2,3)\Nmathbf (1,4)\Ny =(2\cdot 1)+(3\cdot 4)\Ny =2+12\Ny =14\Nfinal{alineado}}.

Utilizando el producto cruzado

El producto cruzado es otro método para multiplicar vectores. A diferencia del producto punto, produce un vector. Utilizando la forma de los componentes:

a × b = | a | | b | sin ( θ ) n {\displaystyle \mathbf {a} |mathbf {b} =|mathbf {a} |||mathbf {b} |sin(\theta )|mathbf {n} }

Aquí, | a | {\displaystyle |mathbf {a} |} significa la longitud de un {\displaystyle \mathbf {a} } , y n {\displaystyle \mathbf {n} } es el vector unitario en ángulo recto tanto de a {\displaystyle \mathbf {a} } y b {\displaystyle \mathbf {b} } .

Multiplicar por un escalar

Para multiplicar un vector por un escalar (un número normal), se multiplica el número por cada componente del vector:

c x = ( c x 1 , c x 2 , . . . , c x n ) {\displaystyle c\,\mathbf {x} =(c\,x_{1},c\_{2},...,c\_{n})}

Un ejemplo de ello es

c = 5 x = ( 3 , 4 ) c x = ( 5 ⋅ 3 , 5 ⋅ 4 ) = ( 15 , 20 ) {\displaystyle {\begin{aligned}c&=5\mathbf {x} &=(3,4)\\c,\mathbf {x} &=(5\cdot 3,5\cdot 4)\c&=(15,20)\cend{aligned}}.

 

Páginas relacionadas

• Geometría analítica
• Vector nulo
• Vector de la unidad
• Campo vectorial
• Gráficos vectoriales
• Espacio vectorial
• Subespacio vectorial