Producto cruzado (producto vectorial): definición, propiedades y cálculo

Producto cruzado: definición, propiedades y cálculo paso a paso. Aprende a obtener el vector perpendicular en 3D con ejemplos y fórmulas claras.

Autor: Leandro Alegsa

23-03-2026 21:14

El producto cruzado es una operación matemática que puede realizarse entre dos vectores. Tras realizar el producto cruzado, se forma un nuevo vector. El producto cruzado de dos vectores es siempre perpendicular a los dos vectores "cruzados". Esto significa que el producto cruzado debe utilizarse siempre en un espacio tridimensional.

Definición y fórmula

Dados dos vectores en R³, a = (a1, a2, a3) y b = (b1, b2, b3), su producto cruzado a × b es el vector

a × b = (a2·b3 − a3·b2, a3·b1 − a1·b3, a1·b2 − a2·b1).

Otra forma habitual de calcularlo usa la notación determinantal con los vectores unitarios i, j, k:

a × b = det

i j k
a1 a2 a3
b1 b2 b3

Interpretación geométrica

Dirección: a × b es perpendicular a los planos que contienen a y b. La dirección se determina por la regla de la mano derecha: si los dedos van de a hacia b, el pulgar apunta en la dirección de a × b.
Sentido: el producto no es conmutativo: a × b = −(b × a).
Magnitud: |a × b| = |a|·|b|·sin(θ), donde θ es el ángulo entre a y b. Esto también representa el área del paralelogramo formado por a y b.

Propiedades importantes

Anticonmutatividad: a × b = − b × a.
Distributividad respecto a la suma: a × (b + c) = a × b + a × c.
Compatibilidad con escalares: (k a) × b = a × (k b) = k (a × b) para cualquier escalar k.
No es asociativo: (a × b) × c ≠ a × (b × c) en general.
Producto triple (escalares): a · (b × c) = det([a b c]) — el producto escalar de a con (b × c) da el volumen orientado del paralelepípedo formado por a, b y c. Es invariante por permutaciones cíclicas.
Identidad del producto triple vectorial: a × (b × c) = b (a·c) − c (a·b).
Caso degenerado: si a y b son paralelos (θ = 0 o π) o alguno es el vector cero, entonces a × b = 0.

Cálculo paso a paso: ejemplo numérico

Sea a = (1, 2, 3) y b = (4, 5, 6). Entonces

a × b = (a2·b3 − a3·b2, a3·b1 − a1·b3, a1·b2 − a2·b1)

Calculando componentes:

x = 2·6 − 3·5 = 12 − 15 = −3
y = 3·4 − 1·6 = 12 − 6 = 6
z = 1·5 − 2·4 = 5 − 8 = −3

Por tanto, a × b = (−3, 6, −3). Su magnitud es |a × b| = sqrt((−3)² + 6² + (−3)²) = sqrt(9 + 36 + 9) = sqrt(54) = 3·sqrt(6).

Aplicaciones y comentarios

Física: el torque τ aplicado a una partícula se define como τ = r × F, donde r es el vector posición y F la fuerza. La dirección del torque indica el eje de rotación.
Geometría: el módulo |a × b| da el área del paralelogramo formado por a y b; la semisuma (|a × b|/2) da el área del triángulo definido por a y b.
Generalizaciones: el producto cruzado, tal como se define, es específico de R³. En dimensiones superiores se utilizan objetos relacionados como el producto exterior (wedge product) que produce bivectores; existen productos análogos en dimensiones concretas (por ejemplo en R^7) pero con propiedades especiales y contexto avanzado.

Resumen rápido

El producto cruzado de dos vectores en R³ produce un vector perpendicular a ambos.
Magnitud: |a × b| = |a|·|b|·sin(θ).
Dirección determinada por la regla de la mano derecha.
Propiedades clave: anticonmutativo, distributivo, compatible con escalares; no asociativo.
Se usa para calcular áreas, momentos (torque) y volúmenes (producto triple).

Importancia del producto cruzado

Al tratarse de una operación vectorial, el producto cruzado es muy importante en todo tipo de ciencias (especialmente en física), ingeniería y matemáticas. Un ejemplo importante del producto cruzado es el par o el momento. Otra aplicación importante es el campo magnético.

Visualización del producto cruzado en tres dimensiones

El producto cruzado de a → {\displaystyle {\vec {a}} ${\vec {a}}$ y b → {\displaystyle {\vec {b}} ${\vec {b}}$ es un vector que llamaremos c → {\displaystyle {\vec {c}} ${\vec {c}}$ :

c → = a → × b → {\cvec {}}={vec {a}} {veces {b}} ${\vec {c}}={\vec {a}}\times {\vec {b}}$

Entonces, la magnitud de c → {\displaystyle {\vec {c}} ${\vec {c}}$ viene dada por:

c = | c → | = | a → | b → | sin θ = a b sin θ {\displaystyle c=|{vec {c}}|=|{vec {a}}||{vec {b}}|sin \theta =ab\sin \theta } $c=|{\vec {c}}|=|{\vec {a}}||{\vec {b}}|\sin \theta =ab\sin \theta$ ,

donde θ {\displaystyle \theta } $\theta$ es el ángulo entre a → {\displaystyle {\vec {a}} ${\vec {a}}$ y b → {\displaystyle {\vec {b}} ${\vec {b}}$ . El vector a → × b → {\displaystyle {\vec {a}}times {\vec {b}} ${\vec {a}}\times {\vec {b}}$ es perpendicular tanto a → {displaystyle {\vec {a}} ${\vec {a}}$ como a b → {\displaystyle {\vec {b}} ${\vec {b}}$ . La dirección de a → × b → {\displaystyle {\vec {a}}times {\vec {b}} ${\vec {a}}\times {\vec {b}}$ está determinada por una variación de la regla de la mano derecha. Si se sostiene la mano derecha como se muestra en la figura, el pulgar está en la dirección de c → {\displaystyle {\vec {c}} ${\vec {c}}$ , el dedo índice indica la dirección de a → {\displaystyle {\vec {a}} ${\vec {a}}$ y tu segundo dedo señala la dirección de b → {\displaystyle {\vec {b}} ${\vec {b}}$ . Si el ángulo entre tus dedos índice y segundo es mayor de 180°, es necesario poner la mano boca abajo.

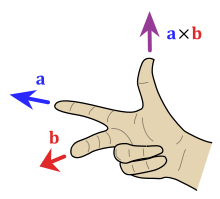
Encontrar la dirección del producto cruzado.

Cómo calcular el producto cruzado en notación vectorial

Como cualquier operación matemática, el producto cruzado puede realizarse de forma sencilla.

Dos dimensiones

Si
a → = ⟨ a 1 , a 2 ⟩ {\displaystyle {\vec {a}}=\lángulo a_{1},a_{2}} ${\vec {a}}=\langle a_{1},a_{2}\rangle$
y
b → = ⟨ b 1 , b 2 ⟩ {\displaystyle {\vec {b}}=\lángulo b_{1},b_{2}\rangle } ${\vec {b}}=\langle b_{1},b_{2}\rangle$
entonces
a → × b → = ( a 1 b 2 - a 2 b 1 ) k ^ {\displaystyle {\vec {a}\times {\vec {b}}=(a_{1}b_{2}-a_{2}b_{1}){\hat {k}}} ${\vec {a}}\times {\vec {b}}=(a_{1}b_{2}-a_{2}b_{1}){\hat {k}}$

o

a → × b → = c → {\a} {vec {a} {veces {b}}= {vec {c}} ${\vec {a}}\times {\vec {b}}={\vec {c}}$
y
c → = ⟨ 0 , 0 , a 1 b 2 - a 2 b 1 ⟩ = ( a 1 b 2 - a 2 b 1 ) k ^ {\displaystyle {{vec {c}}={lángulo 0,0,a_{1}b_{2}-a_{2}b_{1}}rangle =(a_{1}b_2}-a_{2}b_{1}){\hat {k}} ${\vec {c}}=\langle 0,0,a_{1}b_{2}-a_{2}b_{1}\rangle =(a_{1}b_{2}-a_{2}b_{1}){\hat {k}}$

k ^ {\displaystyle {\hat {k}} ${\hat {k}}$ es sólo un símbolo que dice que nuestro nuevo vector apunta hacia arriba (en la dirección z). Si "cruzas" dos vectores que están ambos en el plano x-y, el producto siempre será perpendicular a ambos vectores, y si ambos vectores están en el plano x-y, la única forma de que sea perpendicular a ambos es que esté en la dirección z. Si el valor de a 1 b 2 - a 2 b 1 {\displaystyle a_{1}b_{2}-a_{2}b_{1}} $a_{1}b_{2}-a_{2}b_{1}$ es positivo, entonces apunta fuera de la página; si su valor es negativo, entonces apunta dentro de la página.

Tres dimensiones

Si
a → = ⟨ a 1 , a 2 , a 3 ⟩ {\displaystyle {\vec {a}}=\lángulo a_{1},a_{2},a_{3}} ${\vec {a}}=\langle a_{1},a_{2},a_{3}\rangle$
y
b → = ⟨ b 1 , b 2 , b 3 ⟩ {\displaystyle {\vec {b}}=\lángulo b_{1},b_{2},b_{3}} ${\vec {b}}=\langle b_{1},b_{2},b_{3}\rangle$
entonces
a → × b → = ⟨ a 2 b 3 - a 3 b 2 , a 3 b 1 - a 1 b 3 , a 1 b 2 - a 2 b 1 ⟩ {desde el estilo {vec {a}}=langulo a_{2}b_{3}-a_{3}b_{2},a_{3}b_{1}-a_{1}b_{3},a_{1}b_{2}a_{2}b_{1}}rangle } ${\vec {a}}\times {\vec {b}}=\langle a_{2}b_{3}-a_{3}b_{2},a_{3}b_{1}-a_{1}b_{3},a_{1}b_{2}-a_{2}b_{1}\rangle$

Propiedades básicas del producto cruzado

a → × b → = - b → × a → {\displaystyle {\vec {a}}=-{\vec {b}}={\vec {a}}}. ${\vec {a}}\times {\vec {b}}=-{\vec {b}}\times {\vec {a}}$

a → × ( b → + c → ) = a → × b → + a → × c → {\vec {a} {veces ({\vec {b}+ {\vec {c}})= {\vec {a} {veces {b}+ {\vec {a} {veces {vec {c}}} ${\vec {a}}\times ({\vec {b}}+{\vec {c}})={\vec {a}}\times {\vec {b}}+{\vec {a}}\times {\vec {c}}$

c ( a → × b → ) = ( c a → ) × b → = a → × ( c b → ) {\displaystyle c({\vec {a}}\times {\vec {b}})=(c{\vec {a})\times {\vec {b}}={\vec {a}\times (c{\vec {b}})} $c({\vec {a}}\times {\vec {b}})=(c{\vec {a}})\times {\vec {b}}={\vec {a}}\times (c{\vec {b}})$

Preguntas y respuestas

P: ¿Qué es el producto cruzado?

R: El producto cruzado es una operación matemática que se puede realizar entre dos vectores tridimensionales.

P: ¿Cómo se suele representar el producto cruz?

R: El producto cruz se suele representar con el símbolo × o \times.

P: ¿Qué ocurre después de realizar el producto cruz?

R: Después de realizar el producto cruz, se forma un nuevo vector.

P: ¿Cuál es la relación entre el vector producto cruz y los vectores "cruzados"?

R: El producto cruz de dos vectores es siempre perpendicular (forma un ángulo) a los dos vectores "cruzados".

P: ¿En qué dimensión funciona normalmente el producto cruzado?

R: Normalmente, el producto cruzado sólo funciona en el espacio tridimensional.

P: ¿Cuáles son las tres dimensiones en las que se puede realizar el producto cruzado?

R: Las tres dimensiones en las que se puede realizar el producto cruzado son arriba o abajo, izquierda o derecha y adelante o atrás.

P: ¿Por qué el producto cruzado normalmente sólo funciona en el espacio tridimensional?

R: Normalmente, el producto cruzado sólo funciona en el espacio tridimensional porque son las dimensiones en las que se puede ir hacia arriba o hacia abajo, hacia la izquierda o hacia la derecha, y hacia delante o hacia atrás.

Buscar dentro de la enciclopedia