Regla de la mano derecha: definición y uso en el producto cruzado
Aprende la regla de la mano derecha para determinar la dirección del producto cruzado: explicación paso a paso, ejemplos visuales y trucos prácticos para vectores en 3D.
La regla de la mano derecha es una convención en las matemáticas vectoriales y en física que permite determinar la dirección del producto cruzado entre dos vectores. El producto cruzado de dos vectores en el espacio tridimensional produce un tercer vector perpendicular a ambos, y la regla de la mano derecha indica hacia qué lado apunta ese vector resultante.
- Comienza con la mano derecha relajada y estira el índice hacia delante en la dirección del primer vector.
- Coloca el pulgar apuntando en la dirección del segundo vector, como si hicieras la señal de una pistola (pulgar y índice formando un plano).
- Gira la mano para que el medio quede perpendicular al plano formado por índice y pulgar; el dedo corazón señalará la dirección del producto cruzado. Asegúrate de que los tres dedos formen un ángulo recto entre sí.
De forma práctica: apunta el índice en la dirección del primer vector (a), apunta el pulgar en la dirección del segundo vector (b) y el dedo medio indicará la dirección de a × b. Si inviertes el orden de los factores (b × a), el vector resultante apunta en sentido contrario. Por eso es importante respetar el orden, tal como se indica en la expresión:
t h u m b → × p o i n t e r → = m i d l e → t h u m b → × p o i n t e r → = m i d l e → {\displaystyle {\vec {thumb}}\times {\vec {pointer}}= {\vec {middle}}
Propiedades relevantes del producto cruzado
- Perpendicularidad: a × b es perpendicular tanto a a como a b.
- Magnitud: |a × b| = |a| |b| sin(θ), donde θ es el ángulo (0 ≤ θ ≤ π) entre a y b. Es máxima cuando los vectores son perpendiculares y nula cuando son paralelos o antiparalelos.
- Anticonmutatividad: a × b = −(b × a).
- Linealidad: (αa + βc) × b = α(a × b) + β(c × b), para escalares α, β.
- Producto con sí mismo: a × a = 0 (vector nulo).
Representación en coordenadas
En coordenadas cartesianas si a = (a1, a2, a3) y b = (b1, b2, b3), entonces
a × b = (a2 b3 − a3 b2, a3 b1 − a1 b3, a1 b2 − a2 b1).
También puede verse como el determinante de una matriz con los vectores unitarios i, j, k en la primera fila.
Ejemplos y aplicaciones
- Física — Torque: el torque τ sobre un punto se calcula como τ = r × F (brazo de palanca r y fuerza F); su dirección indica el eje y sentido de la rotación según la regla de la mano derecha.
- Fuerza magnética (Ley de Lorentz): la fuerza sobre una carga en movimiento es F = q v × B; la dirección de F se determina con la regla de la mano derecha (para cargas positivas).
- Área y normal de una superficie: el producto cruzado de dos lados adyacentes de un paralelogramo da un vector cuya magnitud es el área del paralelogramo y cuya dirección es la normal al plano.
- Base canónica: i × j = k, j × k = i, k × i = j y las permutaciones inversas dan el negativo.
Consejos prácticos
- Usa siempre la mano derecha; la mano izquierda daría la dirección opuesta (regla de la mano izquierda se usa a veces para portadores de carga negativa en física).
- Si los vectores están en el plano de tu mesa, coloca el índice en la dirección del primero y gira la muñeca hasta alinear el pulgar con el segundo; el dedo medio señalará la dirección del producto.
- Para evitar errores, comprueba la magnitud con |a||b|sin(θ) y la perpendicularidad proyectando sobre componentes conocidas (i, j, k).
Con estos pasos y propiedades podrás aplicar la regla de la mano derecha de forma segura al calcular productos cruzados en problemas geométricos y físicos.

La orientación para zurdos se muestra a la izquierda, y la de diestros a la derecha.
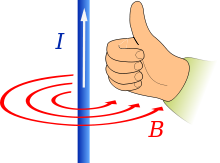
Predicción de la dirección del campo (B) cuando la corriente I fluye en la dirección del pulgar

La regla de la mano derecha para el movimiento producido con roscas de tornillo
Variaciones
Hay otra regla llamada regla de la mano derecha (o regla del sacacorchos) que se utiliza para los campos magnéticos y las cosas que giran.
1. Comienza poniendo la mano derecha en posición horizontal y apunta con el pulgar hacia fuera de forma que forme un ángulo recto con los demás dedos.
2. Ahora cierra los dedos en un puño y mantén el pulgar fuera (como un Thumbs Up).
3. Haz coincidir la forma en que se curvan tus dedos con la forma en que se mueve algo. La dirección a la que apunta tu pulgar es la dirección del vector que utilizamos para hablar de ello.
Puedes hacer esto a la inversa, iniciando el pulgar en la dirección del vector y ver cómo se curvan tus dedos para ver el sentido de la rotación. Si apuntas con el pulgar en la dirección de la corriente en un cable, el campo magnético que surge a su alrededor está en la dirección de tus dedos curvados.
Preguntas y respuestas
P: ¿Qué es la regla de la mano derecha?
R: La regla de la mano derecha es una convención en matemáticas vectoriales que le ayuda a recordar la dirección cuando los vectores se multiplican en cruz.
P: ¿Cómo se utiliza la regla de la mano derecha para averiguar la dirección de un producto cruzado?
R: Para averiguar la dirección de un producto cruzado, cierre la mano derecha y saque el dedo índice. Pegue el pulgar hacia arriba como si estuviera haciendo el signo de una pistola. Apunte con la "pistola" hacia delante, luego saque el dedo corazón de forma que apunte hacia la izquierda y todos los dedos formen un ángulo recto entre sí. Apunte con el pulgar en la dirección del primer vector y con el puntero en la dirección del segundo vector. Su dedo corazón apuntará en la dirección del producto cruzado.
P: ¿Qué ocurre si cambia el orden cuando los vectores se multiplican en cruz?
R: Si cambia el orden cuando los vectores se multiplican en cruz, el resultado irá en direcciones opuestas. Por lo tanto, es importante asegurarse de ir en el orden de pulgar x puntero = medio .
P: ¿Qué significa esta ecuación? {\displaystyle {\vec {pulgar}}veces {\vec {puntero}}={\vec {medio}} .
R: Esta ecuación significa que si se multiplican dos vectores cruzados entre sí (pulgar x puntero), se obtendrá un tercer vector (medio).
Buscar dentro de la enciclopedia