Producto escalar

Definición

El producto punto de dos vectores a = [a ₁, a ₂, ..., a _n] y b = [b ₁, b ₂, ..., b _n] se define como:

a ⋅ b = ∑ i = 1 n a i b i = a 1 b 1 + a 2 b 2 + ⋯ + a n b n {\displaystyle \cdot \mathbf {a} = suma _{i=1}^{n}a_{i}b_{i}=a_{1}b_{1}+a_{2}b_{2}+\cdots +a_{n}b_{n}.

donde Σ denota la notación de suma ( la suma de todos los términos) y n es la dimensión del espacio vectorial.

En dimensión 2, el producto punto de los vectores [a,b] y [c,d] es ac + bd. Del mismo modo, en una dimensión 3, el producto punto de los vectores [a,b,c] y [d,e,f] es ad + be + cf. Por ejemplo, el producto punto de dos vectores tridimensionales [1, 3, -5] y [4, -2, -1] es

[ 1 , 3 , - 5 ] ⋅ [ 4 , - 2 , - 1 ] = ( 1 × 4 ) + ( 3 × ( - 2 ) ) + ( ( - 5 ) × ( - 1 ) ) = ( 4 ) - ( 6 ) + ( 5 ) = 3. {\displaystyle [1,3,-5]\cdot [4,-2,-1]=(1\cdot 4)+(3\cdot (-2))+((-5)\cdot (-1))=(4)-(6)+(5)=3.}

Interpretación geométrica

En la geometría euclidiana, el producto punto, la longitud y el ángulo están relacionados. Para un vector a, el producto punto a - a es el cuadrado de la longitud de a, o

a ⋅ a = ‖ a ‖ 2 {\displaystyle {\mathbf {a} \cdot \mathbf {a} }=\mathbf {a} izquierda {=left||mathbf {a} \right|^{2}}

donde ||a|| denota la longitud (magnitud) de a. Más generalmente, si b es otro vector

a ⋅ b = ‖ a ‖ ‖ b ‖ cos θ {\cdot \mathbf {a} =\cdot \mathbf {b} =\cdot |mathbf {a} \right\\\\\\\\c, \cdot |mathbf {b} \...derecha... Cosas... Tetas...}

donde ||a|| y |b|| denotan la longitud de a y b y θ es el ángulo entre ellos.

Esta fórmula puede reordenarse para determinar el tamaño del ángulo entre dos vectores distintos de cero:

θ = arccos ( a ⋅ b ‖ a ‖ ‖ b ‖ ) {\displaystyle \theta =\arccos \left({\frac {{mathbf {a}}\cdot {\mathbf {b}}{left\||{mathbf {a}\right\||\left\|{mathbf {b}\right\})}

También se pueden convertir primero los vectores en vectores unitarios dividiendo por su magnitud:

a ^ = a ‖ a ‖ {\displaystyle {\boldsymbol {\hat {a}}={frac {\mathbf {a}}{left\||\mathbf {a}\right|}}

entonces el ángulo θ viene dado por

θ = arccos ( a ^ ⋅ b ^ ) {\displaystyle \theta =\arccos({\boldsymbol {\hat {a}}}\cdot {\boldsymbol {\hat {b}})}

Como el coseno de 90° es cero, el producto punto de dos vectores ortogonales (perpendiculares) es siempre cero. Además, dos vectores pueden considerarse ortogonales si y sólo si su producto puntual es cero, y ambos tienen una longitud distinta de cero. Esta propiedad proporciona un método sencillo para comprobar la condición de ortogonalidad.

A veces estas propiedades también se utilizan para definir el producto punto, especialmente en 2 y 3 dimensiones; esta definición es equivalente a la anterior. Para dimensiones superiores, la fórmula puede utilizarse para definir el concepto de ángulo.

Las propiedades geométricas se basan en que la base sea ortonormal, es decir, que esté compuesta por vectores perpendiculares entre sí con longitud unitaria.

Proyección escalar

Si tanto a como b tienen longitud uno (es decir, son vectores unitarios), su producto punto da simplemente el coseno del ángulo entre ellos.

Si sólo b es un vector unitario, entonces el producto punto a - b da |a| cos(θ), es decir, la magnitud de la proyección de a en la dirección de b, con un signo menos si la dirección es opuesta. Esto se denomina proyección escalar de a sobre b, o componente escalar de a en la dirección de b (ver figura). Esta propiedad del producto escalar tiene varias aplicaciones útiles (por ejemplo, véase la siguiente sección).

Si ni a ni b son vectores unitarios, entonces la magnitud de la proyección de a en la dirección de b, por ejemplo, sería a - (b / |b|) ya que el vector unitario en la dirección de b es b / |b|.

Rotación

Una rotación de la base ortonormal en términos de la cual se representa el vector a se obtiene con una multiplicación de a por una matriz de rotación R. Esta multiplicación matricial no es más que una representación compacta de una secuencia de productos punto.

Por ejemplo, dejemos que

• B ₁= {x, y, z} y B₂ = {u, v, w} sean dos bases ortonormales diferentes del mismo espacio R ³, con B ₂obtenida simplemente rotando B ₁,
• a ₁= (a_x , a_y , a_z ) representan el vector a en términos de B ₁,
• a ₂= (a_u , a_v , a_w ) representan el mismo vector en términos de la base rotada B ₂,
• u ₁, v ₁, w₁ son los vectores base rotados u, v, w representados en términos de B ₁.

A continuación, la rotación de B ₁a B₂ se realiza de la siguiente manera:

a 2 = R a 1 = [ u x u y u z v x v y v z w x w y w z ] [ a x a y a z ] = [ u 1 ⋅ a 1 v 1 ⋅ a 1 w 1 ⋅ a 1 ] = [ a u a v a w ] . {\displaystyle {\mathbf {a}}_{2}={\mathbf {Ra}}_{1}={\begin{bmatrix}u_{x}&u_{y}&u_{z}\\v_{x}&v_{y}&v_{z}\\w_{x}&w_{y}&w_{z}\end{bmatrix}}{\begin{bmatrix}a_{x}\\a_{y}\\a_{z}\end{bmatrix}}={\begin{bmatrix}{\mathbf {u}}_{1}\cdot {\mathbf {a}}_{1}\\{\mathbf {v}_1} {cdot}{mathbf}{1}{mathbf}{w}{1}{cdot}{mathbf}{1}{final}={begin{bmatrix}{a}{u}{v}{a}{w}{final}{bmatrix}. }

Obsérvese que la matriz de rotación R se ensambla utilizando los vectores base rotados u₁ , v ₁, w ₁como sus filas, y estos vectores son vectores unitarios. Por definición, Ra₁ consiste en una secuencia de productos escalares entre cada una de las tres filas de R y el vector a₁. Cada uno de estos productos escalares determina una componente escalar de a en la dirección de un vector base rotado (véase la sección anterior).

Si a₁ es un vector fila, en lugar de un vector columna, entonces R debe contener los vectores base rotados en sus columnas, y debe postmultiplicar a ₁:

a 2 = a 1 R = [ a x a y a z ] [ u x v x w x u y v y w y u z v z w z ] = [ u 1 ⋅ a 1 v 1 ⋅ a 1 w 1 ⋅ a 1 ] = [ a u a v a w ] . {\displaystyle {\mathbf {a}_{2}={mathbf {a}_{1}{mathbf {R}}={begin{bmatrix}a_{x}&a_{y}&a_{z}\end{bmatrix}}{\begin{bmatrix}u_{x}&v_{x}&w_{x}\\u_{y}&v_{y}&w_{y}\\u_{z}&v_{z}&w_{z}{final}={comenzar{bmatriz}{mathbf}{1}{cdot}{mathbf}{a}{1}{mathbf}{v}{1}{cdot}{mathbf}{a}{1}{cdot}{\mathbf {w}}_{1}\cdot {\mathbf {a}}_{1}\end{bmatrix}}={\begin{bmatrix}a_{u}&a_{v}&a_{w}\end{bmatrix}}. }

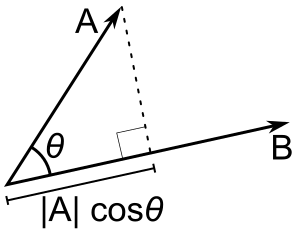
A - B = |A| |B| cos(θ). |A| cos(θ) es la proyección escalar de A sobre B.

Física

En física, la magnitud es un escalar en el sentido físico, es decir, una cantidad física independiente del sistema de coordenadas, expresada como el producto de un valor numérico y una unidad física, no sólo un número. El producto punto es también un escalar en este sentido, dado por la fórmula, independiente del sistema de coordenadas. Ejemplo:

• El trabajo mecánico es el producto punto de los vectores fuerza y desplazamiento.
• El flujo magnético es el producto punto del campo magnético y los vectores de área.
• El caudal volumétrico es el producto punto de la velocidad del fluido y los vectores de área.

Propiedades

Las siguientes propiedades se cumplen si a, b y c son vectores reales y r es un escalar.

El producto punto es conmutativo:

a ⋅ b = b ⋅ a . {\cdot \mathbf {a} \cdot \mathbf {b} =\mathbf {b} . \. }

El producto punto es distributivo sobre la suma de vectores:

a ⋅ ( b + c ) = a ⋅ b + a ⋅ c . {\displaystyle \mathbf {a} \cdot (\mathbf {b} +\mathbf {c} )=\mathbf {a} \cdot \mathbf {b} +\cdot \mathbf {c} . +mathbf {a} \cdot \mathbf {c} . }

El producto punto es bilineal:

a ⋅ ( r b + c ) = r ( a ⋅ b ) + ( a ⋅ c ) . {\displaystyle \mathbf {a} \cdot (r\mathbf {b} +\mathbf {c} )=r(\mathbf {a} \cdot \mathbf {b} )+(\mathbf {a} \cdot \mathbf {c} ). }

Cuando se multiplica por un valor escalar, el producto punto satisface:

( c 1 a ) ⋅ ( c 2 b ) = ( c 1 c 2 ) ( a ⋅ b ) {\displaystyle (c_{1}\mathbf {a} )\cdot (c_{2}\mathbf {b} )=(c_{1}c_{2})(\mathbf {a} \cdot \mathbf {b} )}}

(estas dos últimas propiedades se derivan de las dos primeras).

Dos vectores a y b distintos de cero son perpendiculares si y sólo si a - b = 0.

A diferencia de la multiplicación de números ordinarios, donde si ab = ac, entonces b siempre es igual a c a menos que a sea cero, el producto punto no obedece la ley de cancelación:

Si a - b = a - c y a ≠ 0, entonces podemos escribir: a - (b - c) = 0 por la ley distributiva; el resultado anterior dice que esto sólo significa que a es perpendicular a (b - c), lo que sigue permitiendo que (b - c) ≠ 0, y por tanto b ≠ c.

Siempre que la base sea ortonormal, el producto punto es invariante bajo cambios isométricos de la base: rotaciones, reflexiones y combinaciones, manteniendo el origen fijo. La interpretación geométrica mencionada anteriormente se basa en esta propiedad. En otras palabras, para un espacio ortonormal con cualquier número de dimensiones, el producto punto es invariante bajo una transformación de coordenadas basada en una matriz ortogonal. Esto corresponde a las dos condiciones siguientes:

• La nueva base vuelve a ser ortonormal (es decir, es ortonormal expresada en la antigua).
• Los nuevos vectores de la base tienen la misma longitud que los antiguos (es decir, longitud unitaria en términos de la base antigua).

Si a y b son funciones, entonces la derivada de a - b es a' - b + a - b'

Expansión del triple producto

Se trata de una identidad muy útil (también conocida como fórmula de Lagrange) que implica los productos punto y cruz. Se escribe como

a × ( b × c ) = b ( a ⋅ c ) - c ( a ⋅ b ) {\mathbf {a} \times (\mathbf {b} \times \mathbf {c} )=\mathbf {b} (\mathbf {a} \cdot \mathbf {c} )-\mathbf {c} (\mathbf {a} \cdot \mathbf {c} )-\mathbf {c} (\mathbf {a} \cdot \mathbf {b} )}

que es más fácil de recordar como "BAC menos CAB", teniendo en cuenta que los vectores están punteados. Esta fórmula se utiliza habitualmente para simplificar los cálculos vectoriales en física.

Prueba de la interpretación geométrica

Consideremos el elemento de R ⁿ

v = v 1 e ^ 1 + v 2 e ^ 2 + . . . + v n e ^ n . {\displaystyle \mathbf {v} =v_{1}\mathbf {\hat {e}} 1+v_2+mathbf {hat {e}} ...+v_{n}mathbf {\hat {e}} _{n}.\,}

La aplicación repetida del teorema de Pitágoras da como resultado para su longitud |v|

| v 2 = v 1 2 + v 2 2 + . . . + v n 2 . {\displaystyle |mathbf {v}} |^{2}=v_{1}^{2}+v_{2}^{2}+...+v_{n}^{2}.\,}

Pero esto es lo mismo que

v ⋅ v = v 1 2 + v 2 2 + . . . + v n 2 , {\displaystyle \mathbf {v} \cdot \mathbf {v} =v_{1}^{2}+v_{2}^{2}+...+v_{n}^{2},\cdot,}

por lo que concluimos que tomando el producto punto de un vector v por sí mismo se obtiene la longitud del vector al cuadrado.

Lema 1

v ⋅ v = | v | 2 . {\displaystyle \mathbf {v} \cdot \mathbf {v} =|\mathbf {v} |^{2}.\,}

Consideremos ahora dos vectores a y b que se extienden desde el origen, separados por un ángulo θ. Un tercer vector c puede definirse como

c = d e f a - b . {\displaystyle \mathbf {c} \ {\stackrel {\mathrm {def}} {\}}Mathbf {a} -{\}}mathbf {b} .\}

creando un triángulo con lados a, b y c. Según la ley de los cosenos, tenemos

| c | 2 = | a | 2 + | b | 2 - 2 | a | b | cos θ . {\displaystyle |mathbf {c} |^{2}=||mathbf {a} |^{2}+|||mathbf {b} |^{2}-2|||mathbf {a} ||\...que el de la velocidad... |\\\\N - |theta .\\N - ||mathbf.\N - |mathbf.|}

Sustituyendo los productos punto por las longitudes al cuadrado según el lema 1, obtenemos

c ⋅ c = a ⋅ a + b ⋅ b - 2 | a | b | cos θ . {\displaystyle \mathbf {c} \cdot \mathbf {c} =\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2|\mathbf {a} |||mathbf {b} |\cos \theta .\\_ (1)

Pero como c ≡ a - b, también tenemos

c ⋅ c = ( a - b ) ⋅ ( a - b ) {\cdot \mathbf {c} \cdot \mathbf {c} =(\mathbf {a} -\mathbf {b} )\cdot (\mathbf {a} -\mathbf {b} )\cdot ,

que, según la ley distributiva, se expande a

c ⋅ c = a ⋅ a + b ⋅ b - 2 ( a ⋅ b ) . {\displaystyle \mathbf {c} \cdot \mathbf {c} =\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \(2)

Fusionando las dos ecuaciones c - c, (1) y (2), obtenemos

a ⋅ a + b ⋅ b - 2 ( a ⋅ b ) = a ⋅ a + b ⋅ b - 2 | a | b | cos θ . {\displaystyle \mathbf {a} \cdot \mathbf {a} +\mathbf {b} -2(a) + b) )= a) + b) + b) )= a) + b) \...y el número de personas que se han quedado sin hogar... |||mathbf {b} ||cos \theta .\_}

Restando a - a + b - b de ambos lados y dividiendo por -2 queda

a ⋅ b = | a | b | cos θ . {\displaystyle \mathbf {a} \cdot \mathbf {b} =|\mathbf {a} ||mathbf {b} =|mathbf {a} =|mathbf {b} =|mathbf {b} |cos \theta .\_}

Q.E.D.

Generalización

The inner product generalizes the dot product to abstract vector spaces and is usually denoted by ⟨ a , b ⟩ {\displaystyle \langle \mathbf {a} \,,\mathbf {b} \N - Rangulo} . Debido a la interpretación geométrica del producto punto, la norma ||a|| de un vector a en dicho espacio de producto interior se define como

‖ a ‖ = ⟨ a , a ⟩ {\displaystyle \|\mathbf {a} \|={\sqrt {\langle \mathbf {a} \,,\mathbf {a} \rangle }}}

tal que generaliza la longitud, y el ángulo θ entre dos vectores a y b por

cos θ = ⟨ a , b ⟩ ‖ a ‖ b ‖ . {\displaystyle \cos {\theta }={frac {\langle \mathbf {a} \,,\mathbf {b} |mathbf {a},,|mathbf {b} \|}}. }

En particular, dos vectores se consideran ortogonales si su producto interior es cero

⟨ a , b ⟩ = 0. {\a6}Estilo de la pantalla \a6}Ángulo \a6},,\a6}Ángulo =0. \N - Rangulo =0.}

En el caso de los vectores con entradas complejas, el uso de la definición dada del producto escalar daría lugar a propiedades geométricas muy diferentes. Por ejemplo, el producto punto de un vector consigo mismo puede ser un número complejo arbitrario, y puede ser cero sin que el vector sea el vector cero; esto, a su vez, tendría graves consecuencias para nociones como la longitud y el ángulo. Muchas propiedades geométricas pueden salvarse, a costa de renunciar a las propiedades simétricas y bilineales del producto escalar, definiendo alternativamente

a ⋅ b = ∑ a i b i ¯ {\displaystyle \mathbf {a} \cdot \mathbf {b} =\sum {a_{i}{overline {b_i}}}}}

donde b_i es el conjugado complejo de b_i . Entonces el producto escalar de cualquier vector consigo mismo es un número real no negativo, y es distinto de cero excepto para el vector cero. Sin embargo, este producto escalar no es lineal en b (sino lineal conjugado), y el producto escalar tampoco es simétrico, ya que

a ⋅ b = b ⋅ a ¯ {\cdot \mathbf {a} \cdot \mathbf {b} = {\cdot \mathbf {b} \cdot \mathbf {a}} }}} .

Este tipo de producto escalar es, sin embargo, bastante útil, y conduce a las nociones de forma hermitiana y de espacios de producto interno general.

El producto interior de Frobenius generaliza el producto punto a las matrices. Se define como la suma de los productos de las correspondientes componentes de dos matrices que tienen el mismo tamaño.

Generalización a los tensores

El producto punto entre un tensor de orden n y un tensor de orden m es un tensor de orden n+m-2. El producto punto se calcula multiplicando y sumando a través de un solo índice en ambos tensores. Si A {\displaystyle \mathbf {A} } y B {\displaystyle \mathbf {B} son dos tensores con representación de elementos A i j ... k ℓ ... {\displaystyle A_{{puntos}}^{k\ell \dots }} y B m n ... p ... i {\displaystyle B_{mn\dots }^{p\dots }i} los elementos del producto punto A ⋅ B {\displaystyle \mathbf {A} \cdot \mathbf {B} } están dados por

A i j ... k ℓ ... B m n ... p ... i = ∑ i = 1 n A i j ... k ℓ ... B m n ... p ... i {\displaystyle A_{ij\dots }^k\ell \dots }B_{mn\dots }^{p{dots }i}={suma _{i=1}^{n}A_{ij\dots }^k\ell \dots }B_{mn\dots }^{p{dots }i}

Esta definición se reduce naturalmente al producto punto vectorial estándar cuando se aplica a vectores, y a la multiplicación de matrices cuando se aplica a matrices.

Ocasionalmente, se utiliza un producto doble de puntos para representar la multiplicación y la suma de dos índices. El producto doble por puntos entre dos tensores de segundo orden es un escalar.

Páginas relacionadas

• Desigualdad de Cauchy-Schwarz
• Producto cruzado
• Multiplicación de matrices
• Física