Función lineal

En matemáticas básicas, una función lineal es una función cuya gráfica es una línea recta en 2 dimensiones (ver imágenes). Un ejemplo es: y=2x-1. En matemáticas superiores, una función lineal suele referirse a una cartografía lineal.

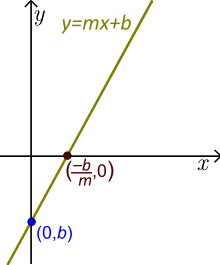
Función lineal (La línea aquí es genérica. Está inclinada por lo que m≠0. Vea los ejemplos con los valores reales de m y b más abajo).

Propiedades básicas

Formalmente, una función lineal es una función f(x):R→R tal que la gráfica de f es una recta. Esto significa que el dominio o entrada de f es un número real R y el rango o salida de f es también un número real R. Normalmente escribimos y(x) o simplemente y en lugar de f(x). Así que el enunciado formal significa:

introducimos o sustituimos un número real x en la función lineal
la función lineal produce o da un número real y y
todos estos puntos (x,y) forman una línea.

Hay tres formas principales de escribir las funciones lineales: pendiente-intercepto, estándar y paramétrica.

Forma de intersección de pendientes

La forma pendiente-intercepto (también llamada punto-pendiente o explícita) de una función lineal es y ( x ) = m x + b {\displaystyle y(x)=mx+b} $y(x)=mx+b$ o y = m x + b {\displaystyle y=mx+b} $y=mx+b$ . Esta forma tiene 2 variables x y у y 2 constantes m y b.

Las letras m y b son constantes. Antes de trabajar con una función lineal, sustituimos m y b por números reales reales.
Las letras x e y son variables.

La variable x se denomina variable independiente o argumento. Cualquier número real x puede introducirse o sustituirse en una función lineal. La función dará como resultado el valor correspondiente de y.
La variable y se denomina variable dependiente. Es el valor de salida después de sustituir un valor de entrada por x.

Se incluyen las líneas horizontales. La recta es horizontal si y sólo si m=0. Entonces tenemos simplemente y=b. Como b es un número real, se trata de una función constante. Así que una función constante es también una función lineal.
Las líneas verticales nunca se incluyen porque una línea vertical no es una función. Una línea vertical no pasa la prueba de la línea vertical. (Una recta vertical se define por la ecuación: x=b donde b es un número real).
Se incluyen las líneas inclinadas. La línea está inclinada si y sólo si m≠0.

La forma de intersección de la pendiente es única. Un valor diferente de m o un valor diferente de b da una línea diferente.
Una función lineal es una función polinómica de primer o nulo grado en una variable х .
El término constante es b. Si sustituimos x=0 en la función, obtenemos y=b. Así que el número b es la intersección y y la recta cruza el eje у en el punto (0,b).
Si m≠0, el número^–b /_m es la intersección o raíz x o cero y (^–b /_m ,0) es el punto donde la recta cruza el eje х. Aquí el valor de la función es cero.
El coeficiente m de x se llama pendiente o gradiente de la recta. Para cada recta, el número m es una constante, por lo que la pendiente es constante para toda la recta. La pendiente determina tanto la dirección como la inclinación de la recta. La dirección y la inclinación se denominan tasa de cambio. Así que la tasa de cambio es m y es constante para cada línea.

El signo de m determina la dirección. Si m>0, la función lineal es creciente; si m<0, la función es decreciente.
El valor absoluto de m determina la inclinación. Si |m|<1, la pendiente es suave; si |m|>1, la pendiente es pronunciada.
Si la pendiente de una recta es m y (х,у) es un punto cualquiera de la recta, debemos tener también el punto (х+1, y+m) en la recta.

Ejemplo: y=-2x+4. La pendiente es m= -2 y la intersección de y es b=4 o el punto (0,4). Sustituyendo y=0 y resolviendo para x, obtenemos 0=-2x+4 o x=2. Así que x=2 es la raíz de esta función lineal y el punto (2,0) es la intersección en x. Como la pendiente es m = -2, la recta es decreciente. Como |-2|=2>1, la disminución es relativamente pronunciada. Por cada cambio en х de 1 (hacia la derecha), el valor de у cambia -2 (baja).

La gráfica de una recta está determinada por dos puntos. Para graficar una función lineal, podemos sustituir dos valores diferentes de x en la función y resolver los valores correspondientes de y. Graficamos estos dos puntos. Con la ayuda de una regla, trazamos la recta que pasa por estos dos puntos y la prolongamos más allá de ambos.

Ejemplo: y=-2x+4. Sustituyendo x=0 obtenemos y=4 (es la intersección y) y por tanto el punto (0,4). Sustituyendo x=1, obtenemos y=2 y por tanto el punto (1,2). Traza estos puntos y dibuja la recta. (Observa que el segundo punto está a 1 a la derecha y 2 abajo del primer punto. Como dijimos en el ejemplo anterior, esto ocurre porque la pendiente es m= -2)

Una función lineal que no es una función constante es una biyección. Dará salida a cada número real (suryección) para exactamente un valor de entrada (inyección).

Ejemplo: y= -x+2. Supongamos que y= -1. Sustituimos y= -1 y obtenemos -1= -'x+2 o x=3. Esta es la única solución. Podemos hacer esto para cualquier valor de y.

Formulario estándar

A x + B y = C , B ≠ 0 {\displaystyle Ax+By=C,\neq 0} $Ax+By=C,\,B\neq 0$ .

La forma estándar tiene 2 variables x y у y 3 constantes A, B y C que se sustituyen por números reales reales antes de trabajar. Esta forma se utiliza a menudo en geometría y en sistemas de ecuaciones lineales.

Ejemplo: La función lineal 3x-2y=1 está en forma estándar. Las constantes son A=3, B=-2 y C=1.

Esta forma se escribe a veces como A x + B y + C = 0 {\displaystyle Ax+By+C=0} $Ax+By+C=0$ . Así, en lugar de escribir 3x-2y=1, escribimos la ecuación equivalente 3x-2y-1=0.
Las constantes A, B y C no están determinadas de forma única. Si las multiplicamos por un factor k, el valor de estas constantes cambia, pero la recta sigue siendo la misma.

Ejemplo: Las rectas 3x-2y=1 y 6x-4y=2 son coincidentes (misma recta). Aquí el factor es: k=2. Multiplicamos la primera ecuación por 2 para obtener la segunda ecuación. La forma única de intersección de la pendiente de esta recta es: y=1,5x-0,5 (resuelve cualquiera de las dos ecuaciones para y).

Forma vectorial-paramétrica

Forma paramétrica: { x ( t ) = x 1 + a 1 t y ( t ) = y 1 + a 2 t a 1 ≠ 0 , t ∈ R {{displaystyle \_left}} {{begin{array}{*{20}{l}{x_{1}+{a_{1}}t}{y(t)={y_{1}+{a_{2}}t}end{array}}}right. $\left\{{\begin{array}{*{20}{l}}{x(t)={x_{1}}+{a_{1}}t}\\{y(t)={y_{1}}+{a_{2}}t}\end{array}}\right.\,{a_{1}\neq 0}\,,\,t\in \mathbb {R}$

Forma vectorial: X = ( x 1 , y 1 ) + t ( a 1 , a 2 ) {\displaystyle {\mathbf {X} }=({x_{1},{y_{1})+t({a_{1},{a_{2})} ${\mathbf {X} }=({x_{1}},{y_{1}})+t({a_{1}},{a_{2}})$ o r ( t ) = < x 1 + a 1 t , y 1 + a 2 t > , a 1 ≠ 0 , t ∈ R {\displaystyle r(t)=,<x_{1}+a_{1}t,\,y_{1}+a_{2}t>,,\,{a_{1}neq 0},,\\\Nt en \mathbb {R} } $r(t)=\,<x_{1}+a_{1}t,\,y_{1}+a_{2}t>\,,\,{a_{1}\neq 0}\,,\,t\in \mathbb {R}$ .

La forma paramétrica o vectorial o vector-paramétrica tiene 1 parámetro t, 2 variables x y у, y 4 constantes a₁ , a₂ , x₁ , y₁ . Los coeficientes a₁ , a₂ , x₁ , y₁ no están determinados de forma única. La recta pasa por los puntos А=(x₁ ,y₁ ) y B=(x₁ +a₁ ,y₁ +a₂ ) por lo que si se toma cualquier otro punto o incluso se invierte el orden de los puntos se obtendrán diferentes constantes para la misma recta.
El parámetro t no es visible en el gráfico.
Los ingenieros suelen utilizar la letra t para el parámetro. Los matemáticos suelen utilizar la letra griega λ.

Ejemplo: X=(-1,1)+t(2,3), t∈R es una línea en forma de vector. Aquí: a₁ =2, a₂ =3, x₁ =-1 y x₂ =1. La recta pasa por los puntos (x₁ ,y₁ )=(-1,1) y (x₁ +a₁ ,y₁ +a₂ )=(1,4). La forma paramétrica correspondiente de esta recta es: x(t)= -1+2t, y(t)=1+3t. La forma única de intersección de pendientes de esta recta es: y(x)=1,5x+2,5 (resuelve la primera ecuación para t y sustituye este resultado en la segunda ecuación).

La forma vectorial-paramétrica de una línea se extiende naturalmente a las líneas en espacios de 3 dimensiones y superiores. Las otras formas no lo hacen.

Ejemplo: X=(-1,1,2)+t(2,3,-1), t∈R es una recta en un espacio tridimensional. La línea pasa por los puntos (-1,1,2) y (1,4,1).

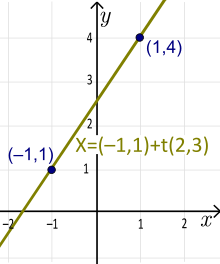
Forma vectorial-paramétrica de una recta (no única). La forma única pendiente-intercepto es y=1,5x+2,5

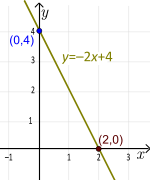
Forma de intersección de la pendiente de una línea (única)

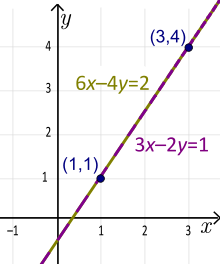
Forma estándar de una recta (no única). La forma única de intersección de pendientes es y=1,5x-0,5

Derivada de una función lineal

En el contexto en el que se define, la derivada de una función es una medida de la tasa de cambio de los valores de la función con respecto al cambio de los valores de entrada. Una función lineal tiene una tasa de cambio constante. Esta tasa de cambio es la pendiente m. Por tanto, m es la derivada. Esto se escribe a menudo:

( m x + b ) ′ = m {\displaystyle (mx+b)^{\prime }=m} $(mx+b)^{\prime }=m$

Ejemplo: y= -2x+4. Aquí m= -2 y por tanto y′= -2.

Función lineal vs. Ecuación lineal

A menudo se confunden los términos ecuación lineal y función lineal. Ambos son polinomios. Sin embargo, la palabra lineal en ecuación lineal significa que todos los términos con variables son de primer grado. (Una ecuación lineal puede tener 1, 2, 3 o más variables. Así que una ecuación lineal es una función lineal sólo si tiene exactamente 2 variables. (Una ecuación lineal en una variable es un punto en la recta numérica y una ecuación lineal en 3 variables es un plano en el espacio tridimensional).

Notación

Muchos países y disciplinas utilizan letras y ordenaciones diferentes para las distintas formas.

En muchos países, una función lineal se suele escribir como y = a x + b {\displaystyle y=ax+b} $y=ax+b$ donde a es la pendiente y b es la intersección y.

En los negocios y la economía, una función lineal se escribe a menudo como y = a + b x {\displaystyle y=a+bx} $y=a+bx$ donde a es la intersección y y b es la pendiente.

Páginas relacionadas

Línea
Polinomio
Función constante
Ecuación cuadrática
Ecuación lineal