Signo en matemáticas: definición, tipos (positivo y negativo) y símbolos

Descubre qué es el signo en matemáticas, tipos (positivo y negativo), su uso en números y símbolos como + y −. Explicaciones claras y ejemplos prácticos.

En matemáticas, el término signo suele referirse a la propiedad de un número real de ser positivo o negativo. Todo número real distinto de cero es positivo o negativo y, por tanto, se dice que tiene un signo. El propio cero no tiene signo (se considera neutro respecto al signo). Cuando un número aparece sin signo explícito se interpreta, por convención, como positivo.

Tipos de signo

• Signo positivo: indica que un número es mayor que cero. Se suele escribir con el símbolo + (aunque normalmente se omite el signo + en la notación diaria). Ejemplo: +5 o simplemente 5.
• Signo negativo: indica que un número es menor que cero y se representa con el símbolo −. Ejemplo: −3.

Símbolos y usos

• + (más): cumple dos funciones principales: como signo que indica positividad y como operador de suma o adición.
• − (menos): indica negatividad cuando se coloca delante de un número (signo unario) y actúa como resta cuando aparece entre dos operandos (operador binario).
• Otros signos matemáticos relacionados, como × o · (multiplicación), y ÷ o / (división), se usan en operaciones pero no representan “signo” en el sentido de positivo/negativo. La palabra signo también se emplea en contextos amplios para referirse a símbolos matemáticos, tal como ocurre con los signos de más y menos.

Reglas básicas con signos

• Producto de signos:
  • (+)(+) = +
  • (+)(−) = −
  • (−)(+) = −
  • (−)(−) = +
• Multiplicar por −1 cambia el signo de un número: −1·a = −a.
• La resta a − b equivale a sumar el opuesto: a − b = a + (−b).
• El valor absoluto |a| elimina el signo y devuelve la magnitud no negativa del número.

Función signo (signum)

En análisis se define la función signo, sgn(x), que indica el carácter signado de un número real:

• sgn(x) = 1 si x > 0
• sgn(x) = 0 si x = 0
• sgn(x) = −1 si x < 0

Esta función es útil para expresar fórmulas que dependen del signo de una variable, estudiar discontinuidades o definir operaciones que requieren conocer la orientación positiva/negativa de un valor.

Aplicaciones prácticas

• En álgebra, se usan tablas de signos para resolver desigualdades y estudiar el signo de polinomios o cocientes según intervalos entre raíces.
• En cálculo y análisis, el signo de una derivada indica crecimiento o decrecimiento de funciones.
• En física y otras ciencias, el signo indica dirección (por ejemplo, desplazamiento positivo/negativo) o sentido de cantidades vectoriales unidimensionales.

Observaciones y notas

• Los números complejos no están ordenados de forma compatible con los reales, por lo que no tienen un signo “positivo” o “negativo” en el sentido habitual.
• Es importante distinguir entre el signo unario (que transforma el número: −a) y el operador binario de resta (a − b).
• El concepto de “cambiar de signo” equivale a multiplicar por −1; hacerlo dos veces devuelve el valor original: −(−a) = a.

En resumen, el signo en matemáticas identifica si un número real es mayor o menor que cero, se representa sobre todo con los símbolos + y −, y tiene reglas claras en las operaciones algebraicas que permiten resolver desigualdades, operar con expresiones y analizar el comportamiento de funciones.

Significado de los signos

Como el cero no es ni positivo ni negativo, a veces se utiliza para referirse al signo de un número desconocido:

• Un número es positivo si es mayor que cero.
• Un número es negativo si es menor que cero.
• Un número es no negativo si es mayor o igual que cero.
• Un número es no positivo si es menor o igual a cero.

Así, un número no negativo es positivo o cero, mientras que un número no positivo es negativo o cero. Por ejemplo, el valor absoluto de un número real es siempre no negativo, pero no es necesariamente positivo.

La misma definición se utiliza a veces para las funciones que toman valores reales o enteros. Por ejemplo, una función se llamaría positiva si todos sus valores son positivos, o no negativa si todos sus valores son no negativos.

Signo de un ángulo

En muchos textos, es habitual ver un signo junto a la medida de un ángulo, en particular un ángulo localizado o un ángulo de rotación. En esta situación, el signo indica si el ángulo está en el sentido de las agujas del reloj o en sentido contrario. Aunque se pueden utilizar diferentes convenciones, es común en matemáticas que los ángulos en sentido contrario a las agujas del reloj cuenten como positivos, y los ángulos en sentido de las agujas del reloj cuenten como negativos.

También es posible poner un signo a un ángulo de rotación en tres dimensiones, suponiendo que el eje de rotación haya sido orientado. En concreto, un giro a la derecha alrededor de un eje suele contar como positivo, mientras que un giro a la izquierda cuenta como negativo.

Signo de una dirección

En aritmética y física, es habitual etiquetar ciertas direcciones como positivas o negativas. Como ejemplo básico, la recta numérica suele dibujarse con los números positivos a la derecha y los negativos a la izquierda:

En el plano cartesiano, las direcciones hacia la derecha y hacia arriba suelen considerarse positivas, siendo la dirección x positiva hacia la derecha y la dirección y positiva hacia arriba.

Otros significados

Además del signo de un número real, la palabra signo también se utiliza de varias formas relacionadas en las matemáticas y las ciencias:

• En la teoría de grafos, un grafo con signo es un grafo en el que cada arista se ha marcado con un signo positivo o negativo.
• En física, toda carga eléctrica tiene un signo, ya sea positivo o negativo. Según las reglas generales, una carga positiva es una carga con el mismo signo que la de un protón, y una carga negativa es una carga con el mismo signo que la de un electrón.

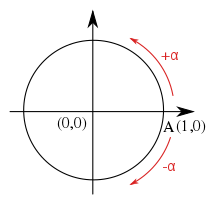
Midiendo desde el eje x, los ángulos en el círculo unitario cuentan como positivos en el sentido contrario a las agujas del reloj, y negativos en el sentido de las agujas del reloj.


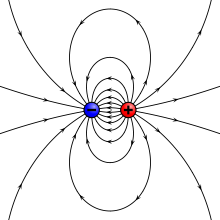
La carga eléctrica puede ser positiva o negativa.

Búsqueda por letra