Teoría de grafos: definición, conceptos y aplicaciones
Teoría de grafos: descubre definición, conceptos clave y aplicaciones prácticas para modelar relaciones y resolver problemas en redes, informática y ciencia de datos.
La teoría de grafos es un campo de las matemáticas que estudia los gráficos (habitualmente llamados grafos): una representación abstracta de un conjunto de puntos conectados por líneas. Cada punto suele llamarse vértice (plural: vértices) y las líneas se llaman aristas (o arcos en grafos dirigidos). Los grafos son una herramienta para modelar relaciones y estructuras y se utilizan para plantear y resolver una gran variedad de problemas en matemáticas, informática, ingeniería y otras disciplinas.
Algunas de las preguntas que plantea la teoría de grafos son:
- ¿Existe un camino entre dos vértices y cuál es el más corto?
- ¿Está el grafo conectado o dividido en componentes?
- ¿Tiene el grafo ciclos o es acíclico?
- ¿Se puede colorear el grafo con un número limitado de colores sin que dos vértices adyacentes compartan color?
- ¿Existe un camino que pase por todas las aristas una sola vez (recorrido euleriano) o por todos los vértices una sola vez (ciclo hamiltoniano)?
- ¿Cuál es el emparejamiento máximo entre conjuntos de vértices (problemas de matching)?
- ¿Cómo representar eficientemente el grafo y qué algoritmos permiten resolver problemas prácticos sobre él?
Conceptos básicos
- Vértice: nodo o elemento del grafo.
- Arista: conexión entre dos vértices; en grafos dirigidos las aristas tienen una dirección.
- Grado: número de aristas incidentes en un vértice (grado entrante y saliente en grafos dirigidos).
- Camino y ciclo: secuencias de vértices conectados por aristas; simple si no repite vértices.
- Componente conexa: subgrafo en el que cualquier par de vértices está conectado por un camino.
- Grafo dirigido vs no dirigido, grafo ponderado (con pesos en aristas), multigrafo (múltiples aristas entre dos vértices), grafo simple (sin lazos ni aristas múltiples).
- Árbol: grafo conectado y acíclico; bosque es una colección de árboles.
- Grafo bipartito, grafo completo (K_n), planar (puede dibujarse sin aristas que se crucen), etc.
Representaciones
- Matriz de adyacencia: matriz cuadrada donde la posición (i,j) indica si existe arista entre i y j. Útil para grafos densos y operaciones de álgebra lineal.
- Lista de adyacencia: para cada vértice, lista de vértices adyacentes. Más eficiente en memoria para grafos dispersos.
- Lista de aristas: colección de pares (o tuplas) que representan las aristas; útil para algoritmos que procesan aristas directamente.
Algoritmos fundamentales
- BFS (búsqueda en anchura) y DFS (búsqueda en profundidad): recorrer grafos, detectar componentes y ciclos.
- Dijkstra, Bellman–Ford y Floyd–Warshall: caminos más cortos (con y sin pesos negativos).
- Kruskal y Prim: árboles de expansión mínima.
- Ford–Fulkerson / Edmonds–Karp: cálculo de flujo máximo en redes.
- Algoritmos de matching (p. ej. Hopcroft–Karp para grafos bipartitos).
- Algoritmos para coloración, prueba de planaridad, y heurísticas para problemas NP-hard como el Traveling Salesman Problem o el problema del clique máximo.
Aplicaciones
- Redes de comunicación: modelado de Internet, enrutamiento y diseño de redes.
- Transporte y logística: planificación de rutas, rutas más cortas, asignación de recursos.
- Redes sociales: análisis de relaciones, centralidad, detección de comunidades.
- Química y biología: representación de moléculas, redes metabólicas y de interacción proteica.
- Optimización y operaciones: asignación, emparejamiento, flujo y corte mínimo.
- Ciencia de la computación: compiladores (dependencias), análisis de programas, bases de datos y algoritmos sobre grafos en bibliotecas y sistemas.
- Geografía y SIG: mapas, navegación y análisis espacial.
Propiedades teóricas y complejidad
Muchos problemas sobre grafos tienen soluciones eficientes (polinomiales), pero otros son intratables en la práctica porque son NP-completos o NP-hard (por ejemplo, el problema del coloring mínimo, el maximum clique o el traveling salesman en su forma general). La teoría de grafos combina resultados teóricos (criterios, teoremas y propiedades estructurales) con técnicas algorítmicas y heurísticas para abordar problemas reales.
Por qué es importante
La teoría de grafos proporciona un lenguaje y herramientas para modelar y analizar sistemas conectados. Su alcance interdisciplinario y su aplicabilidad a problemas prácticos la convierten en una pieza clave en investigación, ingeniería y tecnología. Aprender los conceptos básicos y los algoritmos fundamentales permite comprender y resolver situaciones complejas en muchos ámbitos.
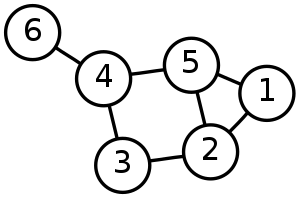
Un gráfico no dirigido.
Diferentes tipos de gráficos
- La teoría de los grafos tiene muchos aspectos. Los grafos pueden ser dirigidos o no dirigidos. Un ejemplo de grafo dirigido sería el sistema de carreteras de una ciudad. Algunas calles de la ciudad son de un solo sentido. Esto significa que en esas partes sólo se puede seguir una dirección.
- Los gráficos pueden ser ponderados. Un ejemplo sería una red de carreteras, con distancias, o con peajes (para carreteras).
- Los nodos (los círculos en el esquema) de un gráfico se llaman vértices. Las líneas que conectan los nodos se llaman aristas. Puede no haber ninguna línea entre dos nodos, puede haber una línea o puede haber múltiples líneas.
- En la teoría de grafos se utilizan mucho las estructuras de Árboles, que representan estructuras jerárquicas. Un Árbol es un grafo dirigido o no dirigido en el que no hay ningún ciclo, es decir: no hay forma de ir de un vértice (por ejemplo, una ciudad) al mismo utilizando cada arista que se usa una sola vez (caminar una sola vez por cada camino que se toma).
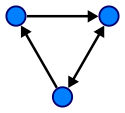
Un gráfico dirigido.
Historia
 →
→ →
→ 
Una visualización de los siete puentes de Königberg. Leonhard Euler resolvió este problema en 1736, lo que condujo al desarrollo de la topología, y a la teoría moderna de los grafos.
Un grafo es una estructura de datos abstracta. Contiene nodos que suelen estar relacionados entre sí. Un nodo es un conjunto de datos, normalmente en forma de pares ordenados. Los nodos están conectados o no conectados a otro nodo. La relación entre los nodos suele definirse como una arista. Los grafos son útiles por su capacidad de asociar nodos con otros nodos. En la práctica, existen algunas representaciones de los grafos.
Leonhard Euler vivía en una ciudad llamada Königsberg. (Su nombre cambió a Kaliningrado en 1946). La ciudad está en el río Pregel. Hay una isla en el río. Hay algunos puentes que cruzan el río. Euler quería pasear y utilizar cada uno de los puentes una vez. Preguntó si podía hacerlo. En 1736, publicó un artículo científico en el que demostraba que esto no era posible. Hoy en día, este problema se conoce como los Siete Puentes de Königsberg. El artículo se considera el primer documento de la historia de la teoría de los grafos.
Este artículo, al igual que el escrito por Vandermonde sobre el problema del caballero, continuó con el situs de análisis iniciado por Leibniz. La fórmula de Euler sobre el número de aristas, vértices y caras de un poliedro convexo fue estudiada y generalizada por Cauchy y L'Huillier, y está en el origen de la topología.
La fusión de las ideas procedentes de las matemáticas con las de la química está en el origen de una parte de la terminología estándar de la teoría de grafos. En concreto, el término "grafo" fue introducido por Sylvester en un artículo publicado en 1878 en Nature.
Uno de los problemas más famosos y productivos de la teoría de grafos es el problema de los cuatro colores: "¿Es cierto que cualquier mapa dibujado en el plano puede tener sus regiones coloreadas con cuatro colores, de forma que dos regiones cualesquiera que tengan un borde común tengan colores diferentes?"
.png)
El mismo problema, pero utilizando un gráfico
.png)
El problema del puente de Königsberg, en un mapa de la ciudad
La teoría de los grafos en perspectiva
La teoría de grafos es una parte importante de las matemáticas y la informática. Para muchos de estos problemas existen soluciones exactas. Sin embargo, muchas veces son muy difíciles de calcular. Por ello, muy a menudo se utilizan aproximaciones. Hay dos tipos de tales aproximaciones, los algoritmos de Monte-Carlo y los algoritmos de Las-Vegas.
Páginas relacionadas
Preguntas y respuestas
P: ¿Qué es la teoría de grafos?
R: La teoría de grafos es un campo de las matemáticas que estudia los grafos, que son representaciones abstractas de puntos conectados por líneas.
P: ¿Cómo se llaman los puntos de un gráfico?
R: Los puntos de un gráfico suelen denominarse vértices.
P: ¿Qué representan las líneas entre los vértices?
R: Las líneas entre los vértices representan relaciones o conexiones entre ellos.
P: ¿Cómo se pueden utilizar los gráficos?
R: Los gráficos pueden utilizarse para modelar relaciones y encontrar respuestas a diversos problemas.
P: ¿Qué tipo de preguntas pueden ayudar a responder los gráficos?
R: Los gráficos pueden ayudar a responder a preguntas relacionadas con el análisis de redes, la optimización y la programación.
P: ¿Existen diferentes tipos de gráficos?
R: Sí, hay diferentes tipos de grafos, como los dirigidos y los no dirigidos, los ponderados y los no ponderados, los completos y los incompletos, etc.
P: ¿Hay algún software disponible para trabajar con la teoría de grafos?
R: Sí, hay software disponible para trabajar con la teoría de grafos como Gephi y NetworkX.
Buscar dentro de la enciclopedia