Teorema de los cuatro colores: definición, historia y demostración
Explora el Teorema de los Cuatro Colores: definición, historia y demostración, incluida la prueba por ordenador que resolvió este clásico problema matemático.
El teorema de los cuatro colores es un teorema de las matemáticas que establece que cualquier división de una superficie plana en regiones (lo que popularmente se considera un mapa) puede colorearse con, como máximo, cuatro colores de modo que dos regiones adyacentes no compartan el mismo color. Bajo esta definición, dos regiones son adyacentes cuando comparten un segmento de borde (no basta con que se toquen en un punto).
Historia breve
El problema fue planteado por primera vez en 1852 por Francis Guthrie y se difundió en la comunidad matemática. A lo largo de más de un siglo aparecieron numerosas afirmaciones, demostraciones incompletas y contraejemplos erróneos.
- En 1879 Alfred Kempe publicó una demostración clásica que fue aceptada durante años; sin embargo, en 1890 P. J. Heawood encontró un fallo en la prueba de Kempe. Aunque la demostración de Kempe no era correcta para el caso de cuatro colores, la misma técnica sí permitía demostrar el teorema de los cinco colores (Heawood, 1890), es decir, que cinco colores siempre bastan. La demostración del teorema de los cinco colores es corta y elemental y suele enseñarse como ejemplo introductorio.
- El primer resultado definitivo aceptado para los cuatro colores fue alcanzado en 1976 por Kenneth Appel y Wolfgang Haken mediante una prueba asistida por ordenador. Su método combinó la técnica de despacho (discharging) con la verificación por ordenador de un conjunto finito de configuraciones reducibles e inevitables; la primera versión contenía 1.936 casos. Esta prueba suscitó debate porque buena parte del trabajo de comprobación lo realizó un programa informático.
- Posteriores refinamientos, en particular la demostración de Neil Robertson, Daniel Sanders, Paul Seymour y Robin Thomas publicada en los años 1990 (conjunto inevitable reducido a unas 633 configuraciones), simplificaron y hicieron más manejable la verificación computacional.
- Para aumentar la confianza en la prueba por ordenador, en la década de 2000 Georges Gonthier formalizó una prueba del teorema en el sistema de demostración asistida Coq, lo que supuso un hito en la verificación formal de teoremas matemáticos complejos.
Idea y métodos de la demostración
La demostración moderna del teorema se apoya en conceptos de teoría de grafos. Un mapa planar se puede asociar a un grafo planar (o, alternativamente, se trabaja con el grafo dual) y el problema de colorear regiones se traduce en el de colorear vértices de un grafo de modo que vértices adyacentes tengan colores distintos —esto es, determinar el número cromático del grafo.
Dos ideas claves usadas en las pruebas son:
- Configuraciones reducibles e inevitables: se busca un conjunto finito de configuraciones que sea inevitable (cualquier grafo planar grande debe contener alguna de ellas) y demostrar que cada configuración es reducible (si apareciera, permitiría reducir el problema a uno más pequeño). Si se logra esto, por inducción no puede haber contraejemplo mínimo al teorema.
- Método de despacho (discharging): técnica combinatoria para probar que ciertos conjuntos de configuraciones son inevitables; distribuye “carga” entre vértices y caras del grafo planar y demuestra que alguna configuración buscada debe aparecer.
En las pruebas históricas aparecieron también las llamadas cadenas de Kempe, una idea útil que, aunque no bastó para la demostración de Kempe, sí resultó esencial para la prueba elemental del teorema de los cinco colores.
¿Por qué los cartógrafos no se preocupan?
Aunque el origen del problema fue la coloración de mapas políticos de países, esa aplicación práctica resulta poco exigente: muchos mapas reales se colorean con tres colores o incluso dos, y los que requieren exactamente cuatro son relativamente raros. Según un trabajo histórico citado por Kenneth May (Wilson 2002, 2), “los mapas que utilizan sólo cuatro colores son raros, y los que lo hacen suelen requerir sólo tres. Los libros sobre cartografía y la historia de la elaboración de mapas no mencionan la cuatricromía”.
Ejemplos, consecuencias y resultados relacionados
- Existen mapas y grafos planares cuyo número cromático es 4; un ejemplo sencillo desde la teoría de grafos es el grafo completo K4 (cuatro vértices todos mutuamente adyacentes), que es planar y requiere cuatro colores. Esto muestra que el límite cuatro es óptimo: a veces hacen falta exactamente cuatro colores.
- El teorema de los cinco colores garantiza que con cinco colores siempre es posible colorear cualquier mapa planar, y su demostración es bastante elemental en comparación con la del caso de cuatro colores.
- La caracterización de grafos planares por Kuratowski y Wagner (prohibición de los menores K5 y K3,3) es una herramienta clave en teoría de grafos relacionada con problemas de planaridad y coloración.
La controversia sobre las pruebas asistidas por ordenador
La primera demostración de Appel y Haken fue polémica porque la verificación de miles de casos se apoyó en programas informáticos; muchos matemáticos consideraron problemático no poder revisar a mano la totalidad del caso. Con el tiempo, la mejora de las técnicas, la reducción del número de configuraciones y la formalización en asistentes de prueba (por ejemplo, Coq) han aumentado la aceptación y la confianza en estas demostraciones. Hoy en día la comunidad matemática acepta el teorema como probado, aunque la discusión sobre la naturaleza y la verificación de las pruebas asistidas por ordenador sigue siendo relevante.
En resumen, el teorema de los cuatro colores es un resultado central en combinatoria y teoría de grafos: sencillo de enunciar, históricamente intrincado y relevante por las técnicas desarrolladas en su estudio (cadenas de Kempe, método de despacho, pruebas asistidas por ordenador y formalización).
Ejemplo de un mapa de cuatro colores
Tres colores no son suficientes para colorear este mapa.
Formulación exacta del problema
Intuitivamente, el teorema de los cuatro colores puede enunciarse como "dada una separación cualquiera de un plano en regiones contiguas, llamada mapa, las regiones pueden colorearse utilizando como máximo cuatro colores de manera que ninguna región adyacente tenga el mismo color". Para poder resolver correctamente el problema, es necesario aclarar algunos aspectos: En primer lugar, hay que ignorar todos los puntos que pertenecen a tres o más países. En segundo lugar, los mapas extraños con regiones de área finita y perímetro infinito pueden requerir más de cuatro colores.
A efectos del teorema, cada "país" tiene que ser una región simplemente conectada, o contigua. En el mundo real, esto no es cierto: Alaska como parte de Estados Unidos, Najchiván como parte de Azerbaiyán y Kaliningrado como parte de Rusia no son contiguos. Dado que el territorio de un determinado país debe ser del mismo color, cuatro colores pueden no ser suficientes. Por ejemplo, considere un mapa simplificado, como el que se muestra a la izquierda: En este mapa, las dos regiones etiquetadas como A pertenecen al mismo país, y deben ser del mismo color. Este mapa requiere entonces cinco colores, ya que las dos regiones A son contiguas a otras cuatro regiones, cada una de las cuales es contigua a todas las demás. Si A tuviera sólo tres regiones, podrían necesitarse seis o más colores. De este modo, es posible hacer mapas que necesiten un número arbitrario de colores. Una construcción similar se aplica también si se utiliza un único color para todas las masas de agua, como es habitual en los mapas reales.
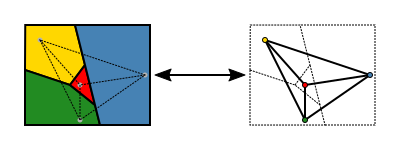
Una versión del teorema más fácil de enunciar utiliza la teoría de los grafos. El conjunto de regiones de un mapa puede representarse de forma más abstracta como un grafo no dirigido que tiene un vértice por cada región y una arista por cada par de regiones que comparten un segmento límite. Este grafo es plano: puede dibujarse en el plano sin cruces colocando cada vértice en una ubicación elegida arbitrariamente dentro de la región a la que corresponde, y dibujando las aristas como curvas que conducen sin cruces dentro de cada región desde la ubicación del vértice hasta cada punto límite compartido de la región. A la inversa, cualquier gráfico plano puede formarse a partir de un mapa de esta manera. En la terminología de la teoría de los grafos, el teorema de los cuatro colores afirma que los vértices de todo grafo planar pueden colorearse con un máximo de cuatro colores, de modo que no hay dos vértices adyacentes que tengan el mismo color, o para abreviar, "todo grafo planar es cuatricolorable" (Thomas 1998, p. 849; Wilson 2002).
Ejemplo de mapa de Azerbaiyán con regiones no contiguas
Este mapa no puede ser coloreado con cuatro colores
Historia
La primera persona que nombró el problema fue Francis Guthrie, en 1852. Por aquel entonces era un estudiante de derecho en Inglaterra. Descubrió que necesitaba al menos cuatro colores para colorear un mapa de los condados de Inglaterra. Augustus de Morgan discutió por primera vez el problema, en una carta que escribió a Rowan Hamliton en agosto de 1852. En la carta, de Morgan se pregunta si cuatro colores son realmente suficientes para colorear un mapa, de forma que los países que están uno al lado del otro reciban colores diferentes.
El matemático inglés Arthur Cayley presentó el problema a la sociedad matemática de Londres, en 1878. Al cabo de un año, Alfred Kempe encontró lo que parecía una prueba del problema. Once años después, en 1890, Percy Heawood demostró que la prueba de Alfred era errónea. Peter Guthrie Tait presentó otro intento de prueba en 1880. Se necesitaron once años para demostrar que la prueba de Tait tampoco funcionaba. En 1891, Julius Petersen pudo demostrarlo. Cuando falsificó la prueba de Cayley, Kempe también mostró una prueba para un problema que llamó Teorema de los cinco colores. El teorema dice que cualquier mapa de este tipo puede ser coloreado con no más de cinco colores. Hay dos restricciones: La primera es que cualquier país es contiguo, no hay exclaves. La segunda restricción es que los países deben tener una frontera común; si sólo se tocan en un punto, pueden ser coloreados con el mismo color. Aunque la prueba de Kempe era errónea, utilizó algunas de las ideas que más tarde permitirían una prueba correcta.
En los años 60 y 70, Heinrich Heesch desarrolló un primer esbozo de prueba por ordenador. Kenneth Appel y Wolfgang Haken mejoraron este esbozo en 1976 (Robertson et al. 1996). Consiguieron reducir el número de casos que había que probar a 1936; se hizo una versión posterior que se basaba en probar sólo 1476 casos. Cada caso debía ser probado por un ordenador (Appel & Haken 1977) harv error: objetivos múltiples (2×): CITEREFAppelHaken1977 (ayuda).
En 1996, Neil Robertson, Daniel Sanders, Paul Seymour y Robin Thomas mejoraron el método y redujeron el número de casos a probar a 663. De nuevo, cada caso debía ser probado por ordenador.
En 2005, Georges Gonthier y Benjamin Werner desarrollaron una prueba formal. Esto supuso una mejora, ya que permitió utilizar, por primera vez, un software de demostración de teoremas. El software utilizado se llama Coq.
El teorema de los cuatro colores es el primer gran problema matemático que se demostró con la ayuda de un ordenador. Como la demostración no puede ser realizada por un humano, algunos matemáticos no la reconocieron como correcta. Para verificar la prueba, es necesario contar con un software y un hardware que funcionen correctamente para validar la prueba. Como la prueba se hizo por ordenador, tampoco es muy elegante.
Intentos que resultaron erróneos
El teorema de los cuatro colores ha sido notorio por atraer un gran número de pruebas y refutaciones falsas en su larga historia. Al principio, The New York Times se negó a informar sobre la prueba de Appel-Haken. El periódico lo hizo por una cuestión de política; temía que la prueba se demostrara falsa como las anteriores (Wilson 2002, p. 209). Algunas pruebas tardaron mucho tiempo, hasta que pudieron ser falsificadas: En el caso de las pruebas de Kempe y Tait, falsificarlas llevó más de una década.
Los contraejemplos más sencillos suelen tratar de crear una región que toque a todas las demás. Esto obliga a colorear las regiones restantes con sólo tres colores. Como el teorema de los cuatro colores es cierto, esto siempre es posible; sin embargo, como la persona que dibuja el mapa está centrada en la única región grande, no se da cuenta de que las regiones restantes pueden, de hecho, colorearse con tres colores.
Este truco puede generalizarse: Si los colores de algunas regiones de un mapa se eligen de antemano, resulta imposible colorear las regiones restantes de forma que en total sólo se utilicen cuatro colores. Alguien que verifique el contraejemplo puede no pensar que puede ser necesario cambiar el color de estas regiones. Esto hará que el contraejemplo parezca válido, aunque no lo sea.
Tal vez un efecto que subyace a este error común es el hecho de que la restricción de color no es transitiva: una región sólo tiene que ser coloreada de forma diferente a las regiones que toca directamente, no a las regiones que tocan a las que toca. Si esta fuera la restricción, los grafos planares requerirían un número arbitrario de colores.
Otras falsas refutaciones violan los supuestos del teorema de formas inesperadas, como el uso de una región que tiene múltiples partes desconectadas, o no permitir que regiones del mismo color se toquen en un punto.
El mapa (izquierda) ha sido coloreado con cinco colores, y es necesario cambiar al menos cuatro de las diez regiones para obtener una coloración con sólo cuatro colores (derecha).
Colorear mapas políticos
En la vida real, muchos países tienen exclaves o colonias. Dado que pertenecen al país, es necesario colorearlos con el mismo color que el país matriz. Esto significa que, normalmente, se necesitan más de cuatro colores para colorear un mapa de este tipo. Cuando los matemáticos hablan del gráfico asociado al problema, dicen que no es plano. Aunque es fácil comprobar si un gráfico es planar, encontrar el menor número de colores necesarios para colorearlo es muy difícil. Es NP-completo, que es uno de los problemas más difíciles que existen. El menor número de colores necesarios para colorear un grafo se conoce como su número cromático. Muchos de los problemas que se plantean al intentar resolver el teorema de los cuatro colores están relacionados con las matemáticas discretas. Por esta razón, se suelen utilizar métodos de la topología algebraica.
Ampliación de los mapas "no planos
El teorema de los cuatro colores requiere que el "mapa" esté en una superficie plana, lo que los matemáticos llaman un plano. En 1890, Percy John Heawood creó lo que hoy se llama la conjetura de Heawood: Plantea la misma cuestión que el teorema de los cuatro colores, pero para cualquier objeto topológico. Como ejemplo, un toro puede ser coloreado con un máximo de siete colores. La conjetura de Heawood da una fórmula que funciona para todos esos objetos, excepto la botella de Klein.
Preguntas y respuestas
P: ¿Qué es el teorema de los cuatro colores?
R: El teorema de los cuatro colores es un teorema matemático que establece que en cualquier superficie plana con regiones, éstas no pueden ser coloreadas con más de cuatro colores. Las regiones adyacentes no deben tener el mismo color.
P: ¿Cómo se estableció la primera prueba del teorema de los cuatro colores?
R: La primera prueba del teorema de los cuatro colores fue una prueba por agotamiento con 1.936 casos. Esto significa que se estableció dividiéndolo en casos y probando cada uno por separado.
P: ¿Los cartógrafos están interesados en este problema?
R: No, los cartógrafos no están muy interesados en este problema ya que los mapas que utilizan sólo cuatro colores son raros y normalmente sólo requieren tres colores. Los libros sobre cartografía e historia de la elaboración de mapas no mencionan la propiedad de los cuatro colores.
P: ¿Qué es el teorema de los cinco colores?
R: El teorema de los cinco colores afirma que cinco colores son suficientes para colorear un mapa y tiene una prueba corta y elemental que se demostró a finales del siglo XIX.
P: ¿Qué dificultad entrañaba demostrar que sólo se necesitaban 4 colores para colorear los mapas?
R: Demostrar que sólo se necesitan 4 colores para colorear los mapas resultó ser mucho más difícil de lo esperado, ya que han aparecido muchas pruebas y contraejemplos falsos desde su primera afirmación en 1852.
P: ¿Existe algún ejemplo de mapa en el que sean necesarios 5 o más colores para colorear correctamente todas las regiones?
R: Sí, un ejemplo de este tipo es cuando una región está rodeada por un número impar de otras que se tocan entre sí en un ciclo - en este caso pueden ser necesarios 5 o más colores para colorear correctamente todas las regiones.
Buscar dentro de la enciclopedia