Conjunto | una idea de las matemáticas

Un conjunto es una idea de las matemáticas. Un conjunto tiene miembros (también llamados elementos). Un conjunto se define por sus miembros, por lo que dos conjuntos cualquiera con los mismos miembros son iguales (por ejemplo, si el conjunto X {\mathit {X}} ${\mathit {X}}$ y el conjunto Y {\mathit {Y}} ${\mathit {Y}}$ tienen los mismos miembros, entonces X = Y {\mathit {X}}={\mathit {Y}} ${\mathit {X}}={\mathit {Y}}$ ).

Un conjunto no puede tener el mismo miembro más de una vez. La pertenencia es lo único que importa. Por ejemplo, no hay ningún orden ni ninguna otra diferencia entre los miembros. Cualquier cosa puede ser miembro de un conjunto, incluidos los propios conjuntos (aunque si un conjunto es miembro de sí mismo, pueden darse paradojas como la de Russell).

Ejemplo de un conjunto de polígonos

La definición original de Cantor de un conjunto

Georg Cantor, en 1894. Cantor fue el primer matemático que habló de conjuntos

Qué hacer con los conjuntos

Imagine que el conjunto es una bolsa.

Elemento de

Se pueden meter varias cosas en una bolsa. Más adelante, una buena pregunta sería si una determinada cosa está en la bolsa. Los matemáticos llaman a esto elemento de. Algo es un elemento de un conjunto, si esa cosa puede encontrarse en la bolsa correspondiente. El símbolo que se utiliza para ello es ∈ {\displaystyle \in } $\in$ :

a ∈ A {\año a\año en {\año A}} $a\in {\mathit {A}}$ ,

lo que significa que un {\año} está en la bolsa A {\año}} ${\mathit {A}}$ o un {\año} es un elemento de A {\año}} ${\mathit {A}}$ .

A diferencia de una bolsa, un conjunto puede contener como máximo un elemento de un tipo determinado. Así, para un conjunto de frutas, daría igual si hay una naranja o si hay 10 naranjas.

Conjunto vacío

Al igual que una bolsa, un conjunto también puede estar vacío. El conjunto vacío es como una bolsa vacía: no tiene nada dentro. El "conjunto vacío" también se denomina conjunto nulo y se representa con el símbolo ∅ {\año} $\varnothing$ .

Universo

Si consideramos, digamos, algunos conjuntos de coches americanos, por ejemplo, un conjunto de todos los Ford y un conjunto de todos los Dodge, es posible que también queramos considerar el conjunto de los coches americanos. En este caso, el conjunto de todos los coches americanos se llamaría universo.

En otras palabras, un universo es una colección de todos los elementos que uno desea considerar en un problema dado. El universo se suele denominar U {designar U} $U$ .

Comparación de conjuntos

Se pueden comparar dos conjuntos. Esto es como mirar dentro de dos bolsas diferentes. Si contienen las mismas cosas, son iguales. No importa en qué orden estén estas cosas.

Por ejemplo, si A = { S t a n f o r d , S t a n l e y } {\displaystyle {\mathit {A}}={Stanford,Stanley\}} ${\mathit {A}}=\{Stanford,Stanley\}$ y B = { S t a n l e y , S t a n f o r d } {\mathit {B}}={Stanley,Stanford\}} ${\mathit {B}}=\{Stanley,Stanford\}$ , los conjuntos son los mismos.

Cardinalidad de un conjunto

Cuando los matemáticos hablan de un conjunto, a veces quieren saber cuán grande es un conjunto (o cuál es la cardinalidad del conjunto). Lo hacen contando cuántos elementos hay en el conjunto (cuántos elementos hay en la bolsa). Para los conjuntos finitos la cardinalidad es un número simple. El conjunto vacío tiene una cardinalidad de 0. El conjunto { a p l e , o r a n g e } $\{apple,orange\}$ {{manzana,naranja}} tiene una cardinalidad de 2.

Dos conjuntos tienen la misma cardinalidad si podemos emparejar sus elementos, es decir, si podemos unir dos elementos, uno de cada conjunto. El conjunto { a p l e , o r a n g e } {\displaystyle \ {manzana,naranja\}} $\{apple,orange\}$ y el conjunto { s u n , m o n } {\displaystyle \\\\\\Nde sol,luna\} $\{sun,moon\}$ tienen la misma cardinalidad. Por ejemplo, podríamos emparejar la manzana con el sol y la naranja con la luna. El orden no importa. Es posible emparejar todos los elementos, y ninguno queda fuera. Pero el conjunto { d o g , c a t , b i r d } {\displaystyle \{perro,gato,pájaro}} $\{dog,cat,bird\}$ y el conjunto {5 , 6 } {\displaystyle \{5,6\}} $\{5,6\}$ tienen diferente cardinalidad. Si intentamos emparejarlos, siempre dejamos fuera un animal.

Cardinalidad infinita

A veces la cardinalidad no es un número. A veces un conjunto tiene una cardinalidad infinita. El conjunto de todos los números enteros es un conjunto con cardinalidad infinita. Algunos conjuntos con cardinalidad infinita son más grandes (tienen una cardinalidad mayor) que otros. Hay más números reales que números naturales, por ejemplo, lo que significa que no podemos emparejar el conjunto de los números enteros y el conjunto de los números reales, aunque trabajemos eternamente.

Contabilidad

Si se pueden contar los elementos de un conjunto, éste se llama conjunto contable. Los conjuntos contables incluyen todos los conjuntos con un número finito de miembros. Los conjuntos contables también incluyen algunos conjuntos infinitos, como los números naturales. Se pueden contar los números naturales con 1 , 2 , 3... {\displaystyle {1,2,3...}} ${1,2,3...}$ . Los números naturales reciben el apodo de "los números para contar", ya que son los que solemos utilizar para contar cosas.

Un conjunto incontable es un conjunto infinito que es imposible de contar. Si intentamos contar los elementos, siempre nos saltaremos algunos. No importa el paso que demos. El conjunto de los números reales es un conjunto incontable. Hay muchos otros conjuntos incontables, incluso un intervalo tan pequeño como [ 0 , 1 ] {\displaystyle [0,1]} $[0,1]$ .[3]

Subconjuntos

Si se observa el conjunto A = { a , b } {\displaystyle A={a,b\}} $A=\{a,b\}$ y el conjunto B = {a , b , c , d } {\displaystyle B={a,b,c,d}} $B=\{a,b,c,d\}$ , se puede ver que todos los elementos del primer conjunto están también en el segundo.
Decimos: {a , b } {\displaystyle \ {a,b\}} $\{a,b\}$ es un subconjunto de { a , b , c , d } {\displaystyle \\\a,b,c,d\} $\{a,b,c,d\}$
Como fórmula tiene el siguiente aspecto
{ a , b } ⊆ { a , b $\{a,b\}\subseteq \{a,b,c,d\}$

En general, cuando todos los elementos del conjunto A {\displaystyle A} $A$ son también elementos del conjunto B {\displaystyle B} $B$ , llamamos a A {\displaystyle A} $A$ un subconjunto de B {\displaystyle B} : $B$
A ⊆ $A\subseteq B$ .
Suele leerse "A {\desde el estilo A} $A$ está contenido en B {\desde el estilo B} $B$ ."

Ejemplo: Todo Chevrolet es un coche americano. Así que el conjunto de todos los Chevrolet está contenido en el conjunto de todos los coches americanos.

Operaciones de ajuste

Hay diferentes formas de combinar los conjuntos.

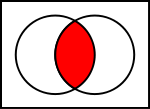
Intersecciones

La intersección A ∩ B {\cápitulo B} $A\cap B$ de dos conjuntos A {\cápitulo A} $A$ y B {\cápitulo B} $B$ es un conjunto que contiene todos los elementos que están a la vez en el conjunto A {\cápitulo A} $A$ y en el conjunto B {\cápitulo B} . $B$

Ejemplo: Cuando A {\displaystyle A} $A$ es el conjunto de todos los coches baratos, y B {\displaystyle B} $B$ es el conjunto de todos los coches americanos, entonces A ∩ B {\displaystyle A\cap B} $A\cap B$ es el conjunto de todos los coches americanos baratos.

Sindicatos

La unión A ∪ B {\cabeza de cartel B} $A\cup B$ de dos conjuntos A {\cabeza de cartel A} $A$ y B {\cabeza de cartel B} $B$ es un conjunto que contiene todos los elementos que están en el conjunto A {\cabeza de cartel A} $A$ o en el conjunto B {\cabeza de cartel B} $B$ . Esta "o" es la disyunción inclusiva, por lo que la unión también contiene los elementos, que están en el conjunto A {\displaystyle A} $A$ y en el conjunto B {\displaystyle B} $B$ . Por cierto, esto significa, que la intersección es un subconjunto de la unión: ( A ∩ B ) ⊆ ( A ∪ $(A\cap B)\subseteq (A\cup B)$ .

Ejemplo: Cuando A {\displaystyle A} $A$ es el conjunto de todos los coches baratos, y B {\displaystyle B} $B$ es el conjunto de todos los coches americanos, entonces A ∪ B {\displaystyle A\cup B} $A\cup B$ es el conjunto de todos los coches, sin todos los coches caros que no son de América.

Complementos

El complemento puede significar dos cosas diferentes:

El complemento de A {\año A} $A$ es el universo U {\año U} $U$ sin todos los elementos de A {\año A} $A$ :

A C = U ∖ A {\\año}=U\año}menos A} $A^{\rm {C}}=U\setminus A$
El universo U {\displaystyle U} $U$ es el conjunto de todas las cosas de las que se habla.
Ejemplo: Cuando U {\displaystyle U} $U$ es el conjunto de todos los coches, y A {\displaystyle A} $A$ es el conjunto de todos los coches baratos,
entonces A {\displaystyle A} $A$ ^C es el conjunto de todos los coches caros.

La diferencia de conjuntos de A {estilo A} $A$ y B {estilo B} $B$ es el conjunto B {estilo B} $B$ sin todos los elementos de A {estilo A} $A$ :

B ∖ A {\desde el estilo B\desde el punto de vista de A} $B\setminus A$
También se denomina complemento relativo de A {\displaystyle A} $A$ en B {\displaystyle B} $B$ .
Ejemplo: Cuando A {\displaystyle A} $A$ es el conjunto de todos los coches baratos, y B {\displaystyle B} $B$ es el conjunto de todos los coches americanos, entonces B ∖ A {\displaystyle B\setminus A} $B\setminus A$ es el conjunto de todos los coches americanos caros.

Si se intercambian los conjuntos en la diferencia de conjuntos, el resultado es diferente:
En el ejemplo de los coches, la diferencia A ∖ B {\displaystyle A\setminus B} $A\setminus B$ es el conjunto de todos los coches baratos, que no se fabrican en América.

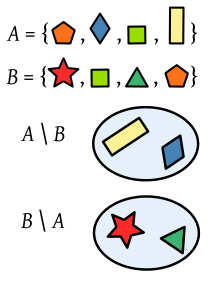
Diferencias de dos conjuntos de polígonos

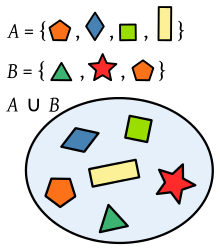
Unión de dos conjuntos de polígonos

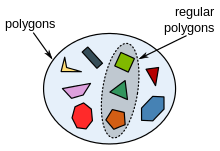
Un subconjunto de polígonos regulares

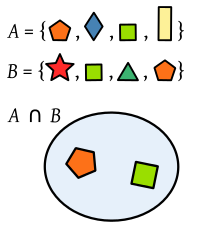
Intersección de dos conjuntos de polígonos

Notación

La mayoría de los matemáticos utilizan letras italianas mayúsculas (normalmente romanas) para escribir sobre los conjuntos (como A {\displaystyle A} $A$ , B {\displaystyle B} $B$ , C {\displaystyle C} $C$ ). Las cosas que se ven como elementos de conjuntos suelen escribirse con letras romanas minúsculas.

Una forma de mostrar un conjunto es mediante una lista de sus miembros, separados por comas, incluidos entre llaves. Por ejemplo,

X = { 1 , 2 , 3 } {\displaystyle X={1,2,3\}} $X=\{1,2,3\}$ es un conjunto que tiene los miembros 1, 2 y 3.

Otra forma, llamada notación de construcción de conjuntos, es mediante un enunciado de lo que es cierto de los miembros del conjunto, así:

{x | x es un número natural & x < 4}.

En inglés hablado, esto se lee: "el conjunto de todos los x tales que x es un número natural y x es menor que cuatro". El símbolo [ipe "|" significa "tal que" o "de modo que".

El conjunto vacío se escribe de una manera especial: ∅ {\displaystyle \\\\Nde vacíos} $\emptyset$ ∅ {\\Nde estilo de visualización \Nvarnothing} $\varnothing$ o {\Nde estilo de visualización \Nde vacío}. $\{\}$ .

Cuando el objeto a es el miembro del conjunto A {\dice A} $A$ se escribe como:

$a$ $\in$ $A$ .

En inglés hablado, esto se lee "a es un miembro de A {\año A} $A$ ".

Diagramas de Venn

Para ilustrar las operaciones sobre conjuntos los matemáticos utilizan los diagramas de Venn. Los diagramas de Venn utilizan círculos para mostrar conjuntos individuales. El conjunto se representa con un rectángulo. Los resultados de las operaciones se muestran como áreas coloreadas. En la ilustración de la operación de intersección, el círculo de la izquierda muestra el conjunto A {\año A} $A$ y el círculo de la derecha muestra el conjunto B {\año B} $B$ .

Intersección A ∩ B {\desde el punto de vista de A\cap B} $A\cap B$

Conjuntos especiales

Algunos conjuntos son muy importantes para las matemáticas. Se utilizan con mucha frecuencia. Uno de ellos es el conjunto vacío. Muchos de estos conjuntos especiales se escriben con letra de pizarra en negrita, y entre ellos se encuentran:

P {\displaystyle \mathbb {P} } $\mathbb {P}$ , denotando el conjunto de todos los primos.
N {\displaystyle \mathbb {N} } $\mathbb {N}$ , denotando el conjunto de todos los números naturales. Es decir, N {\displaystyle \mathbb {N} } $\mathbb {N}$ = {1, 2, 3, ...}, o a veces N {\displaystyle \mathbb {N} } $\mathbb {N}$ = {0, 1, 2, 3, ...}.
Z {\displaystyle \mathbb {Z} } $\mathbb {Z}$ , que denota el conjunto de todos los números enteros (ya sean positivos, negativos o cero). Así que Z {\displaystyle \mathbb {Z} } $\mathbb {Z}$ = {..., -2, -1, 0, 1, 2, ...}.
Q {\displaystyle \mathbb {Q} } $\mathbb {Q}$ , denotando el conjunto de todos los números racionales (es decir, el conjunto de todas las fracciones propias e impropias). Así, Q = { a b | a , b ∈ Z , b ≠ 0 } {\displaystyle \mathbb {Q} =\left{{comienzo{matriz}{frac {a}{b}{final{matriz}}|a,b\in \mathbb {Z} ,b\neq 0\right\} $\mathbb {Q} =\left\{{\begin{matrix}{\frac {a}{b}}\end{matrix}}|a,b\in \mathbb {Z} ,b\neq 0\right\}$ , es decir, todas las fracciones a b {\displaystyle {\begin{matrix}{frac {a}{b}}{end{matrix}}} ${\begin{matrix}{\frac {a}{b}}\end{matrix}}$ donde a y b están en el conjunto de todos los enteros y b no es igual a 0. Por ejemplo, 1 4 ∈ Q {\displaystyle {\begin{matrix}{frac {1}{4}}{end{matrix}}} en \mathbb {Q} } ${\begin{matrix}{\frac {1}{4}}\end{matrix}}\in \mathbb {Q}$ y 11 6 ∈ Q {\displaystyle {\begin{matrix}{frac {11}{6}}end{matrix}} en \mathbb {Q} } ${\begin{matrix}{\frac {11}{6}}\end{matrix}}\in \mathbb {Q}$ . Todos los números enteros están en este conjunto, ya que cada número entero a puede expresarse como la fracción a 1 {\displaystyle {\begin{matrix}{frac {a}{1}}\nd{matrix}} . ${\begin{matrix}{\frac {a}{1}}\end{matrix}}$
R {\displaystyle \mathbb {R} } $\mathbb {R}$ , que denota el conjunto de todos los números reales. Este conjunto incluye todos los números racionales, junto con todos los números irracionales (es decir, los números que no pueden reescribirse como fracciones, como π , {\displaystyle \pi ,} $\pi ,$ e , {\displaystyle e,} $e,$ y √2).
C {\displaystyle \mathbb {C} } $\mathbb {C}$ , denotando el conjunto de todos los números complejos.

Cada uno de estos conjuntos de números tiene un número infinito de elementos, y P ⊂ N ⊂ Z ⊂ Q ⊂ R ⊂ $\mathbb {P} \subset \mathbb {N} \subset \mathbb {Z} \subset \mathbb {Q} \subset \mathbb {R} \subset \mathbb {C}$ .

Paradojas sobre conjuntos

El matemático Bertrand Russell descubrió que hay problemas con la definición informal de los conjuntos. Lo expuso en una paradoja llamada la paradoja de Russell. Una versión más fácil de entender, más cercana a la vida real, se llama la paradoja de Barber.

La paradoja del barbero

Hay un pequeño pueblo en algún lugar. En ese pueblo hay un barbero. A todos los hombres del pueblo no les gusta la barba, así que o se afeitan ellos mismos, o van a la barbería para que el barbero les afeite.

Por tanto, podemos hacer una afirmación sobre el propio barbero: El barbero afeita a todos los hombres que no se afeitan a sí mismos. Sólo afeita a esos hombres (ya que los demás se afeitan solos y no necesitan que un barbero les dé un afeitado).

Esto, por supuesto, plantea la pregunta: ¿Qué hace el barbero cada mañana para parecer bien afeitado? Esta es la paradoja.

Si el barbero se afeita a sí mismo, no puede ser barbero, ya que un barbero no se afeita a sí mismo. Si no se afeita a sí mismo, entra en la categoría de los que no se afeitan a sí mismos, y por tanto, no puede ser barbero.

Páginas relacionadas

Conjunto Cantor
Teoría de grupos
Conjunto abierto
Relación
Teoría de conjuntos

Preguntas y respuestas

P: ¿Qué es un plató?

R: Un conjunto es una idea de las matemáticas. Está formado por miembros (también llamados elementos) que se definen por sus miembros, por lo que dos conjuntos con los mismos miembros son iguales.

P: ¿Puede un conjunto tener el mismo miembro más de una vez?

R: No, un conjunto no puede tener el mismo miembro más de una vez.

P: ¿Importa el orden en un conjunto?

R: No, el orden no importa en un conjunto. Cualquier cosa puede ser miembro de un conjunto, incluidos los propios conjuntos.

P: ¿Qué ocurre si un conjunto es miembro de sí mismo?

R: Si un conjunto es miembro de sí mismo, pueden producirse paradojas como la paradoja de Russell.

P: ¿Es la pertenencia lo único que importa para los conjuntos?

R: Sí, la pertenencia es lo único que importa para los conjuntos.

P: ¿Cómo se sabe si dos conjuntos son iguales?

R: Dos conjuntos son iguales si tienen los mismos miembros.