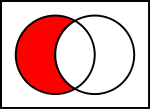
Diagrama de Venn: qué es, definición, historia y aplicaciones
Descubre qué es un Diagrama de Venn: definición, historia y aplicaciones prácticas en lógica, probabilidad y más. Explicaciones claras y ejemplos ilustrativos.
Un diagrama de Venn es un diagrama que muestra la relación lógica entre conjuntos. Fueron popularizados por John Venn en la década de 1880 y en la actualidad se utilizan ampliamente. Se emplean para enseñar la teoría elemental de conjuntos y para ilustrar relaciones simples entre conjuntos en probabilidad, lógica, estadística, lingüística e informática. Un diagrama de Venn utiliza curvas cerradas dibujadas en un plano para representar conjuntos; a menudo, estas curvas son círculos o elipses y se ubican dentro de un rectángulo que representa el conjunto universal (U).
Definición y elementos básicos
Un diagrama de Venn representa visualmente la relación entre conjuntos mediante regiones que corresponden a todas las combinaciones posibles de pertenencia o no pertenencia. Los elementos clave son:
- Conjuntos: representados por curvas cerradas (usualmente círculos) etiquetadas, por ejemplo A, B, C.
- Regiones: áreas en las que se intersectan o no los conjuntos; cada región corresponde a una combinación lógica (por ejemplo, A ∩ B pero no C).
- Conjunto universal (U): el rectángulo que contiene todos los elementos bajo consideración.
- Complemento: la región dentro de U pero fuera de un conjunto dado, representada como Ac o ¬A.
Operaciones habituales y cómo leerlas
Los diagramas de Venn facilitan la comprensión de operaciones entre conjuntos. Ejemplos comunes:
- Unión (A ∪ B): todas las regiones que pertenecen a A, a B o a ambas.
- Intersección (A ∩ B): la región donde A y B se solapan.
- Diferencia (A \ B): elementos en A pero no en B.
- Complemento (Ac): todo lo que está fuera de A dentro del universo U.
En probabilidad, por ejemplo, la regla de la unión para dos eventos se visualiza fácilmente: P(A ∪ B) = P(A) + P(B) − P(A ∩ B), porque la intersección queda contada dos veces si se suman P(A) y P(B).
Diagramas con dos, tres y más conjuntos
Los diagramas con dos conjuntos usan típicamente dos círculos que se solapan, creando tres regiones relevantes (solo A, solo B, A ∩ B). Con tres conjuntos se usan tres círculos que crean ocho regiones (2³): cada elemento del universo pertenece o no a cada uno de los tres conjuntos, de modo que todas las combinaciones posibles quedan representadas.
Para más de tres conjuntos la representación gráfica se vuelve más compleja; existen construcciones para diagramas de Venn simétricos con n conjuntos, pero son menos intuitivas. En la práctica, para muchos conjuntos se prefieren otras técnicas visuales o representaciones algebraicas.
Historia y diferencias con diagramas de Euler
Antes de Venn ya se habían propuesto ideas similares: Christian Weise en 1712 (Nucleus Logicoe Wiesianoe) y Leonhard Euler en Cartas a una princesa alemana (1768), por ejemplo, usaron figuras para representar relaciones entre conjuntos. John Venn popularizó y sistematizó estas representaciones en Lógica Simbólica, Capítulo V "Representación Diagramática", 1881.
Es importante distinguir diagramas de Venn de los diagramas de Euler. Mientras que los diagramas de Venn muestran todas las posibles regiones de intersección entre n conjuntos (incluso si algunas regiones están vacías), los diagramas de Euler omiten las regiones imposibles o vacías y dibujan solo las relaciones realmente existentes entre conjuntos. Por eso, los diagramas de Euler suelen ser más sencillos y más fieles a situaciones concretas, mientras que los de Venn son más útiles para estudiar todas las combinaciones lógicas posibles.
Aplicaciones prácticas
- En la enseñanza: ayudan a introducir conceptos de teoría de conjuntos y lógica proposicional de forma visual y didáctica.
- Probabilidad: para visualizar eventos y calcular probabilidades de uniones, intersecciones y complementos.
- Estadística y análisis de datos: para mostrar solapamientos de categorías, por ejemplo clientes que compran producto A, B y C.
- Lógica: equivalencias entre operaciones booleanas (AND, OR, NOT) y operaciones entre conjuntos.
- Informática: conceptos como operaciones sobre conjuntos, búsquedas en bases de datos, álgebra booleana y representación de permisos o características.
- Lingüística: para comparar campos semánticos, rasgos lingüísticos compartidos o distintivos entre lenguas y dialectos.
- Resolución de problemas y toma de decisiones: clarifican casos de solapamiento entre criterios o condiciones.
Convenciones y recursos visuales
Algunos usos y convenciones comunes:
- Etiquetar claramente cada conjunto (A, B, C...) y el universo (U).
- Usar sombreado o coloreado para indicar regiones específicas (por ejemplo, sombrear A ∩ B para enfatizar la intersección).
- Marcar con una X o con la palabra "vacío" las regiones que se sabe que no contienen elementos.
- Agregar conteos o probabilidades dentro de cada región para resolver problemas cuantitativos.
Limitaciones
Los diagramas de Venn son muy útiles para intuir relaciones sencillas, pero presentan limitaciones:
- Se vuelven difíciles de leer y de dibujar para más de tres o cuatro conjuntos.
- Representan todas las combinaciones posibles aunque muchas sean irrelevantes en un contexto real (a diferencia de los diagramas de Euler).
- No son ideales para datos con muchas categorías o con relaciones complejas que requieren visualizaciones alternativas (por ejemplo, matrices de intersección, diagramas de UpSet, gráficos de red).
Consejos prácticos para usar diagramas de Venn en ejercicios
- Identifica claramente el conjunto universal y las preguntas a responder (unión, intersección, diferencia, complemento).
- Cuenta o asigna valores a las regiones más específicas primero (por ejemplo, intersecciones de mayor orden) y luego suma según corresponda.
- Comprueba fórmulas básicas como: P(A ∪ B) = P(A) + P(B) − P(A ∩ B).
- Si hay más de tres conjuntos y el problema es puramente numérico, considera tablas de contingencia, álgebra booleana o herramientas informáticas en lugar de intentar dibujar todos los solapamientos.
En resumen, el diagrama de Venn es una herramienta visual poderosa y accesible para representar relaciones entre conjuntos y entender operaciones lógicas y probabilísticas. Su simplicidad lo hace ideal para la enseñanza y la resolución de problemas básicos, aunque para situaciones con muchos conjuntos o relaciones complejas conviene complementar con otras representaciones.

Vidriera en Cambridge, donde estudió John Venn. Muestra un diagrama de Venn.
Ejemplo
El siguiente ejemplo utiliza dos conjuntos, A y B, representados aquí como círculos de colores. El círculo naranja, conjunto A, representa a todos los seres vivos que tienen dos patas. El círculo azul, conjunto B, representa a los seres vivos que pueden volar. Cada tipo de criatura por separado puede imaginarse como un punto en algún lugar del diagrama. Las criaturas vivas que pueden tanto volar como tener dos patas -por ejemplo, los loros- están entonces en ambos conjuntos, y por tanto corresponden a puntos en el área donde los círculos azul y naranja se superponen. Esa zona contiene todos (y sólo) esos seres vivos.
Los humanos y los pingüinos son bípedos, y por tanto están en el círculo naranja, pero como no pueden volar, aparecen en la parte izquierda del círculo naranja, donde no se solapa con el círculo azul. Los mosquitos tienen seis patas y vuelan, por lo que el punto de los mosquitos está en la parte del círculo azul que no se solapa con el naranja. Las criaturas que no tienen dos patas y no pueden volar (por ejemplo, las ballenas y las arañas) estarían representadas por puntos fuera de ambos círculos.
El área combinada de los conjuntos A y B se llama la unión de A y B, denotada por A ∪ B. La unión en este caso contiene todos los seres vivos que tienen dos patas o que pueden volar (o ambos). El área en A y B, donde los dos conjuntos se superponen, se llama la intersección de A y B, denotada por A ∩ B. Por ejemplo, la intersección de los dos conjuntos no está vacía, porque hay puntos que representan criaturas que están tanto en el círculo naranja como en el azul.
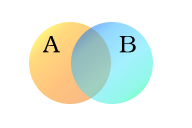
Conjuntos A (criaturas con dos patas) y B (criaturas que pueden volar)
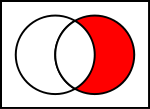
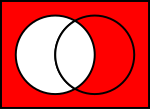
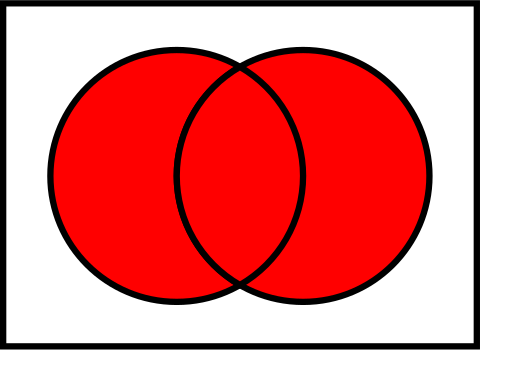
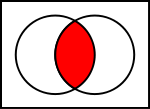
Diagramas de Venn de operaciones comunes sobre conjuntos
En las ilustraciones de abajo, el círculo de la izquierda muestra el conjunto 

Páginas relacionadas
- Disyunción exclusiva
- Disyunción inclusiva
Preguntas y respuestas
P: ¿Qué es un diagrama de Venn?
R: Un diagrama de Venn es un diagrama que muestra la relación lógica entre conjuntos. Utiliza curvas cerradas dibujadas en un plano, normalmente círculos o elipses, para representar conjuntos.
P: ¿Quién popularizó los diagramas de Venn?
R: John Venn popularizó los diagramas de Venn en la década de 1880.
P: ¿Para qué se utilizan?
R: Se utilizan para enseñar la teoría elemental de conjuntos y para ilustrar relaciones simples entre conjuntos en probabilidad, lógica, estadística, lingüística e informática.
P: ¿Quién propuso ideas similares antes de John Venn?
R: Christian Weise propuso ideas similares en 1712 con su Nucleus Logicoe Wiesianoe y Leonhard Euler las propuso en Cartas a una princesa alemana en 1768.
P: ¿Cuándo publicó John Venn la Lógica Simbólica?
R: John Venn publicó Lógica Simbólica en 1881.
P: ¿En qué capítulo de Lógica Simbólica popularizó John Venn la idea de un diagrama de Venn?
R: La idea de un diagrama de Venn fue popularizada por John Venn en el capítulo 5 "Representación diagramática" de la Lógica Simbólica.
P: ¿Cómo se representaban estas ideas antes de la invención de la versión moderna del diagrama deV enn?
R: Antes de la invención de la versión moderna del diagrama deV enn, estas ideas se representaban mediante curvas cerradas dibujadas en un plano, como círculos o elipses.
Buscar dentro de la enciclopedia