Estadística | rama de las matemáticas aplicadas que se ocupa de la recogida, organización, análisis, lectura y presentación de datos
La estadística es una rama de las matemáticas aplicadas que se ocupa de la recogida, organización, análisis, lectura y presentación de datos. La estadística descriptiva hace resúmenes de los datos. La estadística inferencial hace predicciones. La estadística ayuda en el estudio de muchos otros campos, como la ciencia, la medicina, la economía, la psicología, la política y el marketing. Alguien que trabaja en estadística se llama estadístico. Además de ser el nombre de un campo de estudio, la palabra "estadística" también puede significar números que se utilizan para describir datos o relaciones.
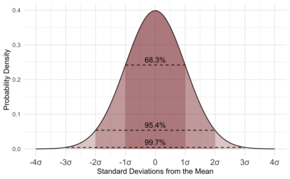
La distribución normal en Estadística
Historia
Las primeras estadísticas conocidas son los datos del censo. Los babilonios hicieron un censo hacia el 3500 a.C., los egipcios hacia el 2500 a.C. y los antiguos chinos hacia el 1000 a.C.
A partir del siglo XVI, matemáticos como Gerolamo Cardano desarrollaron la teoría de la probabilidad, que convirtió la estadística en una ciencia. Desde entonces, la gente ha recogido y estudiado las estadísticas de muchas cosas. Los árboles, las estrellas de mar, las rocas, las palabras, casi cualquier cosa que pueda contarse ha sido objeto de estadística.
Recogida de datos
Antes de poder describir el mundo con la estadística, debemos recoger datos. Los datos que recogemos en estadística se llaman mediciones. Después de recoger los datos, utilizamos uno o más números para describir cada observación o medición. Por ejemplo, supongamos que queremos averiguar la popularidad de un determinado programa de televisión. Podemos elegir un grupo de personas (llamado muestra) de la población total de espectadores. Entonces preguntamos a cada espectador de la muestra con qué frecuencia ve el programa. La muestra son datos que se pueden ver, y la población son datos que no se pueden ver (suponiendo que no se pregunte a todos los espectadores de la población). Por otro ejemplo, si queremos saber si un determinado medicamento puede ayudar a reducir la presión arterial, podríamos administrar el medicamento a las personas durante algún tiempo y medir su presión arterial antes y después.
Estadísticas descriptivas e inferenciales
Los números que describen los datos que uno puede ver se llaman estadísticas descriptivas. Los números que hacen predicciones sobre los datos que uno no puede ver se llaman estadísticas inferenciales.
La estadística descriptiva consiste en utilizar números para describir características de los datos. Por ejemplo, la estatura media de las mujeres en Estados Unidos es una estadística descriptiva: describe una característica (la estatura media) de una población (las mujeres en Estados Unidos).
Una vez que los resultados se han resumido y descrito, pueden utilizarse para la predicción. Esto se llama estadística inferencial. Como ejemplo, el tamaño de un animal depende de muchos factores. Algunos de estos factores están controlados por el entorno, pero otros lo son por la herencia. Por lo tanto, un biólogo podría hacer un modelo que diga que hay una alta probabilidad de que la descendencia sea de tamaño pequeño, si los padres eran de tamaño pequeño. Este modelo permite probablemente predecir el tamaño de mejor manera que simplemente adivinando al azar. La comprobación de si un determinado fármaco puede servir para curar una determinada afección o enfermedad suele hacerse comparando los resultados de las personas a las que se les administra el fármaco con las que reciben un placebo.
Métodos
La mayoría de las veces, recogemos datos estadísticos haciendo encuestas o experimentos. Por ejemplo, un sondeo de opinión es un tipo de encuesta. Elegimos a un pequeño número de personas y les hacemos preguntas. Luego, utilizamos sus respuestas como datos.
La elección de los individuos que se toman para una encuesta o una recogida de datos es importante, ya que influye directamente en las estadísticas. Cuando las estadísticas están hechas, ya no se puede determinar qué individuos se toman. Supongamos que queremos medir la calidad del agua de un gran lago. Si tomamos muestras junto al desagüe, obtendremos resultados diferentes que si las muestras se toman en un lugar alejado y de difícil acceso del lago.
Hay dos tipos de problemas que se suelen encontrar al tomar muestras:
- Si hay muchas muestras, es probable que éstas se aproximen mucho a lo que son en la población real. Sin embargo, si hay muy pocas muestras, podrían ser muy diferentes de lo que son en la población real. Este error se denomina error de azar (véase también Errores y residuos en estadística).
- Los individuos para las muestras deben ser elegidos cuidadosamente. Por lo general, se elegirán al azar. Si no es así, las muestras podrían ser muy diferentes de lo que realmente son en la población total. Esto es así incluso si se toma un gran número de muestras. Este tipo de error se denomina sesgo.
Errores
Podemos reducir los errores de azar tomando una muestra más grande, y podemos evitar algunos sesgos eligiendo al azar. Sin embargo, a veces es difícil tomar grandes muestras aleatorias. Y el sesgo puede producirse si no se pregunta a diferentes personas, o si éstas se niegan a responder a nuestras preguntas, o si saben que están recibiendo un tratamiento falso. Estos problemas pueden ser difíciles de solucionar. Consulte el error estándar para saber más.
Estadísticas descriptivas
Encontrar el centro de los datos
El punto medio de los datos se denomina media. La media nos habla de un individuo típico de la población. Hay tres tipos de media que se suelen utilizar: la media, la mediana y la moda.
Los ejemplos siguientes utilizan estos datos de muestra:
| Nombre | A | B | C | D | E | F | G | H | I | J |
| Puntuación | 23 | 26 | 49 | 49 | 57 | 64 | 66 | 78 | 82 | 92 |
Media
La fórmula de la media es
Donde 

Esto significa que se calcula la media sumando todos los valores, y luego se divide por el número de valores. Para el ejemplo anterior, la media es:
El problema de la media es que no dice nada sobre cómo se distribuyen los valores. Los valores que son muy grandes o muy pequeños cambian mucho la media. En estadística, estos valores extremos pueden ser errores de medición, pero a veces la población contiene realmente estos valores. Por ejemplo, si en una sala hay 10 personas que ganan 10 dólares al día y 1 que gana 1.000.000 de dólares al día. La media de los datos es de 90.918 dólares al día. Aunque es la cantidad media, la media en este caso no es la cantidad que gana una sola persona, y por tanto no es muy útil para algunos propósitos.
La media descrita anteriormente es la "media aritmética". Otros tipos son útiles para algunos fines.
Mediana
La mediana es el elemento medio de los datos. Para un dato 

Como otro ejemplo, como el de los ingresos presentado para la media, considere una habitación con 10 personas que tienen ingresos de 10, 20, 20, 40, 50, 60, 90, 90, 100 y 1.000.000 de dólares. En este caso, la mediana es $55, porque $55 es la media de los dos números centrales, $50 y $60. Si se ignora el valor extremo de 1.000.000 de dólares, la media es de 53. En este caso, la mediana se aproxima al valor obtenido cuando se descarta el valor extremo. La mediana resuelve el problema de los valores extremos descrito en la definición de media anterior.
Modo
La moda es el elemento más frecuente de los datos. Por ejemplo, la letra más común en inglés es la "e". Diríamos que la "e" es la moda de la distribución de las letras.
Como otro ejemplo, si hay 10 personas en una habitación con ingresos de 10, 20, 20, 40, 50, 60, 90, 90, 90, 100 y 1.000.000 de dólares, entonces la moda es 90, porque 90 aparece tres veces y todos los demás valores aparecen menos de tres veces.
Puede haber más de un modo. Por ejemplo, si hay 10 personas en una habitación con ingresos de 10, 20, 20, 20, 50, 60, 90, 90, 100 y 1.000.000 de dólares, los modos son 20 y 90 dólares. Esto es bimodal, o tiene dos modos. La bimodalidad es muy común, y a menudo indica que los datos son la combinación de dos grupos diferentes. Por ejemplo, la altura media de todos los adultos de EE.UU. tiene una distribución bimodal. Esto se debe a que los hombres y las mujeres tienen alturas medias separadas de 1,763 m (5 pies 9 + 1⁄2 pulgadas) para los hombres y 1,622 m (5 pies 4 pulgadas) para las mujeres. Estos picos son evidentes cuando se combinan ambos grupos.
La moda es la única forma de media que puede utilizarse para los datos que no pueden ordenarse.
Encontrar la dispersión de los datos
Otra cosa que podemos decir de un conjunto de datos es su dispersión. Una forma habitual de describir la dispersión de un conjunto de datos es la desviación estándar. Si la desviación estándar de un conjunto de datos es pequeña, entonces la mayoría de los datos están muy cerca de la media. Sin embargo, si la desviación estándar es grande, entonces muchos de los datos son muy diferentes de la media.
La desviación estándar de una muestra suele ser diferente de la desviación estándar de su población de origen . Por ello, escribimos σ 

Si los datos siguen el patrón común llamado distribución normal, entonces es muy útil conocer la desviación estándar. Si los datos siguen este patrón (diríamos que los datos están distribuidos normalmente), alrededor de 68 de cada 100 datos se desviarán de la media en menos de la desviación estándar. No sólo eso, sino que alrededor de 95 de cada 100 mediciones estarán fuera de la media por menos de dos veces la desviación estándar, y alrededor de 997 de cada 1000 estarán más cerca de la media por menos de tres desviaciones estándar.
Otras estadísticas descriptivas
También podemos utilizar la estadística para averiguar que algún porcentaje, percentil, número o fracción de personas o cosas de un grupo hacen algo o encajan en una categoría determinada.
Por ejemplo, los científicos sociales utilizaron las estadísticas para averiguar que el 49% de las personas del mundo son hombres.
Software relacionado
Para ayudar a los estadísticos, se han desarrollado muchos programas informáticos de estadística:
- MATLAB
- R
- Instituto SAS
- SPSS (fabricado por IBM)
Preguntas y respuestas
P: ¿Qué es la estadística?
R: La estadística es una rama de las matemáticas aplicadas que se ocupa de la recogida, organización, análisis, lectura y presentación de datos.
P: ¿Cuáles son los dos tipos de estadística?
R: Los dos tipos de estadística son la descriptiva y la inferencial. La estadística descriptiva hace resúmenes de los datos mientras que la inferencial hace predicciones.
P: ¿Cómo ayuda la estadística en otros campos?
R: La estadística ayuda en el estudio de muchos otros campos como la ciencia, la medicina, la economía, la psicología, la política y el marketing.
P: ¿Quién trabaja en el campo de la estadística?
R: Alguien que trabaja en el campo de la estadística se llama estadístico.
P: ¿Qué significa la palabra "estadística"?
R: Además de ser el nombre de un campo de estudio, la palabra "estadística" también puede significar números que se utilizan para describir datos o relaciones.
P: ¿A qué actividades se dedican los estadísticos?
R: Los estadísticos se dedican a actividades como la recopilación, organización, análisis, lectura y presentación de datos.
Buscar dentro de la enciclopedia

