Desviación típica | es un número que se utiliza para indicar la dispersión de las mediciones de un grupo con respecto a la media
La desviación estándar es un número que se utiliza para indicar la dispersión de las mediciones de un grupo con respecto a la media (valor medio o esperado). Una desviación estándar baja significa que la mayoría de los números están cerca de la media, mientras que una desviación estándar alta significa que los números están más dispersos.
El margen de error comunicado suele ser el doble de la desviación estándar. Los científicos suelen informar de la desviación estándar de los números respecto al número medio en los experimentos. A menudo deciden que sólo son importantes las diferencias superiores a dos o tres veces la desviación estándar. La desviación estándar también es útil en el dinero, donde la desviación estándar sobre los intereses ganados muestra lo diferente que puede ser el interés ganado por una persona respecto a la media.
Muchas veces, sólo se puede medir una muestra, o parte de un grupo. Entonces se puede hallar un número cercano a la desviación estándar de todo el grupo mediante una ecuación ligeramente diferente llamada desviación estándar de la muestra, que se explica a continuación. En este caso, la desviación estándar de todo el grupo se representa con la letra griega σ 

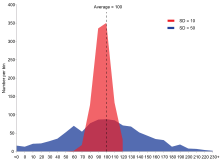
Ejemplo de dos poblaciones de muestra con la misma media y diferentes desviaciones estándar. La población roja tiene una media de 100 y una DE de 10; la población azul tiene una media de 100 y una DE de 50.
.png)
Un gráfico de una distribución normal (o curva de campana). Cada banda de color tiene una anchura de una desviación estándar.
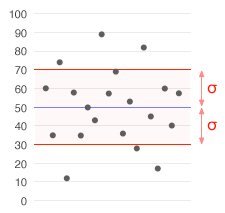
Un conjunto de datos con una media de 50 (mostrada en azul) y una desviación estándar (σ) de 20.
Ejemplo básico
Considere un grupo que tiene los siguientes ocho números:
Estos ocho números tienen una media de 5:
Para calcular la desviación típica de la población, encuentre primero la diferencia de cada número de la lista con respecto a la media. Luego eleve al cuadrado el resultado de cada diferencia:
A continuación, encuentre la media de estos valores (suma dividida por el número de números). Por último, saque la raíz cuadrada:
La respuesta es la desviación estándar de la población. La fórmula sólo es cierta si los ocho números con los que empezamos son todo el grupo. Si sólo son una parte del grupo elegida al azar, entonces podemos obtener una estimación no sesgada de cuál es la desviación estándar de la población dividiendo por 7 (que es n - 1) en lugar de 8 (que es n) en la parte inferior (denominador) de la fórmula anterior. Entonces la respuesta es la desviación típica de la muestra (corregida por el sesgo). Esto se llama la corrección de Bessel. A menudo utilizamos esta corrección porque la varianza de la muestra, es decir, el cuadrado de la desviación típica de la muestra, es un estimador insesgado de la varianza de la población, en otras palabras, el valor esperado o la media a largo plazo de la varianza de la muestra es igual a la varianza de la población (verdadera). Sin embargo, no es cierto que la desviación típica de la muestra sea un estimador insesgado de la desviación típica de la población[1]. Aunque la corrección de Bessel es una estimación insesgada de la varianza, esta estimación tiene un error cuadrático medio más elevado que la estimación sesgada o, en otras palabras, la estimación sesgada (es decir, dividida por n en lugar de n-1) está, por término medio, más cerca del valor verdadero.
Más ejemplos
He aquí un ejemplo un poco más difícil de la vida real: La altura media de los hombres adultos en Estados Unidos es de 70", con una desviación estándar de 3". Una desviación estándar de 3" significa que la mayoría de los hombres (alrededor del 68%, suponiendo una distribución normal) tienen una altura de 3" más alta a 3" más baja que la media (67"-73") - una desviación estándar. Casi todos los hombres (alrededor del 95%) tienen una altura de 6" más alta a 6" más baja que la media (64"-76") - dos desviaciones estándar. Tres desviaciones estándar incluyen todos los números del 99,7% de la muestra de población estudiada. Esto es cierto si la distribución es normal (en forma de campana).
Si la desviación estándar fuera cero, entonces todos los hombres medirían exactamente 70". Si la desviación estándar fuera de 20", entonces algunos hombres serían mucho más altos o mucho más bajos que la media, con un rango típico de aproximadamente 50"-90".
Para otro ejemplo, cada uno de los tres grupos {0, 0, 14, 14}, {0, 6, 8, 14} y {6, 6, 8, 8} tiene una media (promedio) de 7. Pero sus desviaciones típicas son 7, 5 y 1. El tercer grupo tiene una desviación típica mucho menor que los otros dos porque sus números son todos cercanos a 7. En general, la desviación típica nos dice lo lejos que tienden a estar el resto de los números de la media, y tendrá las mismas unidades que los propios números. Si, por ejemplo, el grupo {0, 6, 8, 14} son las edades de un grupo de cuatro hermanos en años, la media es de 7 años y la desviación típica es de 5 años.
La desviación estándar puede servir como medida de incertidumbre. En la ciencia, por ejemplo, la desviación estándar de un grupo de mediciones repetidas ayuda a los científicos a saber lo seguros que están del número medio. A la hora de decidir si las mediciones de un experimento coinciden con una predicción, la desviación estándar de esas mediciones es muy importante. Si el número medio de los experimentos se aleja demasiado del número predicho (con la distancia medida en desviaciones estándar), entonces la teoría que se está probando puede no ser correcta. Para más información, consulte el intervalo de predicción.
Ejemplos de aplicación
La comprensión de la desviación estándar de un conjunto de valores nos permite conocer la magnitud de la diferencia con respecto a la "media" (promedio).
El tiempo
Como ejemplo sencillo, considere las temperaturas máximas diarias medias de dos ciudades, una del interior y otra cercana al océano. Es útil entender que el rango de temperaturas altas diarias de las ciudades cercanas al océano es menor que el de las ciudades del interior. Estas dos ciudades pueden tener cada una la misma temperatura alta diaria media. Sin embargo, la desviación estándar de la temperatura alta diaria de la ciudad costera será menor que la de la ciudad del interior.
Deportes
Otra forma de verlo es considerar los equipos deportivos. En cualquier deporte, habrá equipos que sean buenos en algunas cosas y en otras no. Los equipos mejor clasificados no mostrarán muchas diferencias en sus habilidades. Lo hacen bien en la mayoría de las categorías. Cuanto menor sea la desviación estándar de su capacidad en cada categoría, más equilibrados y consistentes serán. Sin embargo, los equipos con una desviación estándar más alta serán menos predecibles. Un equipo que suele ser malo en la mayoría de las categorías tendrá una desviación típica baja. Un equipo que suele ser bueno en la mayoría de las categorías también tendrá una desviación típica baja. Sin embargo, un equipo con una desviación típica alta podría ser el tipo de equipo que anota muchos puntos (fuerte ataque) pero que también deja que el otro equipo anote muchos puntos (débil defensa).
Tratar de saber con antelación qué equipos ganarán puede incluir mirar las desviaciones estándar de las distintas "estadísticas" de los equipos. Los números que difieren de los esperados pueden equiparar los puntos fuertes con los débiles para mostrar qué razones pueden ser más importantes para saber qué equipo ganará.
En las carreras, se mide el tiempo que tarda un piloto en terminar cada vuelta alrededor de la pista. Un piloto con una baja desviación estándar de los tiempos de vuelta es más consistente que un piloto con una desviación estándar más alta. Esta información puede utilizarse para ayudar a entender cómo un conductor puede reducir el tiempo para terminar una vuelta.
Dinero
En dinero, la desviación estándar puede significar el riesgo de que un precio suba o baje (acciones, bonos, propiedades, etc.). También puede significar el riesgo de que un grupo de precios suba o baje (fondos de inversión gestionados activamente, fondos de inversión indexados o ETF). El riesgo es una razón para tomar decisiones sobre qué comprar. El riesgo es un número que la gente puede utilizar para saber cuánto dinero puede ganar o perder. A medida que el riesgo aumenta, el rendimiento de una inversión puede ser mayor de lo esperado (la desviación estándar "más"). Sin embargo, una inversión también puede perder más dinero del esperado (la desviación típica "menos").
Por ejemplo, una persona tiene que elegir entre dos acciones. La acción A durante los últimos 20 años tuvo un rendimiento medio del 10 por ciento, con una desviación estándar de 20 puntos porcentuales (pp). La acción B durante los últimos 20 años tuvo un rendimiento medio del 12 por ciento, pero una desviación estándar mayor, de 30 pp. Pensando en el riesgo, la persona puede decidir que la acción A es la opción más segura. Aunque no gane tanto dinero, probablemente tampoco perderá mucho dinero. La persona puede pensar que la media de 2 puntos más alta de la Acción B no merece la pena la desviación estándar adicional de 10 pp (mayor riesgo o incertidumbre del rendimiento esperado).
Reglas para números con distribución normal
La mayoría de las ecuaciones matemáticas para la desviación estándar suponen que los números están distribuidos normalmente. Esto significa que los números están repartidos de una forma determinada a ambos lados del valor medio. La distribución normal también se llama distribución gaussiana porque fue descubierta por Carl Friedrich Gauss. A menudo se le llama curva de campana porque los números se extienden para dar la forma de una campana en un gráfico.
Los números no están distribuidos normalmente si se agrupan a un lado o al otro del valor medio. Los números pueden estar dispersos y seguir teniendo una distribución normal. La desviación estándar indica la amplitud de la dispersión de los números.

El azul oscuro es menos de una desviación estándar de la media. Para la distribución normal, esto incluye el 68,27% de los números; mientras que dos desviaciones estándar de la media (azul medio y oscuro) incluyen el 95,45%; tres desviaciones estándar (azul claro, medio y oscuro) incluyen el 99,73%; y cuatro desviaciones estándar representan el 99,994%.
Relación entre la media (promedio) y la desviación estándar
La media (promedio) y la desviación estándar de un conjunto de datos suelen escribirse juntas. Así, una persona puede entender cuál es el número medio y la dispersión de los demás números del grupo.
La forma en que se reparte un grupo de números también puede venir dada por el coeficiente de variación (CV), que es la desviación estándar dividida por la media. Es un número adimensional. El coeficiente de variación se suele multiplicar por el 100% y se escribe como porcentaje.
Historia
El término desviación estándar fue utilizado por primera vez por escrito por Karl Pearson en 1894, después de utilizarlo en conferencias. Fue como una sustitución de nombres anteriores para la misma idea: por ejemplo, Gauss utilizaba el error medio.
Páginas relacionadas
- Exactitud y precisión
- Tamaño de la muestra
- Error estándar
- Varianza
Preguntas y respuestas
P: ¿Qué es la desviación estándar?
R: La desviación estándar es un número que se utiliza para indicar la dispersión de las mediciones de un grupo con respecto a la media (valor medio o esperado).
P: ¿Qué significa una desviación estándar baja?
R: Una desviación típica baja significa que la mayoría de las cifras se acercan a la media.
P: ¿Qué significa una desviación típica alta?
R: Una desviación típica alta significa que los números están más dispersos.
P: ¿Cómo se utiliza la desviación típica en el dinero?
R: En el dinero, la desviación típica de los intereses ganados muestra la diferencia entre los intereses ganados por una persona y la media.
P: ¿Cuándo se puede medir sólo una parte de un grupo?
R: Muchas veces, sólo se puede medir una muestra, o parte de un grupo.
P: ¿Cómo se representa la desviación típica de todo el grupo?
R: La desviación estándar de todo el grupo se representa con la letra griega ף {\displaystyle \sigma } .
P: ¿Cómo se representa la desviación típica de la muestra?
R: La desviación estándar de la muestra se representa por s {\displaystyle s} .
Buscar dentro de la enciclopedia



