Función exponencial | función que crece más y más rápido
En matemáticas, la función exponencial es una función que crece cada vez más rápido. Más precisamente, es la función 
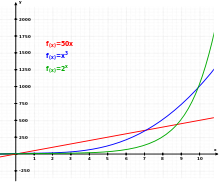
Tres funciones diferentes: Lineal (rojo), Cúbica (azul) y Exponencial (verde).
Propiedades
Dado que las funciones exponenciales utilizan la exponenciación, siguen las mismas reglas de los exponentes. Así,

Esto sigue la regla de que 
El logaritmo natural es la operación inversa de una función exponencial, donde:
La función exponencial satisface una propiedad interesante e importante en el cálculo diferencial:
Esto significa que la pendiente de la función exponencial es la propia función exponencial, y como resultado tiene una pendiente de 1 en 
Aplicaciones
La función exponencial general, en la que la base no es necesariamente 
Un ejemplo de función exponencial en la vida real sería el interés en un banco. Si una persona deposita 100 libras esterlinas en una cuenta que obtiene un 3% de interés al mes, entonces el saldo de cada mes (suponiendo que el dinero no se toca) sería el siguiente:
| Mes | Balance | Mes | Balance |
| Enero | £100.00 | Julio | £119.41 |
| Febrero | £103.00 | Agosto | £122.99 |
| Marzo | £106.09 | Septiembre | £126.68 |
| Abril | £109.27 | Octubre | £130.48 |
| Mayo | £112.55 | Noviembre | £134.39 |
| Junio | £115.93 | Diciembre | £138.42 |
Aquí, fíjese en cómo el dinero extra de los intereses aumenta cada mes, ya que cuanto mayor sea el saldo original, más intereses obtendrá la persona.
A continuación se muestran dos ejemplos matemáticos de funciones exponenciales (con base a).
| a=2
| a=3
|
Relación con la constante matemática e
Aunque la base ( 
El número e es importante para toda función exponencial. Por ejemplo, un banco paga un interés del 0,01% cada día. Una persona coge el dinero de los intereses y lo mete en una caja. Después de 10.000 días (unos 30 años), tiene 2 veces más dinero que con el que empezó. Otra persona coge su dinero de los intereses y lo vuelve a meter en el banco. Como el banco le paga ahora los intereses, la cantidad de dinero es una función exponencial.
De hecho, después de 10.000 días, no tiene 2 veces más dinero que al principio, pero tiene 2,718145 veces más dinero que al principio. Este número está muy cerca del número e. Si el banco paga los intereses más a menudo, de modo que la cantidad pagada cada vez es menor, entonces el número estará más cerca del número e.
Una persona también puede mirar la imagen para ver por qué el número e es importante para las funciones exponenciales. La imagen tiene tres curvas diferentes. La curva con los puntos negros es una función exponencial con una base ligeramente menor que e. La curva con las líneas negras cortas es una función exponencial con una base ligeramente mayor que e. La curva azul es una función exponencial con una base exactamente igual a e. La línea roja es una tangente a la curva azul. Toca la curva azul en un punto sin cruzarla. Una persona puede ver que la curva roja cruza el eje x, la línea que va de izquierda a derecha en -1. Esto es cierto sólo para la curva azul. Esta es la razón por la que la función exponencial de base e es especial.
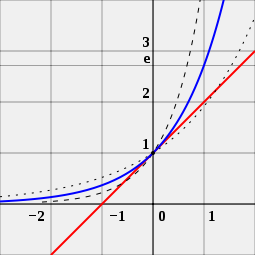
e es el único número a, tal que el valor de la derivada de la función exponencial f (x) = ax (curva azul) en el punto x = 0 es exactamente 1. Para comparar, se muestran las funciones 2x (curva punteada) y 4x (curva discontinua), que no son tangentes a la línea de pendiente 1 (roja).
Páginas relacionadas
Preguntas y respuestas
P: ¿Qué es la función exponencial?
R: La función exponencial es una función matemática que crece cada vez más rápido.
P: ¿Cómo se expresa matemáticamente la función exponencial?
R: La función exponencial se expresa matemáticamente como exp(x) = e^x, donde e es la constante de Euler.
P: ¿Qué representa la constante de Euler?
R: La constante de Euler representa un número irracional que es aproximadamente 2,71828.
P: ¿La función exponencial es siempre creciente?
R: Sí, la función exponencial siempre aumenta su valor a medida que aumenta x.
P: ¿Existe algún límite a la rapidez con la que puede crecer la función exponencial?
R: No, no hay límite a la rapidez con la que puede crecer la función exponencial, ya que sigue aumentando con valores mayores de x.
P: ¿Cómo podemos calcular la constante de Euler?
R: Podemos calcular la constante de Euler utilizando métodos numéricos como las series de Taylor o las fracciones continuas.
P: ¿Qué otras aplicaciones tiene la función exponencial además de las matemáticas?
R: La función exponencial tiene muchas aplicaciones fuera de las matemáticas, como la física, la química, la biología, la economía y la ingeniería.
Buscar dentro de la enciclopedia


