AlegsaOnline.com

Cálculo diferencial | el estudio de averiguar la tasa de cambio de una variable

Autor: Leandro Alegsa

24-11-2022

El cálculo diferencial, una rama del cálculo, es el estudio de averiguar la tasa de cambio de una variable en comparación con otra variable, mediante el uso de funciones. Es una forma de averiguar cómo cambia una forma de un punto a otro, sin necesidad de dividir la forma en un número infinito de piezas. El cálculo diferencial es lo contrario del cálculo integral. Fue desarrollado en las décadas de 1670 y 1680 por Sir Isaac Newton y Gottfried Leibniz.

Antecedentes

A diferencia de un número como 5 o 200, una variable puede cambiar su valor. Por ejemplo, la distancia y el tiempo son variables. En una carrera olímpica, a medida que la persona corre, su distancia desde la línea de salida aumenta. Mientras tanto, un cronómetro o un reloj miden el tiempo a medida que va subiendo. Podemos medir la velocidad media del corredor, si dividimos la distancia que recorrió por el tiempo que tardó. Pero esto no dice a qué velocidad corría la persona exactamente a 1,5 segundos de la carrera. Si tuviéramos la distancia a 1 segundo y la distancia a 2 segundos, seguiríamos teniendo sólo una media, aunque probablemente sería más correcta que la media de toda la carrera.

Hasta que se inventó el cálculo, la única forma de calcular esto era cortar el tiempo en trozos cada vez más pequeños, de forma que la velocidad media a lo largo del tiempo más pequeño se acercara cada vez más a la velocidad real en exactamente 1,5 segundos. Este era un proceso muy largo y difícil, y había que hacerlo cada vez que se quería calcular algo. Ciertamente, es mucho más difícil para un conductor averiguar la velocidad de un coche utilizando únicamente su cuentakilómetros (medidor de distancia) y su reloj, sin un velocímetro.

Un problema muy similar es hallar la pendiente (lo empinada que es) en cualquier punto de una curva. La pendiente de una línea recta es fácil de calcular: es simplemente cuánto sube (y o vertical) dividido por cuánto cruza (x u horizontal). Si una recta es paralela al eje x, su pendiente es cero. Si una línea recta pasa por (x,y) = (2,10) y (4,18), la línea sube 8 y atraviesa 2, por lo que su pendiente es 8 dividido 2, que es 4.

En una "curva", sin embargo, la pendiente es una variable (tiene diferentes valores en diferentes puntos), porque la línea se curva. Pero si la curva se cortara en trozos muy, muy pequeños, la curva en el punto se vería casi como una línea recta muy corta. Así que para calcular su pendiente, se puede trazar una línea recta que pase por el punto con la misma pendiente que la curva en ese punto. Si se hace exactamente así, la recta tendrá la misma pendiente que la curva, y se llama tangente. Pero no hay forma de saber (sin cálculo) si la tangente es exactamente correcta, y nuestros ojos no son lo suficientemente precisos como para estar seguros de si es exacta o simplemente muy cercana.

Lo que Newton y Leibniz encontraron fue una forma de calcular la pendiente (o la velocidad en el ejemplo de la distancia) con exactitud, utilizando reglas simples y lógicas. Dividieron la curva en un número infinito de trozos muy pequeños. Entonces eligieron puntos a ambos lados del punto que les interesaba y calcularon las tangentes en cada uno de ellos. A medida que los puntos se acercaban hacia el punto que les interesaba, la pendiente se aproximaba a un valor particular a medida que las tangentes se acercaban a la pendiente real de la curva. Dijeron que este valor particular al que se acercaba era la pendiente real.

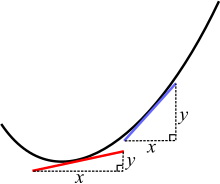
En una curva, dos puntos diferentes tienen pendientes distintas. Las líneas roja y azul son tangentes a la curva.

Cómo funciona

Digamos que tenemos una función y = f(x). f es la abreviatura de función, por lo que esta ecuación significa "y es una función de x". Esto nos dice que la altura de y en el eje vertical depende de lo que sea x (el eje horizontal) en ese momento. Por ejemplo, con la ecuación y = x², sabemos que si x es 1, entonces y será 1; si x es 3, entonces y será 9; si x es 20, entonces y será 400.

Elija un punto A en la curva, y llame a su posición horizontal x. A continuación, elija otro punto B en la curva que esté un poco más lejos que A, y llame a su posición horizontal x + h. No importa cuánto sea h; es un número muy pequeño.

Así que cuando vamos del punto A al punto B, la posición vertical ha pasado de f(x) a f(x + h), y la posición horizontal ha pasado de x a x + h. Ahora, recuerde que la pendiente es lo que sube dividido por lo que atraviesa. Así que la pendiente será:

f ( x + h ) - f ( x ) h {\displaystyle {\frac {f(x+h)-f(x)}{h}} ${\frac {f(x+h)-f(x)}{h}}$

Si se acerca B cada vez más a A -lo que significa que h se acerca cada vez más a 0- entonces nos acercamos a saber cuál es la pendiente en el punto A.

lim h → 0 f ( x + h ) - f ( x ) h {\displaystyle \lim _{h\rightarrow 0}{{frac {f(x+h)-f(x)}{h} $\lim _{h\rightarrow 0}{\frac {f(x+h)-f(x)}{h}}$

Ahora volvamos a y = x². La pendiente de ésta se puede determinar de la siguiente manera:

= lim h → 0 f ( x + h ) - f ( x ) h = lim h → 0 ( x + h ) 2 - ( x ) 2 h {\displaystyle {\begin{aligned}&=lim _{h\rightarrow 0}{\frac {f(x+h)-f(x)}{h}\\a=lim _{h\rightarrow 0}{\frac {(x+h)^{2}-(x)^{2}}{end{aligned}} ${\begin{aligned}&=\lim _{h\rightarrow 0}{\frac {f(x+h)-f(x)}{h}}\\&=\lim _{h\rightarrow 0}{\frac {(x+h)^{2}-(x)^{2}}{h}}\end{aligned}}$

Aplicando el teorema del binomio que establece en parte que ( x + y ) 2 = x 2 + 2 x y + y 2 {\displaystyle (x+y)^{2}=x^{2}+2xy+y^{2}} $(x+y)^{2}=x^{2}+2xy+y^{2}$ , podemos reducir la expresión a

= lim h → 0 x 2 + 2 x h + h 2 - x 2 h = lim h → 0 2 x h + h 2 h = lim h → 0 2 x + h = 2 x {\displaystyle {\begin{aligned}&=lim _{h\\\\c flecha derecha 0}{\frac {x^{2}+2xh+h^{2}-x^{2}}{h}&=lim _{h\c flecha derecha 0}{\frac {2xh+h^{2}}{h}&=lim _{h\c flecha derecha 0}2x+h&={\frac {}{punto final{alineado}}. ${\begin{aligned}&=\lim _{h\rightarrow 0}{\frac {x^{2}+2xh+h^{2}-x^{2}}{h}}\\&=\lim _{h\rightarrow 0}{\frac {2xh+h^{2}}{h}}\\&=\lim _{h\rightarrow 0}2x+h\\&={\frac {}{}}2x\end{aligned}}$

Así que sabemos, sin tener que trazar ninguna línea tangente, que en cualquier punto de la curva f(x) = x², la derivada f'(x) (marcada con un apóstrofe) será 2x en cualquier punto. Este proceso de calcular una pendiente utilizando los límites se llama diferenciación, o encontrar la derivada.

Leibniz llegó al mismo resultado, pero llamó a h "dx", que significa "una pequeña cantidad de x". Llamó al cambio resultante en f(x) "dy", que significa "una pequeña cantidad de y". La notación de Leibniz se utiliza en más libros porque es fácil de entender, cuando las ecuaciones se complican. En la notación de Leibniz:

d y d x = f ′ ( x ) {\displaystyle {\frac {dy}{dx}}=f'(x)} ${\frac {dy}{dx}}=f'(x)$

Una imagen que muestra lo que significan x y x + h en la curva.

Reglas

Utilizando el sistema anterior, los matemáticos han elaborado reglas que funcionan siempre, independientemente de la función que se esté considerando. (Nota: aquí, u {\displaystyle u} $u$ y v {\displaystyle v} $v$ son ambas funciones de x {\displaystyle x} )

Condición	Función	Derivado	Ejemplo	Derivado
Un número por sí mismo	y = a {\displaystyle y=a} $y=a$	d y d x = 0 {\displaystyle {\frac {dy}{dx}}=0} ${\frac {dy}{dx}}=0$	y = 3 {\displaystyle y=3} $y=3$	0 {\displaystyle 0} $0$
Una línea recta	y = m x + c {\desde luego y=mx+c} $y=mx+c$	d y d x = m {\displaystyle {\frac {dy}{dx}}=m} ${\frac {dy}{dx}}=m$	y = 3 x + 5 {\dirección y=3x+5} $y=3x+5$	3 {\diseño de pantalla 3} $3$
x a la potencia de un número	x a {\displaystyle x^{a}} $x^{a}$	d y d x = a x a - 1 {\displaystyle {\frac {dy}{dx}}=ax^{a-1}} ${\frac {dy}{dx}}=ax^{a-1}$	x 12 {\displaystyle x^{12}} $x^{12}$	12 x 11 {\displaystyle 12x^{11}} $12x^{11}$
Un número multiplicado por una función	y = c ⋅ u {\N- y=c\cdot u} $y=c\cdot u$	d y d x = c d u d x {\displaystyle {\frac {dy}{dx}}=c{\frac {du}{dx}} ${\frac {dy}{dx}}=c{\frac {du}{dx}}$	y = 3 ( x 2 + x ) {\displaystyle y=3(x^{2}+x)} $y=3(x^{2}+x)$	3 ( 2 x + 1 ) {\dirección 3(2x+1)} $3(2x+1)$
Una función más otra función	y = u + v {\displaystyle y=u+v} $y=u+v$	d y d x = d u d x + d v d x {\frac {dy}{dx}}={frac {du}{dx}}+{\frac {dv}{dx}} ${\frac {dy}{dx}}={\frac {du}{dx}}+{\frac {dv}{dx}}$	y = 3 x 2 + x {\displaystyle y=3x^{2}+{\\c1} de la suma de los cuadrados de x}} $y=3x^{2}+{\sqrt {x}}$	6 x + 1 2 x {\displaystyle 6x+{\frac {1}{2{\frac {x}}}}} $6x+{\frac {1}{2{\sqrt {x}}}}$
Una función menos otra función	y = u - v {\displaystyle y=u-v} $y=u-v$	d y d x = d u d x - d v d x {\frac {dy}{dx}}={frac {du}{dx}}-{frac {dv}{dx}} ${\frac {dy}{dx}}={\frac {du}{dx}}-{\frac {dv}{dx}}$	y = 3 x 2 - x {\displaystyle y=3x^{2}-{\\c3}} $y=3x^{2}-{\sqrt {x}}$	6 x - 1 2 x {\displaystyle 6x-{\frac {1}{2{\frac {x}}}}} $6x-{\frac {1}{2{\sqrt {x}}}}$
Regla del producto Una función multiplicada por otra función	y = u ⋅ v {\displaystyle y=u\cdot v} $y=u\cdot v$	d y d x = d u d x v + u d v d x {\frac {dy}{dx}}={frac {du}{dx}}v+u{\frac {dv}{dx}} ${\frac {dy}{dx}}={\frac {du}{dx}}v+u{\frac {dv}{dx}}$	y = ( x 2 + x + 2 ) ( 3 x - 1 ) {\displaystyle y=(x^{2}+x+2)(3x-1)} $y=(x^{2}+x+2)(3x-1)$	( 3 x - 1 ) ( 2 x + 1 ) + 3 ( x 2 + x + 2 ) {\displaystyle (3x-1)(2x+1)+3(x^{2}+x+2)} $(3x-1)(2x+1)+3(x^{2}+x+2)$
Regla del cociente Una función dividida por otra función	y = u v {\displaystyle y={\frac {u}{v}} $y={\frac {u}{v}}$	d y d x = d u d x v - u d v d x v 2 {\displaystyle {\frac {dy}{dx}}={\frac {{du}{dx}}v-u{\frac {dv}{dx}}v^{2}}}} ${\frac {dy}{dx}}={\frac {{\frac {du}{dx}}v-u{\frac {dv}{dx}}}{v^{2}}}$	y = x 2 + 2 x - 1 {\displaystyle y={\frac {x^{2}+2}{x-1}} $y={\frac {x^{2}+2}{x-1}}$	2 x ( x - 1 ) - ( x 2 + 2 ) ( x - 1 ) 2 {\displaystyle {\frac {2x(x-1)-(x^{2}+2)}{(x-1)^{2}}}} ${\frac {2x(x-1)-(x^{2}+2)}{(x-1)^{2}}}$
Regla de la cadena Se utiliza para las funciones compuestas	y = u ∘ v {\displaystyle y=u\circ v} $y=u\circ v$	d y d x = d y d u ⋅ d u d x {\displaystyle {\frac {dy}{dx}}={frac {dy}{du}}\cdot {\frac {du}{dx}} ${\frac {dy}{dx}}={\frac {dy}{du}}\cdot {\frac {du}{dx}}$	y = 2 x - 1 {\displaystyle y={cuadrado de {2x-1}} $y={\sqrt {2x-1}}$	2 2 2 x - 1 = 1 2 x - 1 {\frac {2}{2}{sqrt {2x-1}}}}={frac {1}{sqrt {2x-1}}}} ${\frac {2}{2{\sqrt {2x-1}}}}={\frac {1}{\sqrt {2x-1}}}$
Una función exponencial	y = e x {\displaystyle {\frac {}}y=e^{x}} ${\frac {}{}}y=e^{x}$	d y d x = e x {\displaystyle {\frac {dy}{dx}}=e^{x}} ${\frac {dy}{dx}}=e^{x}$	y = e x {\displaystyle {\frac {}}y=e^{x}} ${\frac {}{}}y=e^{x}$	e x {\displaystyle {\frac {}{}e^{x}} ${\frac {}{}}e^{x}$

Páginas relacionadas

Derivada (matemáticas)
Operador diferencial
Ecuación diferencial ordinaria
Análisis matemático

Preguntas y respuestas

P: ¿Qué es el cálculo diferencial?

R: El cálculo diferencial es una rama del cálculo que estudia la tasa de cambio de una variable en comparación con otra variable, mediante el uso de funciones.

P: ¿Cómo funciona?

R: El cálculo diferencial nos permite averiguar cómo cambia una forma de un punto a otro sin necesidad de dividir la forma en un número infinito de piezas.

P: ¿Quién desarrolló el cálculo diferencial?

R: El cálculo diferencial fue desarrollado en las décadas de 1670 y 1680 por Sir Isaac Newton y Gottfried Leibniz.

P: ¿Qué es el cálculo integral?

R: El cálculo integral es lo contrario del cálculo diferencial. Se utiliza para encontrar áreas bajo curvas y volúmenes de sólidos con superficies curvas.

P: ¿Cuándo se desarrolló el cálculo diferencial?

R: El cálculo diferencial fue desarrollado en las décadas de 1670 y 1680 por Sir Isaac Newton y Gottfried Leibniz.

P: ¿Cuáles son algunas aplicaciones del cálculo diferencial?

R: Algunas aplicaciones del cálculo diferencial incluyen el cálculo de la velocidad, la aceleración, los valores máximos o mínimos, los problemas de optimización, los campos de pendiente, etc.

P: ¿Por qué utilizamos el cálculo diferencial en lugar de dividir las formas en un número infinito de piezas?

R: Utilizamos el cálculo diferencial porque nos permite averiguar cómo cambia una forma de un punto a otro sin necesidad de dividir la forma en un número infinito de piezas.