Integral de superficie: definición, cálculo y aplicaciones en física
Integral de superficie: definición clara, métodos de cálculo y aplicaciones en física (electromagnetismo). Ejemplos y ejercicios para dominar flujo y campos vectoriales.
En matemáticas, una integral de superficie es una integral definida tomada sobre una superficie (que puede ser un conjunto de curvas en el espacio). Al igual que una integral de línea maneja una dimensión o una variable, una integral de superficie puede pensarse como una doble integral a lo largo de dos dimensiones. Dada una superficie, se puede integrar sobre sus campos escalares (es decir, funciones que devuelven números como valores) y campos vectoriales (es decir, funciones que devuelven vectores como valores).
Definición y tipos
Existen principalmente dos tipos de integrales de superficie:
- Integral de superficie de un campo escalar: si σ es una superficie y φ una función escalar definida sobre σ, la integral de φ sobre σ mide, por ejemplo, la masa de una membrana si φ representa densidad superficial. Formalmente se escribe ∬_σ φ dS.
- Integral de superficie de un campo vectorial (flujo): si F es un campo vectorial definido en una vecindad de σ y n es un vector normal unitario a la superficie, la integral ∬_σ F · n dS mide el flujo del campo a través de la superficie.
Cálculo práctico
Para calcular una integral de superficie es habitual parametrizar la superficie. Sea r(u,v) una parametrización suave de σ para (u,v) en un dominio D del plano.
- Calcule los vectores parciales r_u y r_v, y su producto vectorial r_u × r_v.
- La elemento de área es dS = |r_u × r_v| dudv. Para una función escalar φ se tiene:
∬_σ φ dS = ∬_D φ(r(u,v)) · |r_u × r_v| dudv.
- Para un campo vectorial F, el flujo se obtiene como:
∬_σ F · n dS = ∬_D F(r(u,v)) · (r_u × r_v) dudv,
donde la orientación viene dada por el signo del vector r_u × r_v; si se desea el normal unitario n, entonces n = (r_u × r_v)/|r_u × r_v| y F·n dS = F·(r_u × r_v) dudv /|r_u × r_v| · |r_u × r_v| = F·(r_u × r_v) dudv.
Para superficies dadas como gráfico z = g(x,y), se usa la parametrización r(x,y) = (x, y, g(x,y)) y la diferencial de área se expresa como
dS = sqrt(1 + g_x^2 + g_y^2) dx dy,
y la normal orientada apropiadamente es ±(-g_x, -g_y, 1)/sqrt(1 + g_x^2 + g_y^2).
Condiciones y consideraciones
- La superficie debe ser suave o por partes suave para garantizar existencia de r_u y r_v y del producto vectorial.
- En superficies cerradas (como la superficie de una esfera) suele hablarse de la orientación exterior o interior; en cálculos de flujo hay que fijar una convención de orientación.
- Si la parametrización no es global, se cubre la superficie con parches parametrizados y se suman las integrales sobre cada parche, cuidando la cohesión en las fronteras.
Teoremas relacionados
- Teorema de la divergencia (de Gauss): relaciona el flujo de un campo vectorial a través de una superficie cerrada con la integral triple de la divergencia dentro del volumen encerrado.
- Teorema de Stokes: relaciona la integral de superficie del rotacional de un campo vectorial con la integral de línea del campo a lo largo de la frontera de la superficie.
Aplicaciones en física
Las integrales de superficie aparecen con frecuencia en física, y son especialmente importantes en la teoría clásica del electromagnetismo. Algunos usos relevantes:
- Ley de Gauss: el flujo del campo eléctrico a través de una superficie cerrada está relacionado con la carga eléctrica total encerrada. Esto se escribe ∬_σ E · n dS = Q_enclosed/ε0.
- Flujo magnético: la integral del campo magnético a través de una superficie (flux) aparece en la ley de Faraday y en la formulación de circuitos magnéticos.
- Transporte y conservación: en hidrodinámica y transferencia de calor, el flujo de una cantidad (masa, calor) a través de una superficie determina tasas de cambio en volúmenes.
- Masa de una lámina: si una lámina delgada tiene densidad superficial σ(x,y), su masa es ∬_σ σ dS.
Pasos prácticos para resolver un problema
- Identificar si la integral es escalar (dS) o vectorial (F·n dS).
- Elegir una parametrización r(u,v) adecuada o expresar la superficie como gráfico z = g(x,y) si conviene.
- Calcular r_u, r_v y r_u × r_v; obtener |r_u × r_v| para dS.
- Expresar la función (o el campo) en términos de (u,v), montar la integral doble sobre el dominio D y evaluar.
- Revisar la orientación si se trata de una integral de flujo y si la superficie es cerrada, considerar el signo acorde a la convención (normal exterior, por ejemplo).
Con estos elementos se puede abordar tanto el cálculo teórico como las aplicaciones físicas de las integrales de superficie, conectándolas con otras herramientas del análisis vectorial como el teorema de la divergencia y el teorema de Stokes.

La definición de integral de superficie se basa en la división de la superficie en pequeños elementos de superficie.

Una ilustración de un elemento de superficie individual. Estos elementos se hacen infinitesimalmente pequeños, por el proceso de limitación, para aproximarse a la superficie.
Integrales de superficie de campos escalares
Consideremos una superficie S sobre la que se define un campo escalar f. Si pensamos que S está hecha de algún material, y para cada x en S el número f(x) es la densidad del material en x, entonces la integral de superficie de f sobre S es la masa por unidad de espesor de S. (Esto sólo es cierto si la superficie es una cáscara infinitesimal.) Una forma de calcular la integral de superficie es dividir la superficie en muchos trozos muy pequeños, suponer que en cada trozo la densidad es aproximadamente constante, encontrar la masa por unidad de espesor de cada trozo multiplicando la densidad del trozo por su área, y luego sumar los números resultantes para encontrar la masa total por unidad de espesor de S.
Para encontrar una fórmula explícita para la integral de superficie, los matemáticos parametrizan S considerando en S un sistema de coordenadas curvilíneas, como la latitud y la longitud en una esfera. Sea dicha parametrización x(s, t), donde (s, t) varía en alguna región T del plano. Entonces, la integral de superficie viene dada por
∫ S f d S = ∬ T f ( x ( s , t ) ) | ∂ x ∂ s × ∂ x ∂ t | d s d t {\displaystyle int _{S}f,dS=\iint _{T}f(\mathbf {x} (s,t))\NIzquierda|{parcial \mathbf {x} \sobre el s parcial... a veces... sobre el t parcial... \sobre t parcial... derecho... dt...}
donde la expresión entre barras del lado derecho es la magnitud del producto cruzado de las derivadas parciales de x(s, t).
Por ejemplo, para encontrar la superficie de alguna forma funcional general, digamos z = f ( x , y ) {\displaystyle z=f\,(x,y)} , tenemos 
A = ∫ S d S = ∬ T ‖ ∂ r ∂ x × ∂ r ∂ y ‖ d x d y {\displaystyle A=\int _{S}\\️,dS=\iint _{T}\️| {{parcial \mathbf {r} \sobre x parcial... a veces... \sobre y parcial.}
donde r = ( x , y , z ) = ( x , y , f ( x , y ) ) {\displaystyle \mathbf {r} =(x,y,z)=(x,y,f(x,y))} 


A = ∬ T ‖ ( 1 , 0 , ∂ f ∂ x ) × ( 0 , 1 , ∂ f ∂ y ) ‖ d x d y = ∬ T ‖ ( - ∂ f ∂ x , - ∂ f ∂ y , 1 ) ‖ d x d y = ∬ T ( ∂ f ∂ x ) 2 + ( ∂ f ∂ y ) 2 + 1 d x d y {\displaystyle {\begin{aligned}A&{}=iint _{T} {left|||left(1,0,{\tial f \over \tial x}\right)|times |left(0,1,{\tial f \over \tial y}\right)||dx,dy\&{}=iint _{T}{left}{left}(-{parcial f sobre x},-{parcial f sobre y},1{right}){right}{dx},{dy}...{}=iint _{T} {{sqrt} {{izquierda}({parcial f |sobre |parcial x}{d})^{2}+ {{izquierda}({parcial f |sobre |parcial y}{d})^{2}+1}},|,dx,dy{final}}.
que es la fórmula utilizada para la superficie de una forma funcional general. Se puede reconocer el vector de la segunda línea anterior como el vector normal a la superficie.
Obsérvese que, debido a la presencia del producto cruzado, las fórmulas anteriores sólo funcionan para superficies incrustadas en un espacio tridimensional.
Integrales de superficie de campos vectoriales
Consideremos un campo vectorial v en S, es decir, para cada x en S, v(x) es un vector.
La integral de superficie puede definirse por componentes según la definición de la integral de superficie de un campo escalar; el resultado es un vector. Por ejemplo, esto se aplica al campo eléctrico en un punto fijo debido a una superficie cargada eléctricamente, o a la gravedad en un punto fijo debido a una lámina de material. También puede calcular el flujo magnético a través de una superficie.
Como alternativa, los matemáticos pueden integrar la componente normal del campo vectorial; el resultado es un escalar. Un ejemplo es un fluido que fluye a través de S, de manera que v(x) determina la velocidad del fluido en x. El flujo se define como la cantidad de fluido que fluye a través de S en una unidad de tiempo.
Esta ilustración implica que si el campo vectorial es tangente a S en cada punto, entonces el flujo es cero, porque el fluido sólo fluye en paralelo a S, y ni dentro ni fuera. Esto implica también que si v no fluye sólo a lo largo de S, es decir, si v tiene una componente tangencial y otra normal, entonces sólo la componente normal contribuye al flujo. Basándonos en este razonamiento, para encontrar el flujo, tenemos que tomar el producto punto de v con la normal unitaria de la superficie de S en cada punto, lo que nos dará un campo escalar, e integrar el campo obtenido como se ha dicho anteriormente. Esto da la fórmula
∫ S v ⋅ d S = ∫ S ( v ⋅ n ) d S = ∬ T v ( x ( s , t ) ) ⋅ ( ∂ x ∂ s × ∂ x ∂ t ) d s d t . {\displaystyle \int _{S} {\mathbf {v} }\cdot \\\cdot d{\mathbf {S}} }=int _{S}({\mathbf {v} }\cdot {\mathbf {n} })\iint _{T}{mathbf {v} }(\mathbf {x} (s,t))\cdot \c left({parcial \mathbf {x} \sobre s, parcial, por tiempo de {mathbf, parcial, x} \sobre t) a la derecha) ds, dt. }
El producto cruzado del lado derecho de esta expresión es una normal de superficie determinada por la parametrización.
Esta fórmula define la integral de la izquierda (nótese el punto y la notación vectorial para el elemento de la superficie).
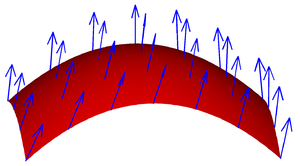
Un campo vectorial en una superficie.
Teoremas que implican integrales de superficie
Mediante la geometría diferencial y el cálculo vectorial se pueden obtener varios resultados útiles para las integrales de superficie, como el teorema de la divergencia y su generalización, el teorema de Stokes.
Cuestiones avanzadas
Modificación de la parametrización
La discusión anterior definió la integral de superficie utilizando una parametrización de la superficie S. Una superficie dada puede tener varias parametrizaciones. Por ejemplo, cuando las ubicaciones del Polo Norte y del Polo Sur se mueven en una esfera, la latitud y la longitud cambian para todos los puntos de la esfera. Una pregunta natural es entonces si la definición de la integral de superficie depende de la parametrización elegida. Para las integrales de campos escalares, la respuesta a esta pregunta es sencilla, el valor de la integral de superficie será el mismo independientemente de la parametrización que se utilice.
Las integrales de campos vectoriales son más complicadas, porque interviene la normal de la superficie. Los matemáticos han demostrado que, dadas dos parametrizaciones de la misma superficie, cuyas normales superficiales apuntan en la misma dirección, ambas parametrizaciones dan el mismo valor a la integral de superficie. Sin embargo, si las normales de estas parametrizaciones apuntan en direcciones opuestas, el valor de la integral de superficie obtenido mediante una parametrización es el negativo del obtenido mediante la otra parametrización. De ello se deduce que, dada una superficie, no necesitamos ceñirnos a ninguna parametrización única; pero, al integrar campos vectoriales, sí necesitamos decidir de antemano hacia qué dirección apuntará la normal y, a continuación, elegir cualquier parametrización coherente con esa dirección.
Las parametrizaciones funcionan en partes de la superficie
Otro problema es que a veces las superficies no tienen parametrizaciones que cubran toda la superficie; es el caso, por ejemplo, de la superficie de un cilindro (de altura finita). La solución obvia es dividir esa superficie en varios trozos, calcular la integral de superficie en cada trozo y luego sumarlos todos. De hecho, así es como funcionan las cosas, pero al integrar campos vectoriales hay que volver a tener cuidado con la elección del vector de punto normal para cada trozo de la superficie, de modo que cuando se vuelvan a juntar los trozos, los resultados sean coherentes. Para el cilindro, esto significa que si decidimos que para la región lateral la normal apuntará fuera del cuerpo, entonces para las partes circulares superior e inferior la normal debe apuntar también fuera del cuerpo.
Normales de superficie incoherentes
Por último, hay superficies que no tienen una normal de superficie en cada punto con resultados coherentes (por ejemplo, la banda de Möbius). Si una superficie de este tipo se divide en trozos, en cada trozo se elige una parametrización y la correspondiente normal de superficie, y se vuelven a juntar los trozos, los vectores normales procedentes de los distintos trozos no pueden conciliarse. Esto significa que en alguna unión entre dos piezas habrá vectores normales que apunten en direcciones opuestas. Una superficie así se denomina no orientable. Los campos vectoriales no pueden integrarse en superficies no orientables.
Páginas relacionadas
- Teorema de la divergencia
- Teorema de Stokes
- Línea integral
- Volumen integral
- Sistema de coordenadas cartesianas
- Elementos de volumen y superficie en un sistema de coordenadas esféricas
- Elementos de volumen y superficie en un sistema de coordenadas cilíndricas
- Método Holstein-Herring
Buscar dentro de la enciclopedia



