Leyes de Kepler: definición y explicación del movimiento planetario

Descubre las 3 Leyes de Kepler: explicación clara del movimiento planetario, órbitas elípticas, áreas iguales y relación periodo‑semieje mayor con ejemplos prácticos.

Autor: Leandro Alegsa

Las leyes de Kepler del movimiento planetario son tres leyes que describen el movimiento de los planetas alrededor del sol:

  1. Los planetas se mueven alrededor del sol en órbitas elípticas. El sol se encuentra en uno de los dos focos de la órbita.
  2. Un segmento de línea que une un planeta y el Sol barre áreas iguales durante intervalos de tiempo iguales.
  3. El cuadrado del periodo orbital de un planeta es proporcional al cubo del semieje mayor de su órbita.

Johannes Kepler encontró estas leyes, entre 1609 y 1619.

Contexto histórico breve

Kepler formuló estas leyes utilizando las detalladas observaciones de Tycho Brahe. Publicó las dos primeras leyes en 1609 en la obra Astronomia Nova y la tercera en 1619 en Harmonices Mundi. Más tarde, Isaac Newton mostró que las leyes de Kepler son consecuencia de la ley de la gravitación universal y las leyes del movimiento, integrando así la dinámica y la geometría del movimiento planetario.

Explicación y significado de cada ley

Primera ley: órbitas elípticas

Enunciado: Cada planeta se desplaza en una órbita elíptica con el Sol en uno de sus focos.

Esto significa que la distancia entre el planeta y el Sol varía a lo largo de la órbita. Los puntos más cercanos y más lejanos se llaman perihelio y afelio, respectivamente. La forma de la elipse se caracteriza por su excentricidad e (0 ≤ e < 1): cuanto más próxima a 0, más circular es la órbita. Por ejemplo, la Tierra tiene una excentricidad baja (~0,0167), por eso su órbita es casi circular.

Segunda ley: áreas iguales (velocidad areolar constante)

Enunciado: El segmento que une el planeta y el Sol barre áreas iguales en tiempos iguales.

En términos físicos esto implica que la velocidad areolar (dA/dt) es constante, lo que es equivalente a la conservación del momento angular en el movimiento central. Consecuencia práctica: un planeta se mueve más rápido cuando está más cerca del Sol (perihelio) y más lento cuando está más lejos (afelio).

Tercera ley: relación entre periodo y semieje mayor

Enunciado: El cuadrado del periodo orbital (T) de un planeta es proporcional al cubo del semieje mayor (a) de su órbita: T² ∝ a³.

Para el caso de un cuerpo pequeño orbitando un cuerpo central mucho más masivo (problema de dos cuerpos), la constante de proporcionalidad se puede escribir explícitamente usando la constante gravitatoria G y la masa del cuerpo central M:

T² = (4π² / GM) · a³

En el Sistema Solar, si T se expresa en años y a en unidades astronómicas (AU), la constante se aproxima a 1 para objetos alrededor del Sol, por eso suele decirse que T² = a³ (en esas unidades). Esta relación permite, por ejemplo, estimar la masa de la estrella central midiendo periodos y tamaños de órbita de sus planetas o satélites.

Aplicaciones y limitaciones

  • Aplicaciones: cálculo de órbitas de planetas y satélites, diseño de trayectorias espaciales, estimación de masas estelares, estudio de sistemas exoplanetarios y enseñanza básica de mecánica orbital.
  • Limitaciones: Las leyes de Kepler son exactas para el problema de dos cuerpos bajo la gravitación newtoniana. En sistemas con múltiples cuerpos (efectos de perturbación), con cuerpos de masas comparables, o cuando se requieren correcciones relativistas (p. ej. el avance del perihelio de Mercurio), hay desviaciones que exigen tratamientos más complejos.

Notas adicionales

Las leyes de Kepler supusieron un cambio importante respecto a los modelos anteriores (como las órbitas circulares y epiciclos). Su interpretación moderna se relaciona con conceptos de conservación (energía, momento angular) y con la ley de gravitación de Newton, que proporciona el fundamento físico de por qué las trayectorias son elipses y por qué se cumple la tercera ley en la forma indicada.

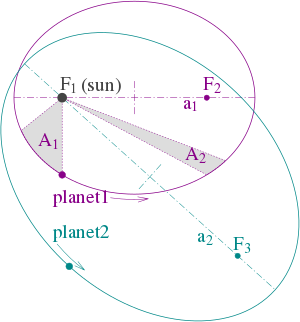
Figura 1: Ilustración de las tres leyes de Kepler con dos órbitas planetarias. (1) Las órbitas son elipses, con focos ƒ 1y ƒ 2para el primer planeta y ƒ 1y ƒ 3para el segundo. El Sol se sitúa en el punto focal ƒ 1. (2) Los dos sectores sombreados A1 y A2 tienen la misma superficie y el tiempo para que el planeta 1 cubra el segmento A 1es igual al tiempo para cubrir el segmento A 2. (3) Los tiempos orbitales totales del planeta 1 y del planeta 2 tienen una relación a 13/2: a 23/2.Zoom
Figura 1: Ilustración de las tres leyes de Kepler con dos órbitas planetarias. (1) Las órbitas son elipses, con focos ƒ 1y ƒ 2para el primer planeta y ƒ 1y ƒ 3para el segundo. El Sol se sitúa en el punto focal ƒ 1. (2) Los dos sectores sombreados A1 y A2 tienen la misma superficie y el tiempo para que el planeta 1 cubra el segmento A 1es igual al tiempo para cubrir el segmento A 2. (3) Los tiempos orbitales totales del planeta 1 y del planeta 2 tienen una relación a 13/2: a 23/2.

Comparación con Copérnico

Las leyes de Kepler mejoran el modelo de Copérnico. Si las excentricidades de las órbitas planetarias se toman como cero, entonces Kepler está básicamente de acuerdo con Copérnico:

  1. La órbita planetaria es un círculo
  2. El Sol en el centro de la órbita
  3. La velocidad del planeta en la órbita es constante

Las excentricidades de las órbitas de los planetas conocidos por Copérnico y Kepler son pequeñas, por lo que las reglas anteriores dan buenas aproximaciones al movimiento planetario; pero las leyes de Kepler se ajustan mejor a las observaciones que las de Copérnico.

Las correcciones de Kepler no son en absoluto evidentes:

  1. La órbita planetaria no es un círculo, sino una elipse.
  2. El Sol no está en el centro sino en un punto focal de la órbita elíptica.
  3. Ni la velocidad lineal ni la angular del planeta en la órbita son constantes, pero la velocidad de área sí lo es.

La excentricidad de la órbita de la Tierra hace que el tiempo desde el equinoccio de marzo hasta el equinoccio de septiembre, unos 186 días, sea desigual al tiempo desde el equinoccio de septiembre hasta el equinoccio de marzo, unos 179 días. Un diámetro cortaría la órbita en partes iguales, pero el plano que pasa por el sol paralelo al ecuador de la tierra corta la órbita en dos partes con áreas en una proporción de 186 a 179, por lo que la excentricidad de la órbita de la tierra es aproximadamente

ε ≈ π 4 186 - 179 186 + 179 ≈ 0,015 , {\displaystyle \varepsilon \approx {\frac {\pi }{4}}{\frac {186-179}{186+179}}approx 0,015,} {\displaystyle \varepsilon \approx {\frac {\pi }{4}}{\frac {186-179}{186+179}}\approx 0.015,}

que se acerca al valor correcto (0,016710219) (véase la órbita de la Tierra). El cálculo es correcto cuando el perihelio, la fecha en que la Tierra está más cerca del Sol, cae en un solsticio. El perihelio actual, cercano al 4 de enero, está bastante cerca del solsticio del 21 de diciembre



Buscar dentro de la enciclopedia
AlegsaOnline.com - 2020 / 2025 - License CC3