Círculo de quintas
En teoría musical, el círculo de quintas muestra cómo se relacionan las diferentes tonalidades entre sí. Suele mostrarse como un círculo con los nombres de las tonalidades a su alrededor. Si tomas cualquier tecla del círculo, su quinta es la que está a su derecha. Se puede entender fácilmente junto con un teclado de piano.
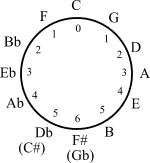
La disposición de un teclado musical típico traducido a un círculo de quintas
Estructura
En un piano hay notas blancas y negras (confusamente también se llaman "teclas"). Las notas blancas se denominan con las letras A a G del alfabeto. Después de la G viene otra A y así sucesivamente. Las notas negras van de tres en tres. Esto hace que sea fácil ver el patrón de las notas blancas. Cuando hay dos notas negras juntas, por ejemplo, la nota blanca entre ellas es Re. Las notas negras no tienen nombre propio. Reciben el nombre de las notas blancas que están a su lado. La nota negra situada justo encima (es decir, a la derecha) de un sol es un sol sostenido. La nota negra situada justo debajo (es decir, a la izquierda) de un sol es un sol bemol. Esto significa que cada nota negra tiene dos nombres posibles (por ejemplo, sol bemol o fa sostenido).
Método
Al tocar cada nota, ya sea una blanca o una negra, se obtiene una escala cromática (por ejemplo, Do, Do sostenido, Re, Mi bemol, Mi, Fa, Fa sostenido, Sol, La bemol, La, Si bemol, Si, Do). Cada paso se denomina "semitono" o "semitono". Por tanto, un "tono" o "tono entero" es un salto de dos semitonos (de Do a Re, o de Do sostenido a Mi bemol, o de Mi a Fa sostenido).
Tocando en las notas blancas de Do a la siguiente Do obtenemos una escala mayor. Algunos de los pasos son tonos y otros son semitonos. Los semitonos se encuentran entre Mi y Fa y entre Si y Do, es decir, entre la 3ª y la 4ª y entre la 7ª y la 8ª nota de la escala. Todas las escalas mayores tienen este patrón (tono, tono, semitono, tono, tono, semitono).
Ejemplos
- Empezar una escala en un sol significa que el fa tiene que ser un fa sostenido. Este fa sostenido, la 7ª nota de la escala, se escribe en la armadura cuando se escribe una pieza en clave de sol mayor.
- Empezar una escala en un re significa que el fa y el do tienen que ser fa sostenido y do sostenido.
- Empezar una escala en un La significa que el Fa, el Do y el Sol tienen que ser sostenidos.
- Podemos continuar así hasta que las siete notas sean sostenidas (Do sostenido mayor).
Cada vez que pasamos a una tonalidad más aguda, tomamos la nota que era la 5ª nota de la escala anterior (Sol, con un sostenido, era la 5ª nota de Do mayor. Re, con dos sostenidos, era la 5ª nota de Sol, etc.).
En un diagrama, esto puede representarse como un círculo que se denomina "Círculo de Quintas". A medida que nos vamos afinando, vamos dando vueltas al círculo en el sentido de las agujas del reloj.
Pisos
Los bemoles funcionan exactamente al revés. En lugar de subir a la quinta nota (por ejemplo, Do, Re, Mi, Fa, Sol) podemos bajar una quinta (Do, Si, La, Sol, Fa). El fa es la escala que tiene un bemol. A medida que vayamos bajando el bemol, iremos dando vueltas al círculo en sentido contrario a las agujas del reloj hasta que las siete notas estén bemoles.
Se puede ver que tres de las escalas tienen dos nombres posibles cada una: Si mayor (con 5 sostenidos) también puede considerarse como Do bemol mayor (con siete bemoles), Fa sostenido mayor (con 6 sostenidos) también puede considerarse como Sol bemol mayor (con 6 bemoles), y Do sostenido mayor (con 7 sostenidos) también puede considerarse como Re bemol mayor (con 5 bemoles).
Menores
Los menores relativos (la escala menor con la misma armadura) también se pueden calcular dando tres pasos en el círculo (Do mayor es el mayor relativo de La menor, es decir, comparte la misma armadura: nada). En un teclado, el relativo menor puede calcularse bajando tres semitonos (de Do se baja a Si, Si bemol, La).
| ||||||||
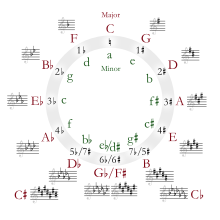
Una versión más compleja del círculo de quintas que incluye las menores.
Preguntas y respuestas
P: ¿Qué es el círculo de quintas en teoría musical?
R: El círculo de quintas es una herramienta de la teoría musical que muestra cómo se relacionan entre sí las diferentes tonalidades.
P: ¿Cómo se suele representar el círculo de quintas?
R: El círculo de quintas suele representarse como un círculo con los nombres de las tonalidades a su alrededor.
P: ¿Cuál es la relación entre las claves del círculo de quintas?
R: Las claves del Círculo de quintas están relacionadas entre sí por su distancia de una quinta.
P: ¿Qué es una quinta en teoría musical?
R: En teoría musical, una quinta se refiere a la distancia entre dos notas musicales que están a cinco notas de distancia una de otra.
P: ¿Cuál es la relación entre cualquier tonalidad del Círculo de quintas y la tonalidad situada a su derecha?
R: La quinta de cualquier tonalidad del Círculo de quintas es la tonalidad situada a su derecha.
P: ¿Cómo se puede entender fácilmente el Círculo de quintas junto con un teclado de piano?
R: El círculo de quintas se puede entender fácilmente con el teclado de un piano siguiendo la secuencia de las teclas que están a una quinta de distancia.
P: ¿Qué importancia tiene el círculo de quintas en la teoría musical?
R: El círculo de quintas es importante en la teoría musical porque ayuda a los músicos a comprender las relaciones entre las diferentes tonalidades y les permite utilizar este conocimiento para componer música.
Buscar dentro de la enciclopedia