Ley de Ampère

Ley circuital original de Ampère

La ley relaciona los campos magnéticos con las corrientes eléctricas que los producen. Un científico puede utilizar la ley de Ampère para determinar el campo magnético asociado a una corriente dada o la corriente asociada a un campo magnético dado, si no hay un campo eléctrico que cambie en el tiempo. En su forma original, la Ley Circuital de Ampère relaciona el campo magnético con su fuente de corriente eléctrica. La ley puede escribirse de dos formas, la "forma integral" y la "forma diferencial". Las formas son equivalentes y están relacionadas por el teorema de Kelvin-Stokes. También puede escribirse en términos de los campos magnéticos B o H. Una vez más, las dos formas son equivalentes (véase la sección de "pruebas" más adelante).

Ahora se sabe que la ley circuital de Ampère es una ley física correcta en una situación magnetostática: El sistema es estático, excepto, posiblemente, en el caso de corrientes continuas estables dentro de bucles cerrados. En todos los demás casos, la ley es incorrecta a menos que se incluya la corrección de Maxwell (véase más adelante).

Forma integral

En unidades del SI (la versión en unidades cgs está en una sección posterior), la "forma integral" de la ley circuital original de Ampère es:

• ∮ C B ⋅ d ℓ = μ 0 ∬ S J ⋅ d S {\displaystyle \oint _{C}\mathbf {B}} \Punto de la matriz d, símbolo de negrita, = punto de la matriz S, punto de la matriz J. \...y el símbolo de la letra de oro... \{{0}} {{0} {{0}} iint _{S}} }
• ∮ C H ⋅ d ℓ = ∬ S J f ⋅ d S {\displaystyle \oint _{C}{mathbf {H}} \Punto de la matriz d, símbolo en negrita, = punto de la matriz J. ...que se encuentra en el centro de la ciudad. {{cdot}} {{mathrm}} {{d}} \{{mathbf}} {{S}} }

o de forma equivalente,

• ∮ C B ⋅ d ℓ = μ 0 I e n c {\displaystyle \oint _{C}\mathbf {B}} \cdot \mathrm {d} {\boldsymbol {\ell }}=\mu _{0}I_{\mathrm {enc}} }}
• ∮ C H ⋅ d ℓ = I f , e n c {\displaystyle \oint _{C} {mathbf {H}} \{\cdot} {\cathrm {d} {\boldsymbol }}=I_{\mathrm {f,enc}} }}

donde

• - es el producto punto vectorial, ∮ C {\displaystyle \textstyle \oint _{C}} es la integral de línea cerrada alrededor de la curva cerrada C, ∬ S {\displaystyle \textstyle \iint _{S}} denota una integral sobre la superficie S encerrada por la curva C (el signo de doble integral se entiende simplemente para denotar que la integral es de naturaleza bidimensional);
• B es el campo magnético B en teslas, H es el campo magnético H en amperios por metro;
• I_f,enc es la corriente libre neta que penetra a través de la superficie S, I_enc es la corriente neta total que penetra a través de la superficie S, incluyendo tanto la corriente libre como la ligada.
• J_f es la densidad de corriente libre a través de la superficie S delimitada por la curva C, J es la densidad de corriente total a través de la superficie S delimitada por la curva C, incluyendo tanto la corriente libre como la corriente ligada;
• dℓ es un elemento infinitesimal (una diferencial) de la curva C (es decir, un vector con magnitud igual a la longitud del elemento lineal infinitesimal, y dirección dada por la tangente a la curva C), dS es el vector área de un elemento infinitesimal de la superficie S (es decir, un vector con magnitud igual al área del elemento superficial infinitesimal, y dirección normal a la superficie S. La dirección de la normal debe corresponder con la orientación de C por la regla de la mano derecha);
• μ₀ es la constante magnética;

Más adelante se explican mejor la curva C y la superficie S. Hay una serie de ambigüedades en las definiciones anteriores que requieren una aclaración y una elección de la convención.

En primer lugar, tres de estos términos están asociados con ambigüedades de signo: la integral de línea ∮ C {\displaystyle \textstyle \oint _{C}} podría ir alrededor del bucle en cualquier dirección (en el sentido de las agujas del reloj o en sentido contrario); el área vectorial dS podría apuntar en cualquiera de las dos direcciones normales a la superficie; y I_enc es la corriente neta que pasa a través de la superficie S, lo que significa la corriente que pasa en una dirección, menos la corriente en la otra dirección-pero cualquier dirección podría ser elegida como positiva. Estas ambigüedades se resuelven con la regla de la mano derecha: Con la palma de la mano derecha hacia el área de integración, y el dedo índice apuntando a lo largo de la dirección de integración de la línea, el pulgar extendido apunta en la dirección que debe ser elegida para el área vectorial dS. También la corriente que pasa en la misma dirección que dS debe contarse como positiva. La regla de la mano derecha también se puede utilizar para determinar los signos.

En segundo lugar, existen infinitas superficies posibles S que tienen como frontera la curva C. (Imagina una película de jabón sobre un bucle de alambre, que puede deformarse moviendo el alambre). ¿Cuál de esas superficies hay que elegir? Si el bucle no está en un solo plano, por ejemplo, no hay una opción obvia. La respuesta es que no importa; se puede demostrar que se puede elegir cualquier superficie con límite C.

Forma diferencial

Por el teorema de Kelvin-Stokes, esta ecuación también puede escribirse en "forma diferencial". De nuevo, esta ecuación sólo se aplica en el caso de que el campo eléctrico sea constante en el tiempo; véase más adelante la forma más general. En unidades del SI, la ecuación dice

∇ × B = μ 0 J {\displaystyle \mathbf {\nabla } \N - veces \mathbf {B} =\mu _{0}\mathbf {J} }

∇ × H = J f {\displaystyle \mathbf {\nabla } \N - veces \Nmathbf {H} =\Nmathbf {J_{f}} }

donde

∇ × {\displaystyle \mathbf {\nabla } \ es el operador de rizo.  

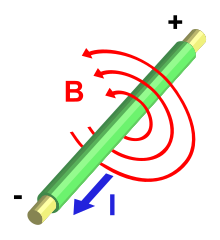
Una corriente eléctrica produce un campo magnético.  

Nota sobre la corriente libre frente a la corriente ligada

La corriente eléctrica que surge en las situaciones más sencillas del libro de texto se clasificaría como "corriente libre". Por ejemplo, la ley puede aplicarse a la corriente que pasa por un cable o una batería. En cambio, la "corriente ligada" surge en el contexto de los materiales a granel que pueden ser magnetizados y/o polarizados. (Todos los materiales pueden hacerlo en cierta medida).

Cuando se magnetiza un material (por ejemplo, colocándolo en un campo magnético externo), los electrones permanecen ligados a sus respectivos átomos, pero se comportan como si orbitaran alrededor del núcleo en una dirección determinada, creando una corriente microscópica. Cuando las corrientes de todos estos átomos se juntan, crean el mismo efecto que una corriente macroscópica, circulando perpetuamente alrededor del objeto magnetizado. Esta corriente de magnetización J_M es una contribución a la "corriente ligada".

La otra fuente de corriente ligada es la carga ligada. Cuando se aplica un campo eléctrico, las cargas ligadas positivas y negativas pueden separarse a lo largo de las distancias atómicas en los materiales polarizables, y cuando las cargas ligadas se mueven, la polarización cambia, creando otra contribución a la "corriente ligada", la corriente de polarización J_P .

La densidad de corriente total J debida a las cargas libres y ligadas es entonces:

J = J f + J M + J P , {\displaystyle \mathbf {J} =\mathbf {J_{f}+J_{M}+J_{P}} \ ,}

con J_f la densidad de corriente "libre" o "de conducción".

Todas las corrientes son fundamentalmente iguales, desde el punto de vista microscópico. A menudo hay razones prácticas para querer tratar la corriente ligada de forma diferente a la corriente libre. Por ejemplo, la corriente ligada suele originarse en dimensiones atómicas, y se puede querer aprovechar una teoría más sencilla pensada para dimensiones mayores. El resultado es que la ley de Ampère, más microscópica, expresada en términos de B y de la corriente microscópica (que incluye las corrientes libres, de magnetización y de polarización), se pone a veces en la forma equivalente que se presenta a continuación en términos de H y de la corriente libre solamente. Para una definición detallada de la corriente libre y la corriente ligada, y la prueba de que las dos formulaciones son equivalentes, véase la sección "prueba" más abajo.

 

Deficiencias de la formulación original de la ley circuital de Ampère

Hay dos cuestiones importantes relacionadas con la ley de Ampère. En primer lugar, hay una cuestión relacionada con la ecuación de continuidad de la carga eléctrica. Hay un teorema en el cálculo vectorial que establece que la divergencia de un rizo debe ser siempre cero. Por lo tanto,

∇ ⋅ ( ∇ × B ) = 0 {\displaystyle \nabla \cdot (\nabla \times {\mathbf {B})=0}

por lo que la ley de Ampère original implica que

∇ ⋅ J = 0 {\displaystyle \nabla \cdot {\mathbf {J}}=0}

Pero en general

∇ ⋅ J = - ∂ ρ ∂ t {\displaystyle \nabla \cdot {\mathbf {J}}=-{\frac {\partial \rho }{\partial t}}

que es distinto de cero para una densidad de carga variable en el tiempo. Un ejemplo se da en un circuito de condensadores donde existen densidades de carga variables en el tiempo en las placas.

En segundo lugar, existe un problema relacionado con la propagación de las ondas electromagnéticas. Por ejemplo, en el espacio libre, donde

J = 0 {\displaystyle {\mathbf {J}}={mathbf {0}}

La ley de Ampère implica que

∇ × B = 0 {\displaystyle \nabla \\N veces {\mathbf {B}}={mathbf {0}}

pero en cambio

∇ × B = - 1 c 2 ∂ E ∂ t {{displaystyle \nabla \\\\Nmathbf {B}}=-{\frac {1}{c^{2}} {{frac {\mathbf {E}} {{parcial t}}

Para tratar estas situaciones, la contribución de la corriente de desplazamiento debe añadirse al término de corriente en la ley de Ampère.

James Clerk Maxwell concibió la corriente de desplazamiento como una corriente de polarización en el mar de vórtices dieléctricos, que utilizó para modelar el campo magnético con agua (hidrodinámicamente) y con sistemas mecánicos (mecánicamente). Añadió esta corriente de desplazamiento a la ley circuital de Ampère en la ecuación (112) en su artículo de 1861 On Physical Lines of Force .

Corriente de desplazamiento

En el espacio libre, la corriente de desplazamiento está relacionada con la tasa de cambio temporal del campo eléctrico.

En un dieléctrico, la contribución anterior a la corriente de desplazamiento también está presente, pero una contribución mayor a la corriente de desplazamiento está relacionada con la polarización de las moléculas individuales del material dieléctrico. Aunque las cargas no pueden fluir libremente en un dieléctrico, las cargas de las moléculas pueden moverse un poco bajo la influencia de un campo eléctrico. Las cargas positivas y negativas de las moléculas se separan bajo el campo aplicado, provocando un aumento del estado de polarización, expresado como densidad de polarización P. Un estado de polarización cambiante equivale a una corriente.

Ambas contribuciones a la corriente de desplazamiento se combinan definiendo la corriente de desplazamiento como

J D = ∂ ∂ t D ( r , t ) , {\displaystyle \mathbf {J_{D}} = {\frac {\partial }{partial t}} ({\boldsymbol {r}},\ t)\} ,}

donde el campo de desplazamiento eléctrico se define como

D = ε 0 E + P = ε 0 ε r E , {\displaystyle \mathbf {D} =\varepsilon _{0}\mathbf {E} +\mathbf {P} =\varepsilon _{0}\varepsilon _{r}\mathbf {E} \ ,}

donde ε₀ es la constante eléctrica, ε_r la permitividad estática relativa, y P es la densidad de polarización. Sustituyendo esta forma de D en la expresión de la corriente de desplazamiento, ésta tiene dos componentes:

J D = ε 0 ∂ E ∂ t + ∂ P ∂ t . {\displaystyle \mathbf {J} {{mathrm {D}} {\i1}Varepsilon _{0}{{\i} {\i}parcial \i} {\i}E}{\i} {\i}parcial t}{\i}. {{parcial t}}+{{frac}{parcial \mathbf {P}} {{parcial t}} {{parcial t}}. }

El primer término de la derecha está presente en todas partes, incluso en el vacío. No implica ningún movimiento real de carga, pero sin embargo tiene un campo magnético asociado, como si fuera una corriente real. Algunos autores aplican el nombre de corriente de desplazamiento sólo a esta contribución.

El segundo término del lado derecho es la corriente de desplazamiento, tal como la concibió originalmente Maxwell, asociada a la polarización de las moléculas individuales del material dieléctrico.

La explicación original de Maxwell sobre la corriente de desplazamiento se centraba en la situación que se produce en los medios dieléctricos. En la era moderna posterior al éter, el concepto se ha ampliado para aplicarlo a situaciones sin medios materiales presentes, por ejemplo, al vacío entre las placas de un condensador de vacío que se carga. La corriente de desplazamiento se justifica hoy en día porque cumple varios requisitos de una teoría electromagnética: predicción correcta de los campos magnéticos en regiones donde no fluye la corriente libre; predicción de la propagación de ondas de los campos electromagnéticos; y conservación de la carga eléctrica en casos en los que la densidad de carga varía en el tiempo. Para una mayor discusión, véase Corriente de desplazamiento.

 

Ampliación de la ley original: la ecuación de Maxwell-Ampère

La ecuación de Ampère se amplió incluyendo la corriente de polarización, con lo que se subsanó la limitada aplicabilidad de la ley circuital de Ampère original.

Tratando las cargas libres por separado de las cargas ligadas, la ecuación de Ampère incluyendo la corrección de Maxwell en términos del campo H es (se utiliza el campo H porque incluye las corrientes de magnetización, por lo que J_M no aparece explícitamente, ver campo H y también Nota):

∮ C H ⋅ d ℓ = ∬ S ( J f + ∂ t D ) ⋅ d A {\displaystyle \oint _{C}\mathbf {H}} \Punto de la matriz d = punto de la matriz J = punto de la matriz J = punto de la matriz J ...y el símbolo de la letra en negrita... {{frac}} {{parcial}} {{parcial t}} {{mathbf}} {{D}} \cdot \mathrm {d} \...de la que se trata. }

(forma integral), donde H es el campo magnético H (también llamado "campo magnético auxiliar", "intensidad del campo magnético", o simplemente "campo magnético", D es el campo de desplazamiento eléctrico, y J_f es la corriente de conducción encerrada o la densidad de corriente libre. En forma diferencial,

∇ × H = J f + ∂ ∂ t D . {\displaystyle \mathbf {\nabla } \N - veces \Nmathbf {H} =\Nmathbf {J} {{mathrm {f}} {\frac {\parcial} {\parcial t} = {mathbf {D} \ . }

Por otro lado, tratando todas las cargas en igualdad de condiciones (sin tener en cuenta si son cargas ligadas o libres), la ecuación de Ampère generalizada (también llamada ecuación de Maxwell-Ampère) es (véase la sección "prueba" más adelante):

∮ C B ⋅ d ℓ = ∬ S ( μ 0 J + μ 0 ϵ 0 ∂ ∂ t E ) ⋅ d A {\displaystyle \oint _{C}\mathbf {B}} \{\cdot} {\mathrm {d} {\boldsymbol {\ell }}=\iint _{S} {\i1}Izquierda(\mu _{0} {mathbf {J} + epsilon _{0} {{frac} {{parcial}} {{parcial t}}. \(derecha)\N-dota \Nmathrm {d} \...de la que se trata. }

en forma integral. En forma diferencial,

∇ × B = ( μ 0 J + μ 0 ϵ 0 ∂ ∂ t E ) . {\displaystyle \mathbf {\nabla } \N - veces \N - B = (\N - 0 - J) + +epsilon _{0} {{frac} {{parcial}} {{parcial t}} {{mathbf {E}} )\ . }

En ambas formas, J incluye la densidad de corriente de magnetización, así como las densidades de corriente de conducción y polarización. Es decir, la densidad de corriente en el lado derecho de la ecuación de Ampère-Maxwell es:

J f + J D + J M = J f + J P + J M + ε 0 ∂ E ∂ t = J + ε 0 ∂ E ∂ t , {\displaystyle \mathbf {J_{f}+J_{D}+J_{M}} =\mathbf {J_{f}+J_{P}+J_{M}} +\varepsilon _{0}{frac {\parcial \mathbf} =\mathbf {{P}+J_{M}}. +\varepsilon _{0} {\frac {parcial \mathbf {E}} {{parcial t}}={mathbf {J}} +varepsilon _{0} {{frac} {{parcial} {E} {{parcial}} ...t...

donde la densidad de corriente J_D es la corriente de desplazamiento, y J es la contribución de la densidad de corriente debida realmente al movimiento de las cargas, tanto libres como ligadas. Debido a que ∇ - D = ρ, el problema de continuidad de carga con la formulación original de Ampère ya no es un problema. Debido al término en ε₀ ∂E / ∂t, la propagación de la onda en el espacio libre ahora es posible.

Con la adición de la corriente de desplazamiento, Maxwell pudo hipotetizar (correctamente) que la luz era una forma de onda electromagnética. Véase la ecuación de la onda electromagnética para una discusión de este importante descubrimiento.

Prueba de equivalencia

Prueba de que las formulaciones de la ley de Ampère en términos de corriente libre son equivalentes a las formulaciones que implican la corriente total.

En esta prueba, mostraremos que la ecuación ∇ × H = J f + ∂ D ∂ t {\displaystyle \nabla \mathbf {H} =\mathbf {J} { {{favorable}) _{f}+{{frac} {{parcial} {D} }{mathbf}} {{parcial t}} es equivalente a la ecuación ∇ × B / μ 0 = J + ϵ 0 ∂ E ∂ t {\displaystyle \mathbf {\nabla } \N - tiempos \N - B /\mu _{0}=\mathbf {J} +epsilon _{0} {\frac {\parcial \mathbf {E}} {{parcial t}} Nótese que sólo estamos tratando con las formas diferenciales, no con las integrales, pero eso es suficiente ya que las formas diferenciales e integrales son equivalentes en cada caso, por el teorema de Kelvin-Stokes. Introducimos la densidad de polarización P, que tiene la siguiente relación con E y D: D = ϵ 0 E + P {\displaystyle \mathbf {D} =epsilon _{0}\mathbf {E} +\Nmathbf {P} } A continuación, introducimos la densidad de magnetización M, que tiene la siguiente relación con B y H: B / μ 0 = H + M {\displaystyle \mathbf {B} /\mu _{0}=\mathbf {H} +\mathbf {M} } y la siguiente relación con la corriente límite: J b o u n d = ∇ × M + ∂ P ∂ t , {\displaystyle \mathbf {J} _{mathrm {bound} }=\nabla \mathbf {M}. {{mathrm {bound} }={nabla \\\\N}mathbf {M} +{{frac}} {{parcial}} {{P}} {{parcial t}} ,} = J M + J P , {\displaystyle =\mathbf {J} {{mathrm {M}} {{mathbf}} + {{mathbf}} J J M + J P, estilo de visualización =mathbf {J} _{mathrm {M} }+mathbf {J} }\ ,} donde J M = ∇ × M , {\displaystyle \mathbf {J} {{mathrm {M}} = {\nabla \\}} {\nabla \\\\\Nde las veces que se ha hecho el mathbf {M} \ ,} se denomina densidad de corriente de magnetización, y J P = ∂ P ∂ t , {{displaystyle \mathbf {J}} {{mathrm {P}} }={fracción {{parcial \mathbf {P}} {{parcial t}} {{parcial t}} ,} es la densidad de corriente de polarización. Tomando la ecuación de B: ∇ × B / μ 0 = ∇ × ( H + M ) {\displaystyle \mathbf {\nabla } \N - veces \Nmathbf {B} /\mu _{0}=\mathbf {\nabla } \(H+M) a la derecha) = ∇ × H + J M {\displaystyle =\mathbf {\nabla } \N - veces \N que el H se convierte en un elemento de la vida cotidiana. +\Nmathbf {J_{M}} } = J f + J P + ε 0 ∂ E ∂ t + J M {\displaystyle =\mathbf {J_{f}} +\mathbf {J_{P}} +\mathbf {J_{P}} +\varepsilon _{0} {\frac {\parcial \mathbf {E}} {{parcial t}}+{mathbf {J_{M}} } Por lo tanto, refiriéndonos a la definición de la corriente limitada: ∇ × B / μ 0 = J f + J b o u n d + ε 0 ∂ E ∂ t {\displaystyle \mathbf {\nabla } \N - tiempos \N de la B. /\mu _{0}=\mathbf {J_{f}} +\mathbf {J} + varepsilon _{0} {{frac} {{parcial} {E}} {{parcial t}} = J + ε 0 ∂ E ∂ t , {\displaystyle =\mathbf {J} +\farepsilon _{0} {\frac {\partial \mathbf {E} +\varepsilon _{0} {\frac {\parcial \mathbf {E}} t}} ,} como se iba a demostrar.

 

Ley de Ampère en unidades cgs

En unidades cgs, la forma integral de la ecuación, incluyendo la corrección de Maxwell, dice

∮ C B ⋅ d ℓ = 1 c ∬ S ( 4 π J + ∂ E ∂ t ) ⋅ d S {\displaystyle \oint _{C}{mathbf {B}} \cdot \mathrm {d} {\boldsymbol {\ell }}= {\frac {1}{c}\iint _{S}}left(4\pi \mathbf {J} +{\frac \mathbf {E}{partial t}}right)\cdot \mathrm {d} \...de la que se desprende el nombre de la empresa. }

donde c es la velocidad de la luz.

La forma diferencial de la ecuación (de nuevo, incluyendo la corrección de Maxwell) es

∇ × B = 1 c ( 4 π J + ∂ E ∂ t ) .  \N - B = {\frac {1}{c}}left(4\pi \mathbf {J} + {\frac {\parcial \mathbf {E} }{parcial t}}right). }  

Páginas relacionadas