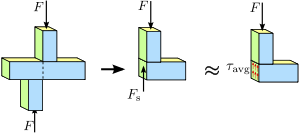Tensión mecánica
La tensión es la fuerza por unidad de superficie sobre un cuerpo que tiende a hacer que cambie de forma.
La tensión es una medida de las fuerzas internas de un cuerpo entre sus partículas. Estas fuerzas internas son una reacción a las fuerzas externas aplicadas sobre el cuerpo que provocan su separación, compresión o deslizamiento. Las fuerzas externas son fuerzas superficiales o fuerzas del cuerpo. La tensión es la fuerza media por unidad de superficie que una partícula de un cuerpo ejerce sobre una partícula adyacente, a través de una superficie imaginaria que las separa.
La fórmula para la tensión normal uniaxial es
σ = F A {\\Nsigma={frac {F}{A}}
donde σ es la tensión, F es la fuerza y A es la superficie.
En las unidades del SI, la fuerza se mide en newtons y el área en metros cuadrados. Esto significa que la tensión es newtons por metro cuadrado, o N/m2 . Sin embargo, la tensión tiene su propia unidad del SI, llamada pascal. 1 pascal (símbolo Pa) equivale a 1 N/m2 . En unidades imperiales, la tensión se mide en libras-fuerza por pulgada cuadrada, que a menudo se abrevia como "psi". La dimensión de la tensión es la misma que la de la presión.
En la mecánica del continuo, el cuerpo deformable cargado se comporta como un continuo. Así, estas fuerzas internas se distribuyen continuamente dentro del volumen del cuerpo material. (Esto significa que la distribución de esfuerzos en el cuerpo se expresa como una función continua a trozos en el espacio y el tiempo). Las fuerzas provocan la deformación de la forma del cuerpo. La deformación puede provocar un cambio de forma permanente o un fallo estructural si el material no es lo suficientemente resistente.
Algunos modelos de la mecánica del continuo tratan la fuerza como algo que puede cambiar. Otros modelos consideran la deformación de la materia y los cuerpos sólidos, porque las características de la materia y los sólidos son tridimensionales. Cada enfoque puede dar resultados diferentes. Los modelos clásicos de la mecánica del continuo suponen una fuerza media y no incluyen adecuadamente los "factores geométricos". (La geometría del cuerpo puede ser importante para saber cómo se reparte la tensión y cómo se acumula la energía durante la aplicación de la fuerza externa).
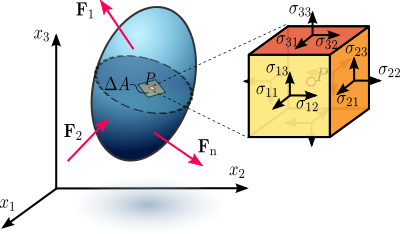
Figura 1.1 Esfuerzos en un cuerpo de material deformable cargado, asumido como un continuo.
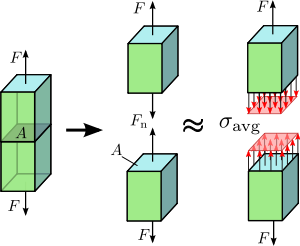
Figura 1.2 Tensión axial en una barra prismática cargada axialmente.
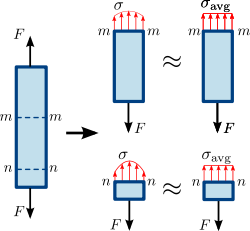
Figura 1.3 Tensión normal en una barra prismática (miembro recto de sección transversal uniforme). La distribución de tensiones o fuerzas en la sección transversal de la barra no es necesariamente uniforme. Sin embargo, una tensión normal media σ a v g {\displaystyle \sigma _{mathrm {avg} ¡}\,\! } 
Figura 1.4 Tensión de cizallamiento en una barra prismática. La distribución de esfuerzos o fuerzas en la sección transversal de la barra no es necesariamente uniforme. No obstante, un esfuerzo cortante medio τ a v g {{displaystyle \\tau _{mathrm {avg}} ¡}\,\! 
Tensión de cizallamiento
Más información: Tensión de cizallamiento
Tensiones simples
En algunas situaciones, la tensión dentro de un objeto puede describirse con un solo número, o con un solo vector (un número y una dirección). Tres de estas situaciones de tensión simple son la tensión normal uniaxial, la tensión de corte simple y la tensión normal isotrópica.
Tensión normal uniaxial
El esfuerzo de tracción (o tensión) es el estado de tensión que conduce a la expansión; es decir, la longitud de un material tiende a aumentar en la dirección de tracción. El volumen del material permanece constante. Cuando se aplican fuerzas iguales y opuestas sobre un cuerpo, la tensión debida a esta fuerza se denomina tensión de tracción.
Por lo tanto, en un material uniaxial la longitud aumenta en la dirección de la tensión de tracción y las otras dos direcciones disminuirán en tamaño. En el modo uniaxial de tensión, el esfuerzo de tracción es inducido por fuerzas de arrastre. La tensión de tracción es lo contrario de la tensión de compresión.
Los miembros estructurales en tensión directa son cuerdas, anclajes de suelo y clavos, pernos, etc. Las vigas sometidas a momentos de flexión pueden incluir esfuerzos de tracción, así como esfuerzos de compresión y/o esfuerzos cortantes.
La tensión de tracción puede aumentar hasta alcanzar la resistencia a la tracción, es decir, el estado límite de tensión.
Tensión en cuerpos unidimensionales
Todos los objetos reales ocupan un espacio tridimensional. Sin embargo, si dos dimensiones son muy grandes o muy pequeñas en comparación con las demás, el objeto puede modelarse como unidimensional. Esto simplifica la modelización matemática del objeto. Los objetos unidimensionales son, por ejemplo, un trozo de alambre cargado por los extremos y visto de lado, y una chapa metálica cargada por la cara y vista de cerca y a través de la sección transversal.
Páginas relacionadas
- Tensión
- Doblar
Preguntas y respuestas
P: ¿Qué es el estrés?
R: El estrés es la fuerza por unidad de superficie sobre un cuerpo que tiende a hacer que cambie de forma. Es una medida de las fuerzas internas de un cuerpo entre sus partículas, y es la fuerza media por unidad de superficie que una partícula de un cuerpo ejerce sobre una partícula adyacente a través de una superficie imaginaria que las separa.
P: ¿Cómo afectan las fuerzas externas a la tensión?
R: Las fuerzas externas son fuerzas superficiales o fuerzas del cuerpo, y provocan una deformación de la forma del cuerpo que puede conducir a un cambio de forma permanente o a un fallo estructural si el material no es lo suficientemente resistente.
P: ¿Cuál es la fórmula de la tensión normal uniaxial?
R: La fórmula de la tensión normal uniaxial es σ = F/A, donde σ es la tensión, F es la fuerza y A es la superficie. En las unidades del SI, la fuerza se mide en newtons y el área en metros cuadrados, lo que significa que la tensión sería newtons por metro cuadrado (N/m2). Sin embargo, existe su propia unidad SI para la tensión llamada pascal (Pa), que equivale a 1 N/m2. En unidades imperiales, se mediría en libras-fuerza por pulgada cuadrada (psi).
P: ¿Qué supone la mecánica del continuo sobre la fuerza?
R: Los modelos clásicos de la mecánica del continuo suponen una fuerza media y no incluyen adecuadamente los factores geométricos, lo que significa que no tienen en cuenta cómo afecta la geometría a la forma en que se acumula la energía durante la aplicación de una fuerza externa.
P: ¿Cómo es posible que distintos modelos den resultados diferentes al examinar la deformación de la materia y los cuerpos sólidos?
R: Los distintos modelos consideran la deformación de la materia y los cuerpos sólidos de forma diferente porque las características de la materia y los sólidos son tridimensionales, por lo que cada enfoque tiene en cuenta aspectos diferentes que pueden dar lugar a resultados distintos.
P: ¿Cómo trata la mecánica continua los cuerpos deformables con carga?
R: La mecánica continua trata los cuerpos deformables cargados como continuos - lo que significa que las fuerzas internas se distribuyen continuamente dentro del volumen del cuerpo material en lugar de concentrarse en ciertos puntos como ocurre con los modelos clásicos.
Buscar dentro de la enciclopedia