Momento magnético: qué es, fórmula, propiedades y ejemplos
Descubre qué es el momento magnético, su fórmula, propiedades y ejemplos claros. Guía práctica con conceptos, aplicaciones y cálculos paso a paso.
El momento magnético de un imán es una cantidad que determina la fuerza que el imán puede ejercer sobre las corrientes eléctricas y el par que un campo magnético ejercerá sobre él. Un bucle de corriente eléctrica, una barra magnética, un electrón, una molécula y un planeta tienen momentos magnéticos.
Tanto el momento magnético como el campo magnético pueden considerarse vectores que tienen una magnitud y una dirección. La dirección del momento magnético apunta desde el polo sur al norte de un imán. El campo magnético producido por un imán también es proporcional a su momento magnético. Más concretamente, el término momento magnético se refiere normalmente al momento dipolar magnético de un sistema, que produce el primer término en la expansión multipolar de un campo magnético general. El componente dipolar del campo magnético de un objeto es simétrico respecto a la dirección de su momento dipolar magnético y disminuye como el cubo inverso de la distancia al objeto.
Definición física y orientación
El momento magnético es un vector que caracteriza la intensidad y orientación del comportamiento magnético de un objeto. En elementos macroscópicos como un imán o una bobina, su dirección viene dada por la regla de la mano derecha: para una corriente que circula por un bucle, el vector momento magnético apunta según el eje del bucle en la dirección del pulgar si los dedos indican la dirección de la corriente.
Fórmulas principales
- Para un bucle de corriente plano único: μ = I·A·n, donde I es la corriente, A el área del bucle y n el vector unitario normal al plano del bucle (dirección dada por la regla de la mano derecha). Para N vueltas, μ = N·I·A.
- Torque ejercido por un campo magnético uniforme: τ = μ × B. Su magnitud es τ = μ B sinθ, con θ el ángulo entre μ y B.
- Energía potencial magnética de un dipolo en un campo magnético uniforme: U = −μ · B.
- Campo magnético lejos de un dipolo (campo de dipolo magnético en el vacío): B(r) = (μ0/4π) [ (3(μ·r) r)/r^5 − μ/r^3 ], donde μ0 es la permeabilidad del vacío y r el vector de posición respecto al dipolo.
- Fuerza sobre un dipolo magnético en un campo no uniforme (si μ es constante): F = ∇(μ · B).
- Para partículas con espín (electrón, nucleones): μ = γ S, donde S es el momento angular (espín u orbital) y γ la relación giromagnética (γ = g q / 2m, con g el factor giromagnético).
Unidades y constantes relevantes
- Unidad SI del momento magnético: A·m², que es equivalente a J/T (julios por tesla).
- Magnetón de Bohr (momento magnético característico del electrón): μB = eħ / (2 m_e) ≈ 9.274×10−24 J/T.
- Momento magnético del campo terrestre (orden de magnitud): ≈ 7.9×1022 A·m² (valor aproximado y sujeto a variaciones geofísicas).
Propiedades importantes
- El momento magnético es un vector y, para sistemas compuestos, los momentos magnéticos parciales se suman vectorialmente.
- En sistemas cuánticos el momento magnético está cuantizado: por ejemplo el espín del electrón produce momentos magnéticos con valores discretos relacionados con μB y con el factor g.
- El componente dipolar domina a distancias grandes; contribuciones multipolares superiores (cuadrupolar, etc.) decaen más rápida o lentamente según el orden.
- Un dipolo en un campo magnético no uniforme experimenta una fuerza neta —esto es la base de la separación de partículas magnéticas en dispositivos como el experimento de Stern–Gerlach o en trampas magnéticas.
Ejemplos y cálculo rápido
Ejemplo práctico: un bucle circular de radio 5 cm (0.05 m) con corriente I = 2 A y una sola vuelta. El área A = π r² ≈ π (0.05)² ≈ 7.85×10−3 m². El momento magnético es
μ = I·A = 2 × 7.85×10−3 ≈ 1.57×10−2 A·m².
Si ese bucle está en un campo magnético uniforme B = 0.1 T y el ángulo entre μ y B es 30°, el par (torque) es τ = μ B sin30° ≈ 1.57×10−2 × 0.1 × 0.5 ≈ 7.85×10−4 N·m.
Ejemplos físicos reales:
- Una bobina eléctrica con varias vueltas: aumenta μ proporcionalmente al número de vueltas N.
- Un imán de barra macroscópico: se modela frecuentemente como un dipolo magnético cuyos polos efectivos determinan su μ.
- Electrón en un átomo: tiene momentos magnéticos orbital y de espín; el orden de magnitud típico viene dado por el magnetón de Bohr μB.
- Planetas: la Tierra y otros planetas tienen momentos magnéticos generados por corrientes eléctricas en su interior.
Medición y aplicaciones
El momento magnético se mide con técnicas que detectan el par o el campo producido: magnetómetros de torsión, fluxgate, SQUID (Superconducting Quantum Interference Device) para momentos muy pequeños, y mediciones de fuerza en gradientes de campo. Sus aplicaciones incluyen motores eléctricos, sensores magnéticos, resonancia magnética, estudio de materiales magnéticos, astrofísica y geofísica.
En resumen, el momento magnético es una magnitud vectorial central para describir cómo un objeto responde a campos magnéticos y cómo genera dichos campos. Sus fórmulas simples (μ = I·A para bucles, τ = μ × B, U = −μ·B) permiten predecir fuerzas, pares y energías en multitud de sistemas desde componentes eléctricos hasta átomos y planetas.
Dos definiciones de momento
En los libros de texto se utilizan dos enfoques complementarios para definir los momentos magnéticos. En los libros de texto anteriores a 1930, se definían utilizando los polos magnéticos. Los libros de texto más recientes los definen en términos de corrientes ampèricas.
Definición de polo magnético
Los físicos representan las fuentes de momentos magnéticos en los materiales como polos. Los polos norte y sur son una analogía de las cargas positivas y negativas en la electrostática. Consideremos una barra magnética que tiene polos magnéticos de igual magnitud pero de polaridad opuesta. Cada polo es la fuente de una fuerza magnética que se debilita con la distancia. Como los polos magnéticos siempre vienen en pares, sus fuerzas se anulan parcialmente porque mientras un polo tira, el otro repele. Esta anulación es mayor cuando los polos están cerca, es decir, cuando la barra magnética es corta. La fuerza magnética producida por una barra magnética, en un punto determinado del espacio, depende, por tanto, de dos factores: tanto de la fuerza p {\displaystyle p} 
de sus polos, como del vector l {\displaystyle \mathbf {l} 
que los separa. El momento se define como
m = p l . {\displaystyle \mathbf {m} =p\mathbf {l} . } 
Apunta en la dirección del polo sur al polo norte. La analogía con los dipolos eléctricos no debe llevarse demasiado lejos porque los dipolos magnéticos están asociados al momento angular (véase Momento magnético y momento angular). Sin embargo, los polos magnéticos son muy útiles para los cálculos magnetostáticos, especialmente en las aplicaciones a los ferromagnetos. Los profesionales que utilizan el enfoque de los polos magnéticos generalmente representan el campo magnético por el campo irrotacional H {\displaystyle \mathbf {H} } 
en analogía con el campo eléctrico E {\displaystyle \mathbf {E} } 
.
Definición del bucle de corriente
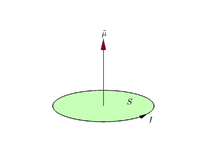
Supongamos que una espira cerrada plana transporta una corriente eléctrica I {\displaystyle I}
y tiene un área vectorial S {\displaystyle \mathbf {S}}. } 
( x {estilo de visualización x} 
, y {estilo de visualización y} 
y z {\displaystyle z}
de este vector son las áreas de las proyecciones del bucle sobre las coordenadas y z {\displaystyle yz} 
, z x {\displaystyle zx} 
y x y {\displaystyle xy}
). Su momento magnético m {\displaystyle \mathbf {m} } 
, vector, se define como:
m = I S . {\displaystyle \mathbf {m} =I\mathbf {S} . } 
Por convención, la dirección del área vectorial viene dada por la regla de agarre de la mano derecha (curvando los dedos de la mano derecha en la dirección de la corriente alrededor de la espira, cuando la palma de la mano está "tocando" el borde exterior de la espira, y el pulgar recto indica la dirección del área vectorial y, por tanto, del momento magnético).
Si el bucle no es plano, el momento se da como
m = I 2 ∫ r × d r . {\displaystyle \mathbf {m} = {\frac {I}{2}int \mathbf {r} \N - veces {\rm {d}} {mathbf {r} . } 
En el caso más general de una distribución de corriente arbitraria en el espacio, el momento magnético de dicha distribución se puede encontrar a partir de la siguiente ecuación:
m = 1 2 ∫ r × J d V , {\displaystyle \mathbf {m} ={\frac {1}{2}}int \mathbf {r} \N - veces \N -mathbf {J} \V,} 
donde r {\displaystyle \mathbf {r} 
es el vector de posición que apunta desde el origen a la ubicación del elemento de volumen, y J } es 
el vector de densidad de corriente en esa ubicación.
La ecuación anterior puede utilizarse para calcular el momento magnético de cualquier conjunto de cargas en movimiento, como un sólido cargado que gira, sustituyendo
J = ρ v , {\\Nmathbf {J} =\rho \mathbf {v} ,} 
donde ρ {\displaystyle \rho }
es la densidad de carga eléctrica en un punto determinado y v {\displaystyle \mathbf {v} } 
es la velocidad lineal instantánea de ese punto.
Por ejemplo, el momento magnético producido por una carga eléctrica que se mueve a lo largo de una trayectoria circular es
m = 1 2 q r × v {\displaystyle \mathbf {m} ={frac {1}{2}},q\\mathbf {r} \N - veces \Nmathbf {v} } 
,
donde r {\displaystyle \mathbf {r} } es la posición de la carga q {\displaystyle q}
respecto al centro del círculo y v {\displaystyle \mathbf {v} } es la velocidad instantánea de la carga.
Los profesionales que utilizan el modelo de bucle de corriente generalmente representan el campo magnético por el campo solenoide B {\displaystyle \mathbf {B}}. } 
análogo al campo electrostático D {\displaystyle \mathbf {D} } 
.
Momento magnético de un solenoide
Una generalización del bucle de corriente anterior es una bobina de varias vueltas, o solenoide. Su momento es la suma vectorial de los momentos de las vueltas individuales. Si el solenoide tiene N {\displaystyle N} 
vueltas idénticas (bobinado de una sola capa),
m = N I S . {\displaystyle \mathbf {m} =NI\mathbf {S} . } 
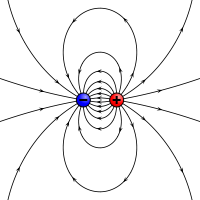
Un análogo electrostático de un momento magnético: dos cargas opuestas separadas por una distancia finita.
Momento m {\displaystyle \mathbf {m} de una espira de corriente plana con área S {estilo de visualización S} 
y corriente I {estilo de visualización I} .
Imagen tridimensional de un solenoide.
Unidades
La unidad para el momento magnético no es una unidad base en el Sistema Internacional de Unidades (SI) y puede representarse de más de una manera. Por ejemplo, en la definición del bucle de corriente, el área se mide en metros cuadrados e I {\displaystyle I} se mide en amperios, por lo que el momento magnético se mide en amperios-metros cuadrados ( A m 2 {\displaystyle {\text{A m}^{2}} 
). En la ecuación del par en un momento, el par se mide en Newton.metros y el campo magnético en tesla, por lo que el momento se mide en N.m por Tesla ( N.m T - 1 {\displaystyle {\text{N.m T}^{-1}} )
. Estas dos representaciones son equivalentes:
A m 2 = N.m T - 1 . {\displaystyle \\\a6}^{2}=,{\a6}^{1}. } 
En el sistema CGS, hay varios conjuntos diferentes de unidades de electromagnetismo, de los cuales los principales son ESU, Gauss y EMU. Entre ellas, hay dos unidades alternativas (no equivalentes) de momento dipolar magnético en CGS:
(ESU CGS) 1 statA-cm² = 3,33564095×10-14(m 2-A o N.m/T)
y (de uso más frecuente)
(EMU CGS y Gaussian-CGS) 1 erg/G = 1 abA-cm² = 10 -3(m 2-A o N.m/T).
La relación de estas dos unidades CGS no equivalentes (UEM/UCE) es igual exactamente a la velocidad de la luz en el espacio libre, expresada en cm/s.
Todas las fórmulas de este artículo son correctas en unidades del SI, pero en otros sistemas de unidades puede ser necesario cambiar las fórmulas. Por ejemplo, en unidades del SI, una espira de corriente con corriente I y área A tiene momento magnético I×A (ver más abajo), pero en unidades de Gauss el momento magnético es I×A/c.
| Momentos magnéticos intrínsecos y espines de algunas partículas elementales | ||
| Partículas | Momento dipolar magnético en unidades del SI (10 −27J/T) | Número cuántico de espín (adimensional) |
| -9284.764 | 1/2 | |
| protón | 14.106067 | 1/2 |
| neutrón | -9.66236 | 1/2 |
| muón | -44.904478 | 1/2 |
| deuterón | 4.3307346 | 1 |
| tritón | 15.046094 | 1/2 |
Para la relación entre las nociones de momento magnético y magnetización, véase magnetización.
Preguntas y respuestas
P: ¿Qué es el momento magnético de un imán?
R: El momento magnético de un imán es una magnitud que determina la fuerza que el imán puede ejercer sobre las corrientes eléctricas y el par que un campo magnético ejercerá sobre él.
P: ¿Qué objetos tienen momentos magnéticos?
R: Un bucle de corriente eléctrica, una barra magnética, un electrón, una molécula y un planeta tienen momentos magnéticos.
P: ¿Cómo se pueden considerar tanto el momento magnético como el campo magnético?
R: Tanto el momento magnético como el campo magnético pueden considerarse vectores que tienen una magnitud y una dirección.
P: ¿En qué dirección apunta el momento magnético en un imán?
R: La dirección del momento magnético apunta del polo sur al polo norte de un imán.
P: ¿Cuál es la relación entre el momento magnético y el campo magnético de un imán?
R: El campo magnético producido por un imán es proporcional a su momento magnético.
P: ¿A qué se refiere normalmente el término momento magnético?
R: Más concretamente, el término momento magnético se refiere normalmente al momento dipolar magnético de un sistema, que produce el primer término en la expansión multipolar de un campo magnético general.
P: ¿Cómo se comporta el componente dipolar del campo magnético de un objeto a medida que aumenta la distancia al objeto?
R: El componente dipolar del campo magnético de un objeto es simétrico respecto a la dirección de su momento dipolar magnético, y disminuye como el cubo inverso de la distancia al objeto.
Buscar dentro de la enciclopedia