Espiral logarítmica (equiangular): definición, historia y ejemplos
Descubre la espiral logarítmica: definición, historia desde Descartes y Bernoulli, y ejemplos en la naturaleza y ciencia. Aprende por qué es la 'Spira mirabilis'.
La espiral logarítmica, también llamada espiral equiangular o espiral de crecimiento, es un tipo especial de curva espiral que aparece con frecuencia en la naturaleza y en diversas aplicaciones científicas y artísticas. Fue descrita por primera vez por Descartes y estudiada en profundidad por Jakob Bernoulli, quien la denominó Spira mirabilis ("la espiral maravillosa").
Definición matemática
En coordenadas polares la espiral logarítmica se expresa por la fórmula
r = a · e^{bθ}
donde a > 0 es un factor de escala, b (real) determina la tasa de crecimiento radial y θ es el ángulo polar. En coordenadas cartesianas se puede parametrizar como
x(θ) = a · e^{bθ} · cos θ,
y(θ) = a · e^{bθ} · sin θ.
La propiedad más característica es que el ángulo entre el vector radial (la recta que une el origen con un punto de la curva) y la tangente a la espiral es constante. Si ese ángulo se denota por α, entonces
tan α = 1 / b
Propiedades importantes
- Auto‑similaridad: al rotar la espiral un cierto ángulo Δθ se obtiene la misma figura pero escalada por un factor e^{bΔθ}. Por eso la espiral es invariante por similitudes (combinaciones de rotación y homotecia).
- Equiangularidad: el ángulo entre la tangente y el radio vector es constante a lo largo de toda la curva.
- Relación con la exponencial compleja: en el plano complejo la espiral puede verse como la imagen de una recta bajo la función exponencial: z(θ) = a e^{(b + i)θ}.
- Transformaciones conformes e inversión: bajo una inversión respecto a un círculo (transformación z ↦ 1/z) una espiral logarítmica se transforma en otra espiral logarítmica (con parámetros relacionados).
- Crecimiento logarítmico: el radio crece (o decrece) exponencialmente con el ángulo; por eso cada vuelta aumenta el tamaño en proporción fija.
Historia y anécdotas
Aunque Descartes fue uno de los primeros en describir este tipo de espiral, Jakob Bernoulli la estudió con especial interés a finales del siglo XVII y la llamó Spira mirabilis. La espiral fascinó a Bernoulli por su propiedad de invariancia bajo escalado y rotación; según la tradición, pidió que se grabara en su tumba junto con la inscripción "Eadem mutata resurgo" ("A pesar de cambiado, resurjo igual").
Ejemplos en la naturaleza y aplicaciones
- Conchas y estructuras biológicas: muchas conchas de moluscos y caparazones muestran un crecimiento que aproxima la forma de una espiral logarítmica, aunque no siempre es una coincidencia exacta.
- Brazos de galaxias y sistemas astronómicos: las estructuras espirales de ciertas galaxias y la forma de huracanes recuerdan la geometría logarítmica.
- Arquitectura y arte: la propiedad estética de la espiral y su escalado constante la hacen popular en diseño y composición.
- Espiral áurea (golden spiral): es una espiral logarítmica particular en la que el factor de crecimiento entre vueltas separadas por un ángulo de π/2 es la razón áurea φ. Se obtiene eligiendo b tal que e^{b(π/2)} = φ; es frecuente en referencias culturales aunque muchas afirmaciones sobre su presencia exacta en la naturaleza son aproximaciones.
Cómo dibujarla y visualizarla
Para dibujar una espiral logarítmica basta tomar un rango de ángulos θ (por ejemplo, desde θ = −4π hasta θ = 4π) y trazar los puntos (x(θ), y(θ)) usando las fórmulas anteriores. Variando el parámetro b se controla la apertura de la espiral: valores pequeños de |b| producen espirales más abiertas (ángulo α cercano a 90°), y valores grandes de |b| producen espirales más cerradas (ángulo α pequeño).
En resumen, la espiral logarítmica combina belleza y simplicidad matemática: su equiangularidad y auto‑similitud la hacen un objeto central en geometría, en modelos de crecimiento y en fenómenos naturales donde aparecen patrones repetitivos en distintas escalas.
Los brazos de las galaxias espirales suelen tener la forma de una espiral logarítmica, aquí la Galaxia del Remolino.
Una zona de bajas presiones sobre Islandia muestra un patrón espiral aproximadamente logarítmico.
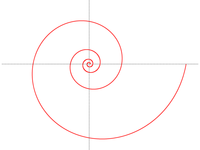
Espiral logarítmica (paso de 10°)
Corte de una concha de nautilus que muestra las cámaras dispuestas en una espiral aproximadamente logarítmica
Definición
En coordenadas polares (r, θ) la curva puede escribirse como
r = a e b θ {\displaystyle r=ae^{b\theta }\}, } 
o
θ = 1 b ln ( r / a ) , {\displaystyle \theta ={frac {1}{b}\ln(r/a),} 
de ahí el nombre "logarítmico". En forma paramétrica, la curva es
x ( t ) = r cos ( t ) = a e b t cos ( t ) {\displaystyle x(t)=r\cos(t)=ae^{bt}\cos(t)\},} 
y ( t ) = r sin ( t ) = a e b t sin ( t ) {\displaystyle y(t)=r\sin(t)=ae^{bt}\sin(t)\},} 
con números reales a y b.
La espiral tiene la propiedad de que el ángulo ɸ entre la tangente y la línea radial en el punto (r,θ) es constante. Esta propiedad se puede expresar en términos geométricos diferenciales como
arccos ⟨ r ( θ ) , r ′ ( θ ) ⟩ ‖ r ( θ ) ‖ ‖ r ′ ( θ ) ‖ = arctan 1 b = ϕ , {\displaystyle \arccos {\frac {\langle \mathbf {r} (\theta ),|mathbf {r} '(\theta )||rangle }{|mathbf {r} (\theta )||||mathbf {r} '(\theta )||}=arctan {\frac {1}{b}=phi ,} 
La derivada r'(θ) es proporcional al parámetro b. En otras palabras, controla lo "apretada" que está la espiral y en qué dirección. En el caso extremo de que b = 0 (ɸ = π/2) la espiral se convierte en un círculo de radio a. Por el contrario, en el límite en que b se acerca al infinito (ɸ → 0) la espiral tiende a una línea recta. El complemento de ɸ se llama paso.
Spira mirabilis y Jakob Bernoulli
Spira mirabilis, "espiral milagrosa" en latín, es otro nombre para la espiral logarítmica. Aunque esta curva ya había sido bautizada por otros matemáticos, el nombre de espiral "milagrosa" o "maravillosa" se lo dio Jakob Bernoulli, porque le fascinaba una de sus propiedades matemáticas únicas: el tamaño de la espiral aumenta, pero la forma se mantiene igual con cada curva añadida. Quizá por esta propiedad, la espira mirabilis ha evolucionado en la naturaleza, viéndose en algunos seres vivos, como las conchas de los nautilos y las cabezas de los girasoles. Jakob Bernoulli quería esta forma en su lápida, pero, por error, se colocó en su lugar una espiral de Arquímedes.
Espirales logarítmicas en la naturaleza
En varios fenómenos naturales se pueden encontrar curvas que están cerca de ser espirales logarítmicas. A continuación, algunos ejemplos y razones:
- La aproximación de un halcón a su presa. Su vista más aguda se encuentra en un ángulo con respecto a su dirección de vuelo; este ángulo es el mismo que la inclinación de la espiral.
- La aproximación de un insecto a una fuente de luz. Están acostumbrados a que la fuente de luz esté en un ángulo constante respecto a su trayectoria de vuelo. Por lo general, el sol es la única fuente de luz y volando de esa manera se obtiene una línea prácticamente recta.
- Los brazos de las galaxias espirales. Se cree que nuestra propia galaxia, la Vía Láctea, tiene cuatro brazos espirales principales, cada uno de los cuales es aproximadamente una espiral logarítmica con un ángulo de inclinación de unos 12 grados, un ángulo de inclinación inusualmente pequeño para una galaxia como la Vía Láctea. En general, los brazos de las galaxias espirales tienen ángulos de inclinación que oscilan entre 10 y 40 grados.
- Los brazos de los ciclones tropicales, como los huracanes.
|
|
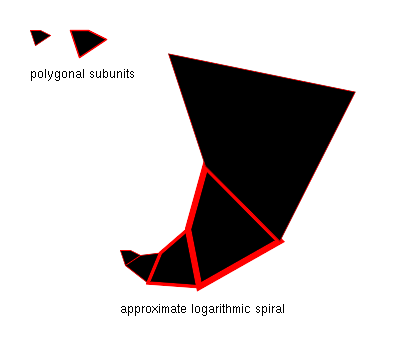
- Muchas estructuras biológicas, incluidas las telas de araña y las conchas de los moluscos. En estos casos, la razón es la siguiente: Comience con cualquier figura bidimensional de forma irregular F0 . Expanda F0 por un cierto factor para obtener F1 , y coloque F1 junto a F0 , de modo que dos lados se toquen. Ahora expande F1 por el mismo factor para obtener F2 , y colócalo junto a F1 como antes. Repitiendo esto se obtendrá una espiral logarítmica aproximada cuyo paso está determinado por el factor de expansión y el ángulo con el que se colocaron las figuras una al lado de la otra. Esto se muestra para las figuras poligonales en el gráfico adjunto.
Páginas relacionadas
- Secuencia de Fibonacci
- Dispositivo de leva con muelle
Buscar dentro de la enciclopedia