Serie armónica (matemática)

En matemáticas, la serie armónica es la serie infinita divergente:

∑ n = 1 ∞ 1 n = 1 + 1 2 + 1 3 + 1 4 + 1 5 + ⋯ {{displaystyle }{suma _{n=1}^{infty }{{frac {1}{n}=1+{frac {1}{3}+{frac {1}{4}+{frac {1}{5}+{cdots } $\sum _{n=1}^{\infty }{\frac {1}{n}}=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+\cdots$

Divergente significa que a medida que se añaden más términos la suma no deja de aumentar. No va hacia un único valor finito.

Infinito significa que siempre se puede añadir otro término. No hay un término final en la serie.

Su nombre proviene de la idea de los armónicos en la música: las longitudes de onda de los sobretonos de una cuerda que vibra son 1/2,

1/3, 1/4, etc., de la longitud de onda fundamental de la cuerda. Aparte del primer término, cada término de la serie es la media armónica de los términos que están a su lado. La expresión media armónica también proviene de la música.

Historia

El hecho de que la serie armónica diverge fue demostrado por primera vez en el siglo XIV por Nicole Oresme, pero fue olvidado. Las pruebas fueron dadas en el siglo XVII por Pietro Mengoli, Johann Bernoulli y Jacob Bernoulli.

Las secuencias armónicas han sido utilizadas por los arquitectos. En el periodo barroco los arquitectos las utilizaron en las proporciones de las plantas, los alzados y en las relaciones entre los detalles arquitectónicos de iglesias y palacios.

Divergencia

Hay varias pruebas conocidas de la divergencia de la serie armónica. A continuación se exponen algunas de ellas.

Prueba de comparación

Una forma de demostrar la divergencia es comparar la serie armónica con otra serie divergente, en la que cada denominador se sustituye por la siguiente mayor potencia de dos:

1 + 1 2 + 1 3 + 1 4 + 1 5 + 1 6 + 1 7 + 1 8 + 1 9 + ⋯ ≥ 1 + 1 2 + 1 4 + 1 4 + 1 8 + 1 8 + 1 8 + 1 8 + 1 16 + ⋯ {\displaystyle {\begin{aligned}&{}1+{1}{2}+{1}{3}+{1}{4}+{1}{5}+{1}{6}+{1}{8}+{1}{9}+{cdots}{12pt}{geq}.1+{{refrac {1}{2}}+{{color}{rojo}{mathbf {4}} {{frac}{1}{4}+{frac}{color}{rojo}{mathbf}{8} {{frac}} {color {rojo} {mathbf {8}} {{frac}}1}{color rojo}{mathbf}{8}} {{frac}{1}{8}}+{frac}{color}{rojo}{mathbf}{16}} {{cdots}}+{end{aligned}} ${\begin{aligned}&{}1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+{\frac {1}{6}}+{\frac {1}{7}}+{\frac {1}{8}}+{\frac {1}{9}}+\cdots \\[12pt]\geq {}&1+{\frac {1}{2}}+{\frac {1}{\color {red}{\mathbf {4} }}}+{\frac {1}{4}}+{\frac {1}{\color {red}{\mathbf {8} }}}+{\frac {1}{\color {red}{\mathbf {8} }}}+{\frac {1}{\color {red}{\mathbf {8} }}}+{\frac {1}{8}}+{\frac {1}{\color {red}{\mathbf {16} }}}+\cdots \end{aligned}}$

Cada término de la serie armónica es mayor o igual que el término correspondiente de la segunda serie, y por tanto la suma de la serie armónica debe ser mayor o igual que la suma de la segunda serie. Sin embargo, la suma de la segunda serie es infinita:

1 + ( 1 2 ) + ( 1 4 + 1 4 ) + ( 1 8 + 1 8 + 1 8 + 1 8 ) + ( 1 16 + ⋯ + 1 16 ) + ⋯ = 1 + 1 2 + 1 2 + 1 2 + ⋯ = ∞ {\displaystyle {\begin{aligned}&{}1+\a la izquierda({\frac {1}{2}{dirección})+\a la izquierda({\frac {1}{4}{dirección})+\NIzquierda({\frac {1}{4}}derecha)+\NIzquierda({\frac {1}{8}}+\N-izquierda({{8}}) +\N-cierre de filas({1}{8}}) +\N-izquierda({{16}}) +\N-cierre de filas({1}{16}) ${\begin{aligned}&{}1+\left({\frac {1}{2}}\right)+\left({\frac {1}{4}}\!+\!{\frac {1}{4}}\right)+\left({\frac {1}{8}}\!+\!{\frac {1}{8}}\!+\!{\frac {1}{8}}\!+\!{\frac {1}{8}}\right)+\left({\frac {1}{16}}\!+\!\cdots \!+\!{\frac {1}{16}}\right)+\cdots \\[12pt]={}&1+{\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{2}}+\cdots =\infty \end{aligned}}$

Se deduce (por la prueba de comparación) que la suma de la serie armónica debe ser también infinita. Más precisamente, la comparación anterior demuestra que

∑ n = 1 2 k 1 n ≥ 1 + k 2 {\displaystyle \sum _{n=1}^{2^{k}} {\frac {1}{n}}geq 1+{\frac {k}{2}} $\sum _{n=1}^{2^{k}}{\frac {1}{n}}\geq 1+{\frac {k}{2}}$

para cada número entero positivo $k$ .

Esta prueba, propuesta por Nicole Oresme hacia 1350, se considera un punto álgido de la matemática medieval. Todavía hoy es una prueba estándar que se enseña en las clases de matemáticas.

Prueba integral

Es posible demostrar que la serie armónica diverge comparando su suma con una integral impropia. Considere la disposición de rectángulos que se muestra en la figura de la derecha. Cada rectángulo tiene 1 unidad de ancho y

1/n unidades de altura, por lo que el área total del número infinito de rectángulos es la suma de la serie armónica:

área de los rectángulos = 1 + 1 2 + 1 3 + 1 4 + 1 5 + ⋯ {\displaystyle {\begin{array}{c}{texto}{área de} {{texto}{rectángulos}{end{array}}=1+{frac {1}{2}+{frac {1}{3}+{frac {1}{4}+{frac {1}{5}+\cdots } ${\begin{array}{c}{\text{area of}}\\{\text{rectangles}}\end{array}}=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+\cdots$

El área total bajo la curva $y =$

1/x de 1 a infinito viene dada por una integral impropia divergente:

área bajo la curva = ∫ 1 ∞ 1 x d x = ∞ . {\displaystyle {\begin{array}{c}{texto{área bajo}{{texto{curva}{end{array}}=int _{1}^{infty }{frac {1}{x}},dx={infty .} ${\begin{array}{c}{\text{area under}}\\{\text{curve}}\end{array}}=\int _{1}^{\infty }{\frac {1}{x}}\,dx=\infty .$

Dado que esta área está contenida en su totalidad dentro de los rectángulos, el área total de los rectángulos debe ser también infinita. Esto demuestra que

∑ n = 1 k 1 n > ∫ 1 k + 1 1 x d x = ln ( k + 1 ) . {\displaystyle \\Nsuma _{n=1}^{k}{frac {1}{n}}>int _{1}^{k+1}{frac {1}{x}},dx=\ln(k+1).} $\sum _{n=1}^{k}{\frac {1}{n}}>\int _{1}^{k+1}{\frac {1}{x}}\,dx=\ln(k+1).$

La generalización de este argumento se conoce como la prueba integral.

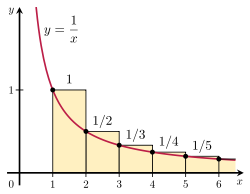
Ilustración de la prueba integral.

Tasa de divergencia

La serie armónica diverge muy lentamente. Por ejemplo, la suma de los 10 primeros términos de⁴³ es inferior a 100. Esto se debe a que las sumas parciales de la serie tienen un crecimiento logarítmico. En particular,

∑ n = 1 k 1 n = ln k + γ + ε k ≤ ( ln k ) + 1 {\displaystyle \sum _{n=1}^{k}{\frac {1}{n}=\ln k+\gamma +\varepsilon _{k}\leq (\ln k)+1} $\sum _{n=1}^{k}{\frac {1}{n}}=\ln k+\gamma +\varepsilon _{k}\leq (\ln k)+1$

donde γ es la constante de Euler-Mascheroni y ε $k ~$

1/2k que se aproxima a 0 a medida que $k va$ al infinito. Leonhard Euler demostró esto y también que la suma que incluye sólo los recíprocos de los primos también diverge, es decir:

∑ p prime 1 p = 1 2 + 1 3 + 1 5 + 1 7 + 1 11 + 1 13 + 1 17 + ⋯ = ∞ . {\displaystyle \\\aquella suma _{{prima}} {{frac {1}{p}}={frac {1}{2}}+{frac {1}{3}}+{frac {1}{5}}+{frac {1}{7}}+{frac {1}{11}}+{frac {1}{13}}+{frac {1}{17}}+{cdots} ={infty .} $\sum _{p{\text{ prime }}}{\frac {1}{p}}={\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{5}}+{\frac {1}{7}}+{\frac {1}{11}}+{\frac {1}{13}}+{\frac {1}{17}}+\cdots =\infty .$

Sumas parciales

Los primeros treinta números armónicos
$n$	Suma parcial de la serie armónica, $H n$
$n$	expresado como una fracción		decimal	tamaño relativo
1	1		~1	1
2	3	/2	~1.5	1.5
3	11	/6	~1.83333	1.83333
4	25	/12	~2.08333	2.08333
5	137	/60	~2.28333	2.28333
6	49	/20	~2.45	2.45
7	363	/140	~2.59286	2.59286
8	761	/280	~2.71786	2.71786
9	7129	/2520	~2.82897	2.82897
10	7381	/2520	~2.92897	2.92897
11	83711	/27720	~3.01988	3.01988
12	86021	/27720	~3.10321	3.10321
13	1145993	/360360	~3.18013	3.18013
14	1171733	/360360	~3.25156	3.25156
15	1195757	/360360	~3.31823	3.31823
16	2436559	/720720	~3.38073	3.38073
17	42142223	/12252240	~3.43955	3.43955
18	14274301	/4084080	~3.49511	3.49511
19	275295799	/77597520	~3.54774	3.54774
20	55835135	/15519504	~3.59774	3.59774
21	18858053	/5173168	~3.64536	3.64536
22	19093197	/5173168	~3.69081	3.69081
23	444316699	/118982864	~3.73429	3.73429
24	1347822955	/356948592	~3.77596	3.77596
25	34052522467	/8923714800	~3.81596	3.81596
26	34395742267	/8923714800	~3.85442	3.85442
27	312536252003	/80313433200	~3.89146	3.89146
28	315404588903	/80313433200	~3.92717	3.92717
29	9227046511387	/2329089562800	~3.96165	3.96165
30	9304682830147	/2329089562800	~3.99499	3.99499

Las sumas parciales finitas de las series armónicas divergentes,

H n = ∑ k = 1 n 1 k , {\displaystyle H_{n}={suma _{k=1}^{n}{frac {1}{k},} $H_{n}=\sum _{k=1}^{n}{\frac {1}{k}},$

se denominan números armónicos.

La diferencia entre $H n$ y $ln n$ converge a la constante de Euler-Mascheroni. La diferencia entre dos números armónicos cualesquiera nunca es un número entero. Ningún número armónico es un número entero, excepto $H 1 = 1$ .

Series relacionadas

Series armónicas alternas

La serie

∑ n = 1 ∞ ( - 1 ) n + 1 n = 1 - 1 2 + 1 3 - 1 4 + 1 5 - ⋯ {{displaystyle}} suma _{n=1}^{\infty}}{{frac {(-1)^{n+1}{n}=1-{frac {1}{2}+{frac {1}{3}}-{frac {1}{4}+{frac {1}{5}{cdots}} $\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}=1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+{\frac {1}{5}}-\cdots$

se conoce como la serie armónica alterna. Esta serie converge por la prueba de la serie alterna. En particular, la suma es igual al logaritmo natural de 2:

1 - 1 2 + 1 3 - 1 4 + 1 5 - ⋯ = ln 2. {\displaystyle 1-{frac {1}{2}}+{frac {1}{3}}-{frac {1}{4}}+{frac {1}{5}}-\cdots =\ln 2.} $1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+{\frac {1}{5}}-\cdots =\ln 2.$

La serie armónica alterna, aunque es condicionalmente convergente, no es absolutamente convergente: si los términos de la serie se reordenan sistemáticamente, en general la suma se vuelve diferente y, dependiendo del reordenamiento, posiblemente incluso infinita.

La fórmula de la serie armónica alterna es un caso especial de la serie de Mercator, la serie de Taylor para el logaritmo natural.

Se puede derivar una serie relacionada a partir de la serie de Taylor para la arctangente:

∑ n = 0 ∞ ( - 1 ) n 2 n + 1 = 1 - 1 3 + 1 5 - 1 7 + ⋯ = π 4 . {\displaystyle \\\Nsum _{n=0}^{\infty }{{frac {(-1)^{n}}{2n+1}}=1-{{frac {1}{3}}+{{frac {1}{5}}-{{1}{7}}+\cdots ={{frac {\pi}{4}}. $\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}=1-{\frac {1}{3}}+{\frac {1}{5}}-{\frac {1}{7}}+\cdots ={\frac {\pi }{4}}.$

Esto se conoce como la serie de Leibniz.

Series armónicas generales

La serie armónica general es de la forma

∑ n = 0 ∞ 1 a n + b , {\displaystyle \\sum _{n=0}^{\infty }{\frac {1}{an+b}},} $\sum _{n=0}^{\infty }{\frac {1}{an+b}},$

donde $a \neq 0$ y $b$ son números reales, y

b/a no es cero ni un entero negativo.

Por la prueba de comparación de límites con las series armónicas, todas las series armónicas generales también divergen.

$serie p$

Una generalización de la serie armónica es la $serie p$ (o serie hiperarmónica), definida como

∑ n = 1 ∞ 1 n p {{displaystyle \\\Nsum _{n=1}^{\infty }{\frac {1}{n^{p}}}} $\sum _{n=1}^{\infty }{\frac {1}{n^{p}}}$

para cualquier número real $p$ . Cuando $p = 1$ , la serie $p$ es la serie armónica, que diverge. La prueba integral o la prueba de condensación de Cauchy muestran que la serie $p$ converge para todo $p > 1$ (en cuyo caso se llama serie sobrearmónica) y diverge para todo $p \leq 1$ . Si $p > 1$ entonces la suma de la serie $p$ es $ζ(p), es decir$ , la función zeta de Riemann evaluada en $p$ .

El problema de encontrar la suma para $p = 2$ se llama el problema de Basilea; Leonhard Euler demostró que es

$π$ ² /6. El valor de la suma para $p = 3$ se llama constante de Apéry, ya que Roger Apéry demostró que es un número irracional.

serie ln

Relacionada con la $serie p$ está la serie ln, definida como

∑ n = 2 ∞ 1 n ( ln n ) p {\displaystyle \\Nsum _{n=2}^{{infty}}{frac {1}{n(\ln n)^{p}}}} $\sum _{n=2}^{\infty }{\frac {1}{n(\ln n)^{p}}}$

para cualquier número real positivo $p. Se$ puede demostrar mediante la prueba integral que diverge para $p \leq 1$ pero converge para todo $p > 1$ .

$Serie φ$

Para cualquier función convexa y de valor real φ tal que

lim sup u → 0 + φ ( u 2 ) φ ( u ) < 1 2 , {\displaystyle \limsup _{u\\\a 0^{+}}{frac {\varphi \left({\frac {u}{2}\right)}{{varphi (u)}}<{{frac {1}{2}}, } $\limsup _{u\to 0^{+}}{\frac {\varphi \left({\frac {u}{2}}\right)}{\varphi (u)}}<{\frac {1}{2}},$

la serie

∑ n = 1 ∞ φ ( 1 n ) {\displaystyle \\Nsum _{n=1}^{infty }\\\Nvarphi \Nleft({\frac {1}{n}\Nright)} $\sum _{n=1}^{\infty }\varphi \left({\frac {1}{n}}\right)$

es convergente.

Series armónicas aleatorias

La serie armónica aleatoria

∑ n = 1 ∞ s n n , {\displaystyle \\\Nsum _{n=1}^{\infty }{\frac {s_{n}},} $\sum _{n=1}^{\infty }{\frac {s_{n}}{n}},$

donde las $s n$ son variables aleatorias independientes e idénticamente distribuidas que toman los valores +1 y -1 con igual probabilidad

1/2, es un ejemplo bien conocido en la teoría de la probabilidad para una serie de variables aleatorias que converge con probabilidad 1. El hecho de esta convergencia es una consecuencia fácil del teorema de las tres series de Kolmogorov o de la desigualdad máxima de Kolmogorov, estrechamente relacionada. Byron Schmuland, de la Universidad de Alberta, examinó además las propiedades de la serie armónica aleatoria y demostró que la serie convergente es una variable aleatoria con algunas propiedades interesantes. En particular, la función de densidad de probabilidad de esta variable aleatoria evaluada en +2 o en -2 toma el valor 0,12499999999999999999999999764..., diferenciándose de 1/8 en menos de 10⁻⁴² . El artículo de Schmuland explica por qué esta probabilidad se acerca tanto, pero no exactamente, a 1/8. El valor exacto de esta probabilidad viene dado por la integral del producto coseno infinito $C 2$ dividido por π.

Series armónicas agotadas

Se puede demostrar que la serie armónica agotada en la que se eliminan todos los términos en los que aparece el dígito 9 en cualquier parte del denominador converge y su valor es inferior a 80. De hecho, cuando se eliminan todos los términos que contienen cualquier cadena de dígitos (en cualquier base) la serie converge.

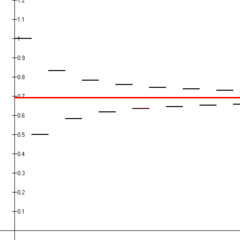
Se muestran las primeras catorce sumas parciales de la serie armónica alterna (segmentos de línea negra) que convergen al logaritmo natural de 2 (línea roja).

Aplicaciones

La serie armónica puede ser contraintuitiva. Esto se debe a que es una serie divergente aunque los términos de la serie se hagan más pequeños y vayan hacia el cero. La divergencia de la serie armónica es la fuente de algunas paradojas.

El "gusano de la banda elástica". Supongamos que un gusano se arrastra a lo largo de una banda de goma de un metro de elasticidad infinita al mismo tiempo que la banda de goma se estira uniformemente. Si el gusano recorre 1 centímetro por minuto y la banda se estira 1 metro por minuto, ¿llegará el gusano alguna vez al final de la banda elástica? La respuesta, contraintuitivamente, es "sí", ya que después de $n$ minutos, la relación entre la distancia recorrida por el gusano y la longitud total de la banda elástica es

1 100 ∑ k = 1 n 1 k . {\displaystyle {\frac {1}{100}}suma _{k=1}^{n}{\frac {1}{k}}.} ${\frac {1}{100}}\sum _{k=1}^{n}{\frac {1}{k}}.$

Dado que la serie se hace arbitrariamente grande a medida que $n$ se hace más grande, eventualmente esta relación debe exceder de 1, lo que implica que el gusano alcanza el final de la banda elástica. Sin embargo, el valor de $n$ en el que esto ocurre debe ser extremadamente grande: aproximadamente e $100$ , un número superior a 10⁴³ minutos (10³⁷ años). Aunque la serie armónica sí diverge, lo hace muy lentamente.

El problema del Jeep pregunta cuánto combustible total se necesita para que un coche con una capacidad limitada de transporte de combustible cruce un desierto dejando gotas de combustible a lo largo de la ruta. La distancia que el coche puede recorrer con una cantidad determinada de combustible está relacionada con las sumas parciales de las series armónicas, que crecen logarítmicamente. Así, el combustible necesario aumenta exponencialmente con la distancia deseada.

El problema del apilamiento de bloques: dada una colección de fichas de dominó idénticas, es posible apilarlas en el borde de una mesa de manera que cuelguen sobre el borde de la mesa sin caerse. El resultado contraintuitivo es que se pueden apilar de forma que el saliente sea tan grande como se quiera. Es decir, siempre que haya suficientes fichas de dominó.

Un nadador que va más rápido cada vez que toca la pared de la piscina. El nadador comienza a cruzar una piscina de 10 metros a una velocidad de 2 m/s, y con cada cruce, se añaden otros 2 m/s a la velocidad. En teoría, la velocidad del nadador es ilimitada, pero el número de cruces de la piscina necesarios para llegar a esa velocidad es muy grande; por ejemplo, para llegar a la velocidad de la luz (ignorando la relatividad especial), el nadador necesita cruzar la piscina 150 millones de veces. Contrariamente a este gran número, el tiempo necesario para alcanzar una velocidad determinada depende de la suma de las series en cualquier número de cruces de la piscina:

10 2 ∑ k = 1 n 1 k . {\displaystyle {\frac {10}{2}}suma _{k=1}^{n}{\frac {1}{k}}.} ${\frac {10}{2}}\sum _{k=1}^{n}{\frac {1}{k}}.$

El cálculo de la suma muestra que el tiempo necesario para llegar a la velocidad de la luz es de sólo 97 segundos.

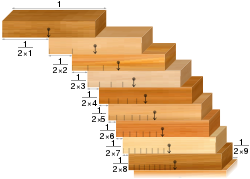
El problema del apilamiento de bloques: los bloques alineados según la serie armónica tienden un puente sobre las hendiduras de cualquier anchura.

Páginas relacionadas

Progresión armónica
Lista de sumas de recíprocos

Preguntas y respuestas

P: ¿Qué es la serie armónica?

R: La serie armónica es una serie divergente infinita en la que cada término es igual a 1 dividido por su posición en la secuencia.

P: ¿Qué significa que una serie sea divergente?

R: Divergente significa que a medida que se añaden más términos, la suma no deja de aumentar y no se dirige hacia un único valor finito.

P: ¿Qué significa que una serie sea infinita?

R: Infinita significa que siempre se puede añadir otro término y que no hay un término final en la serie.

P: ¿De dónde viene el nombre de esta serie?

R: El nombre de esta serie viene de la idea de los armónicos en la música, donde las longitudes de onda de los sobretonos son 1/2, 1/3, 1/4, etc., de la longitud de onda fundamental de la cuerda.

P: ¿Qué es una media armónica?

R: Una media armónica es cuando cada término de una secuencia es igual a la media armónica de sus términos vecinos. Esta frase también proviene de la música.

P: ¿Cómo calculamos cada término de esta secuencia?

R: Cada término de esta secuencia se puede calcular dividiendo uno por su posición en la secuencia (1/n).