Serie de Taylor: definición, teorema y aplicaciones en cálculo

Aprende la serie de Taylor: definición clara, teorema, demostraciones y aplicaciones prácticas en cálculo, física e informática. Ejemplos y ejercicios paso a paso.

Autor: Leandro Alegsa

02-03-2026 12:24

Una serie de Taylor es una idea que se utiliza en informática, cálculo, química, física y otros tipos de matemáticas de nivel superior. Es una serie que se utiliza para crear una estimación (conjetura) de cómo es una función. También existe un tipo especial de serie de Taylor llamada serie de Maclaurin.

La teoría que subyace a la serie de Taylor es que si se elige un punto en el plano de coordenadas (ejes x e y), es posible adivinar cómo será una función en el área que rodea a ese punto. Esto se hace tomando las derivadas de la función y sumándolas todas. La idea es que es posible sumar el número infinito de derivadas y llegar a una única suma finita.

En matemáticas, una serie de Taylor muestra una función como la suma de una serie infinita. Los términos de la suma se toman de las derivadas de la función. Las series de Taylor provienen del teorema de Taylor.

Definición y fórmula

Sea f una función que tiene derivadas de todos los órdenes en un entorno del punto a. La serie de Taylor centrada en a está dada por la suma:

f(x) = Σ_{n=0}^∞ (f^{(n)}(a) / n!) · (x − a)^n,

donde f^{(n)}(a) representa la n-ésima derivada evaluada en a y n! es el factorial de n. Cuando a = 0 esta serie recibe el nombre de serie de Maclaurin.

Polinomio de Taylor y resto

El polinomio de Taylor de grado n (también llamado polinomio de aproximación) es la suma truncada:

P_n(x) = Σ_{k=0}^n (f^{(k)}(a) / k!) · (x − a)^k.

La diferencia entre la función y este polinomio se llama resto o término de error R_n(x). Una forma práctica y muy utilizada para estimar el resto es la forma de Lagrange:

R_n(x) = f^{(n+1)}(ξ) / (n+1)! · (x − a)^{n+1},

donde ξ está entre a y x. Esta expresión permite acotar el error si conocemos una cota para la derivada de orden n+1 en el intervalo considerado.

Condiciones de convergencia y funciones analíticas

Convergencia: que la serie de Taylor exista formalmente (es decir, que todas las derivadas existan) no garantiza que la serie converja al valor de la función para x ≠ a. Para que la serie represente la función es necesario además que el resto R_n(x) → 0 cuando n → ∞ en un intervalo alrededor de a.
Radio de convergencia: para funciones reales o complejas, la serie de Taylor tiene un radio de convergencia r ≥ 0 (posible r = ∞). Dentro del intervalo |x − a| < r la serie converge absolutamente; fuera de él diverge.
Funciones analíticas: si la función coincide con su serie de Taylor en un entorno de a, se dice que es analítica en ese punto. Hay funciones infinitamente diferenciables que no son analíticas (un ejemplo clásico es f(x) = e^{-1/x^2} para x ≠ 0 y f(0)=0: todas sus derivadas en 0 son cero, por lo que su serie de Taylor en 0 es la serie nula, que no coincide con la función salvo en x=0).

Ejemplos clásicos

Exponencial: e^x = 1 + x + x^2/2! + x^3/3! + …, converge para todo x (r = ∞).
Seno y coseno (Maclaurin): sin x = x − x^3/3! + x^5/5! − … ; cos x = 1 − x^2/2! + x^4/4! − …, ambas convergen para todo x.
Logaritmo (en torno a 1): ln(1 + x) = x − x^2/2 + x^3/3 − …, válido para |x| < 1 (y con condiciones en los extremos).

Aplicaciones prácticas

Aproximaciones numéricas: calcular valores de funciones con polinomios (útil cuando se dispone de calculadoras, ordenadores o para integrales y derivadas aproximadas).
Linealización: el polinomio de grado 1 (la aproximación lineal) se usa para aproximar funciones cerca de un punto y es la base para métodos como Newton-Raphson para resolver ecuaciones.
Métodos numéricos: en integración y solución de ecuaciones diferenciales se utilizan series para construir métodos de alta precisión y estimar errores.
Física y química: en mecánica y teoría de perturbaciones se expanden potenciales y funciones alrededor de estados de equilibrio para simplificar problemas complejos.
Informática: aproximación de funciones en bibliotecas matemáticas, optimización de código y análisis de algoritmos mediante expansiones locales.

Consejos prácticos para usar series de Taylor

Elige el punto a (centro) cercano al intervalo donde necesitas precisión.
Controla el error con la expresión del resto o usando el siguiente término omitido como estimación. Si el término siguiente es pequeño, la aproximación suele ser buena.
Conoce el radio de convergencia: una expansión válida en un punto puede no ser útil lejos de ese punto.
En problemas reales combine la teoría con pruebas numéricas: comparar con valores exactos o con mayor grado ayuda a validar la aproximación.

Resumen

La serie de Taylor es una herramienta fundamental en cálculo y en muchas áreas aplicadas para aproximar funciones por polinomios usando sus derivadas. Entender su fórmula, el polinomio truncado y el resto permite emplearla de forma segura en cálculos y estimaciones. Sin embargo, hay que verificar la convergencia y recordar que no todas las funciones infinitamente diferenciables coinciden con su serie de Taylor en un entorno.

Historia

El filósofo de la antigua Grecia Zenón de Elea fue el primero que tuvo la idea de esta serie. La paradoja llamada "parodia de Zenón" el resultado. Creía que era imposible sumar un número infinito de valores y obtener como resultado un único valor finito.

Otro filósofo griego, Aristóteles, dio una respuesta a la cuestión filosófica. Sin embargo, fue Arquímedes quien aportó una solución matemática utilizando su método de agotamiento. Consiguió demostrar que cuando algo se divide en un número infinito de trozos diminutos, éstos seguirán sumando un único conjunto cuando se vuelvan a sumar. El antiguo matemático chino Liu Hui demostró lo mismo varios cientos de años después.

Los primeros ejemplos conocidos de la serie de Taylor son los trabajos de Mādhava de Sañgamāgrama en la India en el año 1300. Los matemáticos indios posteriores escribieron sobre su trabajo con las funciones trigonométricas de seno, coseno, tangente y arctangente. Hoy en día no existe ningún escrito o registro de Mādhava. Otros matemáticos se basaron en los descubrimientos de Mādhava y trabajaron más con estas series hasta el año 1500.

James Gregory, un matemático escocés, trabajó en este campo en la década de 1600. Gregory estudió las series de Taylor y publicó varias series de Maclaurin. En 1715, Brook Taylor descubrió un método general para aplicar la serie a todas las funciones. (Todas las investigaciones anteriores mostraban cómo aplicar el método sólo a funciones específicas). Colin Maclaurin publicó un caso especial de la serie de Taylor en la década de 1700. Esta serie, que se basa en el cero, se llama serie de Maclaurin.

Definición

Una serie de Taylor puede utilizarse para describir cualquier función ƒ(x) que sea una función suave (o, en términos matemáticos, "infinitamente diferenciable"). La serie de Taylor se utiliza entonces para describir el aspecto de la función en la vecindad de algún número a.

Esta serie de Taylor, escrita como una serie de potencias, parece:

¡f ( a ) + f ′ ( a ) 1 ! ¡( x - a ) + f ″ ( a ) 2 ! ¡( x - a ) 2 + f ( 3 ) ( a ) 3 ! ( x - a ) 3 + ⋯ . {\displaystyle f(a)+{\frac {f'(a)}{1!}}(x-a)+{\frac {f''(a)}{2!}}(x-a)^{2}+{\frac {f^(3)}(a)}{3!}}(x-a)^{3}+\cdots . } $f(a)+{\frac {f'(a)}{1!}}(x-a)+{\frac {f''(a)}{2!}}(x-a)^{2}+{\frac {f^{(3)}(a)}{3!}}(x-a)^{3}+\cdots .$

Esta fórmula también se puede escribir en notación sigma como

¡∑ n = 0 ∞ f ( n ) ( a ) n ! ( x - a ) n {\displaystyle \\\Nsum _{n=0}^\\Ninfty }{frac {f^(n)}(a)}{n!}},(x-a)^{n} $\sum _{n=0}^{\infty }{\frac {f^{(n)}(a)}{n!}}\,(x-a)^{n}$

Aquí n! es el factorial de n. ƒ⁽ⁿ⁾ (a) es la enésima derivada de ƒ en el punto a. a {\displaystyle a} es un número en el dominio de la función. Si la serie de Taylor de una función es igual a esa función, la función se llama "función analítica".

Serie Maclaurin

Cuando a = 0 {\displaystyle a=0} $a=0$ la función se llama serie de Maclaurin. La serie de Maclaurin escrita como una serie de potencias tiene el siguiente aspecto:

f ( 0 ) + f ′ ( 0 ) 1 ! x + f ″ ( 0 ) 2 ! x 2 + f ( 3 ) ( 0 ) 3 ! x 3 + ⋯ . {\displaystyle f(0)+{\frac {f'(0)}{1!}}x+{\frac {f'(0)}{2!}}x^{2}+{\frac {f^(3)}(0)}{3!}}+\cdots . } $f(0)+{\frac {f'(0)}{1!}}x+{\frac {f''(0)}{2!}}x^{2}+{\frac {f^{(3)}(0)}{3!}}x^{3}+\cdots .$

Cuando se escribe en notación sigma, la serie de Maclaurin es:

¡∑ n = 0 ∞ f ( n ) ( 0 ) n ! x n {\displaystyle \\\Nsum _{n=0}^\\Ninfty }{frac {f^{(n)}(0)}{n!}} $\sum _{n=0}^{\infty }{\frac {f^{(n)}(0)}{n!}}\,x^{n}$

Imágenes principales

Algunas series importantes de Taylor y Maclaurin son las siguientes.

¡sin x = ∑ n = 0 ∞ ( - 1 ) n ( 2 n + 1 ) ! ¡x 2 n + 1 = x - x 3 3 ! ¡+ x 5 5 ! - ⋯ para todo x {\displaystyle \sin x=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n+1)!}}x^{2n+1}=x-{\frac {x^3}{3!}+{\frac {x^{5}{5!}}-\cdots {\text{ para todo}{x\! } $\sin x=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n+1)!}}x^{2n+1}=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-\cdots {\text{ for all }}x\!$

¡cos x = ∑ n = 0 ∞ ( - 1 ) n ( 2 n ) ! ¡x 2 n = 1 - x 2 2 ! ¡+ x 4 4 ! - ⋯ para todo x {\displaystyle \cos x={suma _{n=0}^{infty}}{{{1)^{n}}{2n}!}}x^{2n}=1-{{frac {x^{2}}{2!}}+{{frac {x^{4}}{4!}}-\cdots {\text{ para todo}{x}} } $\cos x=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n)!}}x^{2n}=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-\cdots {\text{ for all }}x\!$

¡sinh ( x ) = ∑ n = 0 ∞ 1 ( 2 n + 1 ) ! x 2 n + 1 para todo x {\displaystyle \sinh(x)={suma _{n=0}^{{infty }{{frac {1}{(2n+1)!}}x^{2n+1}{text{ para todo}{x}} } $\sinh(x)=\sum _{n=0}^{\infty }{\frac {1}{(2n+1)!}}x^{2n+1}{\text{ for all }}x\!$

¡cosh ( x ) = ∑ n = 0 ∞ 1 ( 2 n ) ! x 2 n para todo x {\displaystyle \cosh(x)={suma _{n=0}^{\infty }{{frac {1}(2n)!}}x^{{2n}{texto{ para todo}{x! } $\cosh(x)=\sum _{n=0}^{\infty }{\frac {1}{(2n)!}}x^{2n}{\text{ for all }}x\!$

¡e x = ∑ n = 0 ∞ 1 n ! x n = 1 + x + 1 2 ! x 2 + 1 3 ! x 3 + ⋯ para todo x {\displaystyle e^{x}=suma _{n=0}^{\infty}{frac {1}{n!}}x^{n}=1+x+{\frac {1}{2!}}x^{2}+{{\frac {1}{3!}}x^{3}+\cdots {\text{ para todo}}{x! } $e^{x}=\sum _{n=0}^{\infty }{\frac {1}{n!}}x^{n}=1+x+{\frac {1}{2!}}x^{2}+{\frac {1}{3!}}x^{3}+\cdots {\text{ for all }}x\!$

1 1 - x = ∑ n = 0 ∞ x n = 1 + x + x 2 + x 3 + x 4 + ⋯ para todo | x | < 1 {\displaystyle {\frac {1}{1-x}= suma _{n=0}^\infty }x^{n}=1+x+x^{2}+x^{4}+\cdots {\text{ para todo }|x|<1} ${\frac {1}{1-x}}=\sum _{n=0}^{\infty }x^{n}=1+x+x^{2}+x^{3}+x^{4}+\cdots {\text{ for all }}|x|<1$

ln ( 1 + x ) = ∑ n = 1 ∞ ( - 1 ) n + 1 n x n para todo | x | < 1 {\displaystyle \ln(1+x)=\sum _{n=1}^{\infty }{frac {(-1)^{n+1}{}x^{n}{text{ para todo }|x|<1} $\ln(1+x)=\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}x^{n}{\text{ for all }}|x|<1$

¡tan x = ∑ n = 1 ∞ B 2 n ( - 4 ) n ( 1 - 4 n ) ( 2 n ) ! ¡x 2 n - 1 = x + x 3 3 + 2 x 5 15 + ⋯ para | x | < π 2 {\displaystyle \tan x={suma _{n=1}^{\infty }{\frac {B_{2n}(-4)^{n}(1-4^{n})}{(2n)!}}x^{2n-1}=x+{\frac {x^{3}}+{{\frac {2x^{5}}{15}}+{\cdots {\text{para}}|x|<{\frac {\pi }{2}}} } $\tan x=\sum _{n=1}^{\infty }{\frac {B_{2n}(-4)^{n}(1-4^{n})}{(2n)!}}x^{2n-1}=x+{\frac {x^{3}}{3}}+{\frac {2x^{5}}{15}}+\cdots {\text{ for }}|x|<{\frac {\pi }{2}}\!$

Donde B n {\displaystyle B_{n}} $B_{n}$ es el enésimo número de Bernoulli, y ln {\displaystyle \ln } $\ln$ es el logaritmo natural.

[
{[96606-96606]}]

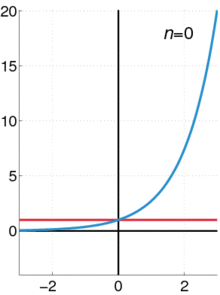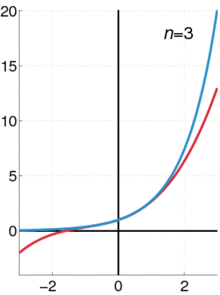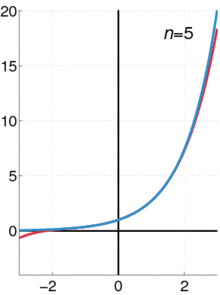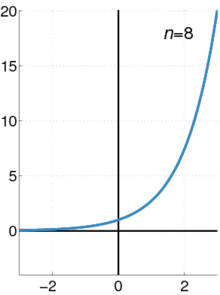
Una animación que muestra cómo se puede utilizar una serie de Taylor para aproximar una función. La línea azul muestra la función exponencial f ( x ) = e x {\displaystyle f(x)=e^{x}}. $f(x)=e^{x}$ . Las líneas rojas muestran la suma de n derivadas, es decir, n+1 términos de la serie de Taylor. A medida que n aumenta, la línea roja se acerca a la línea azul.

Buscar dentro de la enciclopedia