Función de densidad de probabilidad: qué es, propiedades y cálculo

Descubre qué es una función de densidad de probabilidad, sus propiedades clave y cómo calcularla paso a paso para interpretar distribuciones continuas y obtener probabilidades precisas.

Autor: Leandro Alegsa

22-12-2025 16:13

En probabilidad y estadística, una función de densidad de probabilidad es una función que caracteriza cualquier distribución de probabilidad continua. Para una variable aleatoria X, la función de densidad de probabilidad de X se escribe a veces como f X ( x ) {\displaystyle f_{X}(x)} $f_{X}(x)$ . La integral de la función de densidad de probabilidad en el intervalo [ a , b ] {\displaystyle [a,b]} $[a,b]$ produce la probabilidad de que una variable aleatoria dada con la densidad dada esté contenida en el intervalo proporcionado. Por definición, la función de densidad de probabilidad es no negativa en todo su dominio, en el que la integral suma 1.

Propiedades fundamentales

No negatividad: f_X(x) ≥ 0 para todo x.
Normalización: la integral total es 1, es decir, ∫_{-∞}^{∞} f_X(x) dx = 1.
Probabilidades por integración: para a ≤ b, P(a ≤ X ≤ b) = ∫_a^b f_X(x) dx. En variables continuas los extremos inclusivos o exclusivos no cambian el valor de la probabilidad.
Relación con la función de distribución acumulada (FDA): si F_X(x) es la FDA, entonces F_X(x) = ∫_{-∞}^{x} f_X(t) dt y, cuando F_X es diferenciable, f_X(x) = F_X'(x).
Valor puntual: para cualquier valor x0, P(X = x0) = 0 en una distribución continua (salvo que exista una parte discreta o singular).

Cálculo de probabilidades y ejemplos

Para calcular una probabilidad se evalúa la integral de la densidad en el intervalo deseado. Ejemplos sencillos:

Uniforme continua en [a, b]: f(x) = 1/(b − a) para a ≤ x ≤ b y 0 fuera. Entonces P(c ≤ X ≤ d) = (d − c)/(b − a) si a ≤ c < d ≤ b.
Exponencial con parámetro λ > 0 (soporte [0, ∞)): f(x) = λ e^{−λ x} para x ≥ 0. La probabilidad P(X ≥ t) = e^{−λ t}.
Normal (gaussiana) con media μ y varianza σ²: f(x) = (1/(σ√(2π))) e^{−(x−μ)²/(2σ²)}; las probabilidades se obtienen mediante integrales que normalmente se evalúan con la tabla de la normal estándar o funciones especiales.

Esperanza, varianza y momentos

Esperanza (media): E[X] = ∫_{-∞}^{∞} x f_X(x) dx, siempre que la integral exista (sea finita).
Varianza: Var(X) = E[(X − E[X])²] = ∫_{-∞}^{∞} (x − μ)² f_X(x) dx.
Momentos de orden k: E[X^k] = ∫ x^k f_X(x) dx, cuando convergen.

Cambio de variable

Si Y = g(X) con g monótona y diferenciable, la densidad de Y se obtiene por la fórmula de cambio de variable: f_Y(y) = f_X(g^{-1}(y)) · |d/dy g^{-1}(y)|. Para transformaciones no monótonas se suman las contribuciones de las ramas inversas.

Condiciones y casos especiales

Una función debe ser medible, no negativa y normalizable (integral igual a 1) para ser una densidad válida.
Existen distribuciones mixtas que combinan parte continua (con densidad) y parte discreta (con masa en puntos). También hay distribuciones singulares cuya masa está concentrada en conjuntos de medida nula; estas no se describen completamente mediante una densidad clásica.

Interpretación práctica

El valor f_X(x) no es una probabilidad, sino una densidad: indica cuán concentrada está la probabilidad alrededor de x. Cuanto mayor sea f_X(x), mayor será la probabilidad de encontrar valores de X cerca de x por unidad de longitud. Para obtener probabilidades hay que integrar f_X sobre el intervalo de interés.

Ejemplo numérico corto

Si X ∼ Uniforme(0,1), f_X(x)=1 para 0≤x≤1. Entonces P(0.2 ≤ X ≤ 0.7)=∫_{0.2}^{0.7} 1 dx = 0.5. La esperanza es E[X]=1/2 y la varianza Var(X)=1/12.

Notas finales

Las funciones de densidad son una herramienta central para modelar fenómenos continuos en probabilidad y estadística. Su correcta comprensión —especialmente la distinción entre densidad y probabilidad puntual, y la forma de calcular expectativas mediante integrales— es esencial para análisis y aplicaciones prácticas en ciencias, ingeniería, economía y otras áreas.

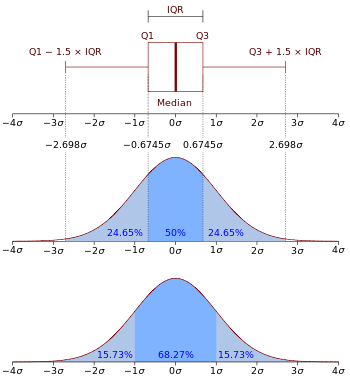
Boxplot y función de densidad de probabilidad de una distribución normal N(0, σ2 ) .

Densidad de probabilidad frente a función de masa de probabilidad

La función de masa de probabilidad es a una distribución de probabilidad discreta lo que la función de densidad de probabilidad es a una distribución de probabilidad continua. La función de densidad de probabilidad es necesaria para poder trabajar con distribuciones continuas.

Una variable aleatoria con una distribución de probabilidad continua puede tomar cualquier valor dentro de esa distribución. Al lanzar un dado se obtienen los números del 1 al 6, con una probabilidad de 1 6 ${\tfrac {1}{6}}$ , pero ésta no es una función continua, ya que sólo son posibles los números del 1 al 6.

Por el contrario, dos personas no tendrán la misma altura ni el mismo peso. Utilizando una función de densidad de probabilidad, es posible determinar la probabilidad para las personas entre 180 centímetros (71 in) y 181 centímetros (71 in), o entre 80 kilogramos (176,4 lb) y 81 kilogramos (178,6 lb), aunque haya infinitos valores entre estos dos límites.

Páginas relacionadas

Función de distribución acumulativa

Preguntas y respuestas

P: ¿Qué es una función de densidad de probabilidad?

R: Una función de densidad de probabilidad es una función que caracteriza cualquier distribución de probabilidad continua.

P: ¿Cómo se escribe la función de densidad de probabilidad de una variable aleatoria X?

R: La función de densidad de probabilidad de X se escribe a veces como f_X(x).

P: ¿Qué representa la integral de la función de densidad de probabilidad?

R: La integral de la función de densidad de probabilidad representa la probabilidad de que una variable aleatoria dada con la densidad dada esté contenida en un intervalo proporcionado.

P: ¿La función de densidad de probabilidad es siempre no negativa en todo su dominio?

R: Sí, por definición, la función de densidad de probabilidad es no negativa en todo su dominio.

P: ¿La integración sobre un intervalo suma 1?

R: Sí, la integración sobre un intervalo suma 1.

P: ¿Qué tipo de distribución caracteriza una función de densidad de probabilidad?

R: Una función de densidad de probabilidad caracteriza cualquier distribución de probabilidad continua.

Buscar dentro de la enciclopedia