Euclides de Alejandría: vida y obras del padre de la geometría
Descubre la vida y obras de Euclides de Alejandría, el padre de la geometría: su legado, aportes y la influencia de sus Elementos en la ciencia y la educación.
Euclides de Alejandría (en griego: Εὐκλείδης) (alrededor del año 325 a.C. - 265 a.C.) fue un matemático griego que vivió en Alejandría, Egipto, y trabajó en la Biblioteca de Alejandría. Se sabe poco de esta persona, pero se cree que vivió allí cuando Ptolomeo I era faraón. No se sabe dónde ni cuándo nació.
Vida y contexto histórico
La información biográfica sobre Euclides es escasa y proviene principalmente de autores tardíos como Proclo y Pappus. Según estas fuentes, ejerció la docencia en Alejandría y dirigió una escuela geométrica que influyó en generaciones posteriores. Vivió en el período helenístico, cuando la ciudad de Alejandría era un importante centro intelectual bajo la dinastía ptolemaica; por ello suele situarse su actividad alrededor del siglo III a. C. Ciertas anécdotas tradicionales —como la famosa respuesta a un rey que le preguntó si no había un camino real para aprender geometría, y Euclides replicó que “no existe un camino real para la geometría”— subrayan la reputación de rigor y método atribuida a su enseñanza, aunque estas historias proceden de testimonios posteriores.
Obras principales
La obra fundamental atribuida a Euclides es Los Elementos (Stoicheia), un compendio sistemático de la matemática de su tiempo organizado de forma axiomática. Los Elementos constan de trece libros que abarcan:
- definiciones, postulados y nociones comunes;
- geometría plana (triángulos, rectas, polígonos);
- teoría de proporciones y magnitudes (incluyendo el tratamiento de irracionales, heredado de Eudoxo);
- aritmética y teoría de números (donde aparece el algoritmo que hoy llamamos euclidiano);
- geometría de los sólidos.
Además de los Elementos, a Euclides se le atribuyen otros tratados que se conservan total o parcialmente, como el Data (sobre datos geométricos), obras sobre óptica y astronomía práctica (Phaenomena), así como otros escritos mencionados por autores antiguos. Existen también referencias a trabajos perdidos, por ejemplo los llamados porismata.
Método y aportaciones
La gran aportación de Euclides no fue tanto la invención de nuevas propiedades geométricas como la organización lógica de resultados mediante definiciones, postulados y proposiciones demostradas con rigurosidad. Entre sus aportaciones más destacadas están:
- la sistematización de la geometría en forma axiomática, que sirvió de modelo para la práctica matemática durante más de dos milenios;
- la formulación y uso del método deductivo —se parte de postulados para deducir teoremas—;
- la exposición del procedimiento hoy conocido como algoritmo euclidiano para calcular el máximo común divisor;
- la clara exposición del problema de la paralela y la famosa quinta postulado (postulado de las paralelas), cuyo estatus llevó siglos más tarde al desarrollo de geometrías no euclidianas cuando se mostró que podía reemplazarse por otras formulaciones.
Recepción e influencia
Los Elementos se convirtieron en el libro de texto por excelencia de la matemática; fue copiado, comentado y traducido extensamente. Durante la Edad Media el texto circuló tanto en el mundo islámico —donde matemáticos y traductores árabes elaboraron comentarios y versiones— como en Europa, con traducciones al latín y múltiples ediciones impresas a partir del siglo XV. La influencia de la obra de Euclides se extendió más allá de las matemáticas: su modelo axiomático influyó en la filosofía, la lógica y la formación científica en general.
Fuentes históricas y problemas de atribución
La escasez de datos contemporáneos obliga a confiar en comentaristas posteriores (Proclo, Pappus, Eutocio, entre otros) para reconstruir la figura de Euclides. Por ello, resulta difícil separar con total certeza la autoría de algunas obras atribuidas a él y precisar fechas exactas. La mayor parte de los historiadores acepta, no obstante, que la persona conocida como Euclides fue el compilador y organizador de los conocimientos geométricos que hoy llevamos en los Elementos.
Legado
Euclides ha pasado a la historia como el “padre de la geometría” por la perdurabilidad y la claridad de su obra. Su enfoque axiomático y su insistencia en la demostración formal marcaron un antes y un después en la manera de presentar la matemática. Aunque la aparición de las geometrías no euclidianas en el siglo XIX mostró los límites de su sistema en relación con la estructura del espacio físico, su método sigue siendo fundamento en la enseñanza de la geometría y en la concepción moderna de prueba matemática.
Lecturas y ediciones
Los Elementos han sido objeto de innumerables ediciones, traducciones y comentarios desde la Antigüedad hasta la actualidad. Para un estudio crítico conviene consultar ediciones modernas que aporten traducción y comentario histórico-filosófico, además de las ediciones críticas de los textos griegos y de las versiones árabes y latinas que muestran la cadena de transmisión del texto.

Estatua de Euclides, en el Museo de Historia Natural de Oxford
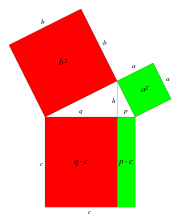
Ilustración del teorema más famoso de Euclides, el teorema de Pitágoras: el cuadrado de la hipotenusa de un triángulo rectángulo es igual a la suma de los cuadrados de los otros dos lados
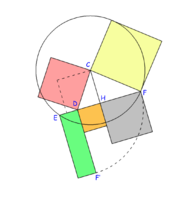
Libro III de los Elementos de Euclides, Proposición 35: "Si en una circunferencia se cortan dos rectas, entonces el rectángulo contenido por los segmentos de la una es igual al rectángulo contenido por los segmentos de la otra"
Los elementos
Euclides reunió todo lo que se sabía de la geometría, que forma parte de las matemáticas. Sus Elementos son la principal fuente de la geometría antigua. Los libros de texto basados en Euclides se han utilizado hasta hoy. En el libro, parte de un pequeño conjunto de axiomas (es decir, un grupo de cosas que todo el mundo considera ciertas). A continuación, Euclides muestra las propiedades de los objetos geométricos y de los números enteros, basándose en esos axiomas.
Los Elementos también incluyen trabajos sobre la perspectiva, las secciones cónicas, la geometría esférica y, posiblemente, las superficies cuádricas. Además de la geometría, la obra incluye también la teoría de los números. Euclides inventó la idea de los máximos comunes divisores. Aparecen en sus Elementos. El máximo común divisor de dos números es el mayor número que puede caber uniformemente en los dos números.
El sistema geométrico descrito en los Elementos fue durante mucho tiempo conocido simplemente como geometría, y se consideraba la única geometría posible. Hoy en día ese sistema se denomina geometría euclidiana para distinguirlo de otras geometrías llamadas no euclidianas que los matemáticos desarrollaron en el siglo XIX.
Otros trabajos
Además de los Elementos, han llegado hasta nuestros días al menos cinco obras de Euclides. Siguen la misma estructura lógica que los Elementos, con definiciones y proposiciones demostradas.
- Los datos tratan de la naturaleza y las implicaciones de la información "dada" en los problemas geométricos; el tema está estrechamente relacionado con los cuatro primeros libros de los Elementos.
- Sobre las divisiones de las figuras, que sólo se conserva parcialmente traducido al árabe, se refiere a la división de las figuras geométricas en dos o más partes iguales o en partes de determinada proporción. Es similar a una obra del siglo III d.C. de Herón de Alejandría.
- La catóptrica, que trata de la teoría matemática de los espejos, en particular de las imágenes formadas en espejos cóncavos planos y esféricos. La atribución a Euclides es dudosa. Su autor pudo ser Teón de Alejandría.
- En griego se conserva Phaenomena, un tratado de astronomía esférica, bastante similar a Sobre la esfera en movimiento de Autólico de Pitane, que floreció hacia el 310 a.C.
Homenaje a Euclides

Uno de los fragmentos más antiguos que se conservan de los Elementos de Euclides, fechado hacia el año 100 de nuestra era. El diagrama acompaña a la Proposición 5 del Libro II.
Buscar dentro de la enciclopedia