Dimensión: qué es, tipos y ejemplos en matemáticas y física
Descubre qué es la dimensión, sus tipos y ejemplos en matemáticas y física: de 1D a espacios vectoriales y 4D (tiempo). Conceptos claros y ejemplos prácticos.
Las dimensiones son las maneras en que describimos, medimos y experimentamos el mundo: arriba y abajo, derecha e izquierda, adelante y atrás, caliente y frío, cuánto pesa y cuánto mide algo. También aparecen en conceptos más abstractos de las matemáticas y la física. Una forma intuitiva de entender una dimensión es como un grado de libertad: la dirección independiente en la que un objeto o un punto puede desplazarse dentro de un espacio. Existen distintos usos del término “dimensión” según el contexto (geometría, álgebra lineal, topología, física, teoría de fractales, análisis dimensional), y no hay una única definición que abarque todas las intuiciones posibles.
Dimensión en álgebra lineal (espacios vectoriales)
En un espacio vectorial 
(donde los vectores pueden imaginarse como "flechas" con dirección y magnitud), la dimensión de , escrita también como 
, es igual a la cardinalidad (el número de vectores) de una base de V . Es decir, la dimensión indica cuántas direcciones independientes (vectores base) hacen falta para generar todo el espacio. También puede interpretarse como el tamaño del mayor conjunto de vectores linealmente independientes del espacio.
Ejemplos sencillos
- Dimensión 0 (0D): un punto. No tiene extensión, sólo ubicación.
- Dimensión 1 (1D): una recta o una curva (por ejemplo, una línea). Sólo hay una dirección independiente (adelante/atrás).
- Dimensión 2 (2D): un plano, como una hoja de papel. Dos direcciones independientes (longitud y anchura).
- Dimensión 3 (3D): el espacio ordinario en el que vivimos. Tres direcciones independientes (longitud, anchura y profundidad); los matemáticos llaman a este caso espacio euclidiano.
- Dimensión 4 (4D) en física: añadir el tiempo como coordenada junto a las espaciales da lugar al concepto de espacio-tiempo (4D), que permite ubicar un acontecimiento por su posición espacial y temporal.
Dimensión como medida de posición y coordenadas
Las posiciones se representan por coordenadas que indican distancias en las direcciones de longitud, anchura y altura; estas distancias son una medida de la posición relativa respecto a un origen. En contextos físicos se habla de coordenadas y métricas que permiten calcular la distancia entre puntos en distintos tipos de espacios.
Otras nociones de dimensión en matemáticas
Además de la dimensión lineal (álgebra), existen otros conceptos útiles:
- Dimensión topológica: definida mediante refinamientos de cubiertas abiertas o por la propiedad de separar conjuntos; mide la complejidad topológica de un espacio.
- Dimensión de Hausdorff (fractal): puede tomar valores no enteros y describe cómo escala el tamaño de un objeto cuando se observa a diferentes escalas; útil para fractales (por ejemplo, la curva de Koch tiene dimensión mayor que 1 pero menor que 2).
- Dimensión de Minkowski / capacidad: otra forma de cuantificar la complejidad de un conjunto en el plano o en el espacio.
Estos conceptos permiten describir objetos que no encajan en la clasificación entera 0,1,2,3 (por ejemplo, conjuntos fractales, la costa de una isla o el conjunto de Cantor).
Dimensión en física y unidades fundamentales
En física “dimensión” a menudo se refiere a las magnitudes físicas básicas (por ejemplo: longitud, masa, tiempo) y a cómo se combinan en una ecuación. El Sistema Internacional (SI) identifica siete unidades base que representan dimensiones físicas fundamentales:
- Longitud (metro, m)
- Masa (kilogramo, kg)
- Tiempo (segundo, s)
- Intensidad de corriente eléctrica (ampere, A)
- Temperatura termodinámica (kelvin, K)
- Cantidad de sustancia (mol)
- Intensidad luminosa (candela, cd)
Las ecuaciones físicas deben ser homogéneas en dimensiones: ambos lados de una igualdad deben tener las mismas dimensiones (por ejemplo, no es coherente sumar una longitud y un tiempo). Esta regla permite comprobar la plausibilidad de fórmulas y deducir relaciones entre variables mediante el análisis dimensional.
Análisis dimensional y ejemplos prácticos
El análisis dimensional se usa para verificar fórmulas y reducir el número de parámetros independientes en un problema físico (teorema de Buckingham Π). Ejemplo clásico: el periodo T de un péndulo simple depende de la longitud L y la gravedad g. Por análisis dimensional se deduce que T es proporcional a sqrt(L/g), salvo un factor adimensional (2π para pequeñas oscilaciones).
Dimensión y grados de libertad
Hablar de dimensión equivale a contar los grados de libertad de un sistema: el número de coordenadas independientes necesarias para describir por completo su estado. En mecánica, por ejemplo, una partícula libre en el espacio 3D tiene 3 grados de libertad. En dinámica estadística o mecánica clásica, el espacio de fases de N partículas tiene dimensión proporcional a 6N (posiciones y momentos en 3D por partícula).
Resumen y consejos para distinguir usos
- Matemáticas (álgebra): dimensión = número de vectores en una base, número de direcciones independientes.
- Matemáticas (topología/fractales): existen nociones que capturan estructura y escalado, pueden ser no enteras.
- Física: dimensión física = tipo de magnitud (longitud, masa, tiempo...) y su tratamiento mediante unidades; espacio-tiempo suele modelarse como 4D en relatividad.
Comprender qué significado de “dimensión” aplica en cada contexto evita confusiones: en álgebra es un número entero que mide independencia lineal; en física puede ser tanto la dimensión espacial/temporal como la dimensión de magnitudes físicas (unidades); en teoría de fractales puede ser un valor no entero que refleja comportamiento a distintas escalas.
Un diagrama de las cuatro primeras dimensiones espaciales.
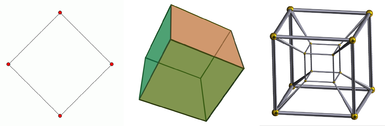
De izquierda a derecha, el cuadrado, el cubo y el teseracto. El cuadrado es un objeto de 2 dimensiones, el cubo es un objeto de 3 dimensiones y el teseracto es un objeto de 4 dimensiones. Un objeto de 1 dimensión es sólo una línea. Se da una proyección del cubo ya que se ve en una pantalla bidimensional. Lo mismo ocurre con el teseracto, que además sólo puede mostrarse como una proyección incluso en un espacio tridimensional.
Otras dimensiones
En la ciencia moderna se utilizan otras dimensiones. Dimensiones como la temperatura y el peso pueden utilizarse para mostrar la posición de algo en espacios menos simples. Los científicos estudian esas dimensiones con el análisis dimensional.
Los matemáticos también utilizan las dimensiones. En matemáticas, las dimensiones son más generales. Las dimensiones en matemáticas pueden no medir cosas en el mundo. Las reglas para hacer aritmética con dimensiones en matemáticas podrían ser diferentes a las reglas aritméticas habituales.
Dimensiones y vectores
Los vectores se utilizan para mostrar distancias y direcciones. Los vectores se utilizan a menudo en la ingeniería y la ciencia, y a veces en las matemáticas.
Un vector es una lista de números. Hay un número por cada dimensión. Existen reglas aritméticas para los vectores.
Por ejemplo, si Jane quiere saber la posición de Sally, ésta puede dar a Jane un vector que muestre la posición. Si Jane y Sally están en el mundo, hay tres dimensiones. Por lo tanto, Sally le da a Jane una lista de tres números para mostrar su posición. Los tres números del vector que Sally le da a Jane pueden ser
- La distancia de Sally al norte de Jane
- La distancia de Sally al este de Jane
- La altura de Sally sobre Jane
Páginas relacionadas
- 3D
- Hipercubo, generalización del cuadrado y del cubo más allá de las tres dimensiones
- El espaciotiempo de Minkowski, una variedad de cuatro dimensiones
- Espacio-tiempo
Preguntas y respuestas
P: ¿Qué es una dimensión?
R: Una dimensión es una forma de medir, ver y experimentar el mundo utilizando conceptos como arriba y abajo, de derecha a izquierda, de atrás a adelante, caliente y frío, cuánto pesa y cuánto mide. También puede definirse como los grados de libertad o la forma en que un objeto puede moverse en un espacio concreto.
P: ¿Cómo definen los matemáticos el espacio euclidiano?
R: Los matemáticos definen el espacio euclidiano como algo especificado por tres dimensiones que suelen llamarse longitud, anchura y profundidad.
P: ¿Cuál es el número de vectores en un espacio vectorial?
R: El número de vectores de un espacio vectorial es igual a la cardinalidad (o número de vectores) de su conjunto base.
P: ¿Cuántas dimensiones se utilizan para medir la posición?
R: Para medir la posición se utilizan tres dimensiones (longitud, anchura y altura). En algunas ocasiones, se puede utilizar una cuarta dimensión (4D) -el tiempo- para mostrar la posición de un evento en el tiempo y el espacio.
P: ¿Qué significa dim(V)?
R: Dim(V) se refiere a la dimensión de V, que es igual a la cardinalidad (o número de vectores) de su conjunto base o igual al número de direcciones de líneas rectas que tiene.
P: ¿Existe una definición que satisfaga todos los conceptos relacionados con las dimensiones?
R: No, no existe una única definición que pueda satisfacer todos los conceptos relacionados con las dimensiones.
Buscar dentro de la enciclopedia