Espaciotiempo de Minkowski: definición y métrica en relatividad

Descubre el espaciotiempo de Minkowski: definición, métrica (-+++), propiedades y su papel clave en la relatividad especial explicado con claridad.

Autor: Leandro Alegsa

En la relatividad especial, el espaciotiempo de Minkowski es una variedad de cuatro dimensiones, creada por Hermann Minkowski. Tiene cuatro dimensiones: tres dimensiones del espacio (x, y, z) y una dimensión del tiempo. El espaciotiempo de Minkowski tiene una firma métrica de (-+++), y describe una superficie plana cuando no hay masa. La convención en este artículo es llamar al espaciotiempo de Minkowski simplemente espaciotiempo.

Sin embargo, el espaciotiempo de Minkowski sólo se aplica en la relatividad especial. La relatividad general utilizó la noción de espaciotiempo curvo para describir los efectos de la gravedad y el movimiento acelerado.

Definición métrica y elemento de línea

El espaciotiempo de Minkowski se equipara con un espacio vectorial de cuatro dimensiones sobre el que existe un producto interior no degenerado de tipo Lorentz. En coordenadas naturales (ct, x, y, z) el elemento de línea o intervalo infinitesimal se escribe

ds² = ημν dxμ dxν = −c² dt² + dx² + dy² + dz²,

donde ημν = diag(−1, +1, +1, +1) es el tensor métrico de Minkowski según la convención (-+++). Muchos autores usan la convención opuesta (+−−−); ambas son equivalentes salvo el signo global y se debe indicar la convención empleada. Si se trabaja en unidades relativistas con c = 1, la expresión se simplifica a ds² = −dt² + dx² + dy² + dz².

Estructura causal y clasificación de intervalos

El signo del intervalo ds² determina la relación causal entre dos eventos:

  • Intervalo timelike (ds² < 0): existe una trayectoria con velocidad menor que c que conecta los eventos. Se puede definir un tiempo propio τ por ds² = −c² dτ², y τ es el tiempo medido por un reloj que sigue esa trayectoria.
  • Intervalo lightlike o nulo (ds² = 0): sólo puede conectarlos una señal que viaje exactamente a la velocidad de la luz (luz o partículas sin masa).
  • Intervalo spacelike (ds² > 0): no existe señal causal entre los eventos; su orden temporal puede depender del sistema de referencia.

Geométricamente, estos tres tipos están organizados por el cono de luz en cada punto: las direcciones timelike están dentro del cono de luz, las lightlike sobre el cono y las spacelike fuera del cono.

Simetrías: transformaciones de Lorentz y grupo de Poincaré

El espaciotiempo de Minkowski es homogéneo y anisótropo en el sentido de que su métrica es la misma en todos los puntos y direcciones. Las transformaciones que dejan invariante la métrica ημν son las transformaciones de Lorentz (rotaciones y boosts) y las traslaciones en el tiempo y en el espacio. El conjunto de todas ellas forma el grupo de Poincaré, que encierra la simetría fundamental de la relatividad especial. La invariancia del intervalo ds² bajo transformaciones de Lorentz es la base matemática de la constancia de la velocidad de la luz y de la relatividad de la simultaneidad.

Propiedades geométricas y físicas

  • El espaciotiempo de Minkowski es plano: su tensor de curvatura de Riemann es nulo. Esto refleja la ausencia de gravedad (o masa-energía local) en la escala considerada.
  • Las geodésicas en este espaciotiempo son líneas rectas en coordenadas inerciales; representan el movimiento de partículas libres (no sometidas a fuerzas) en relatividad especial.
  • El producto interior de Minkowski define una "norma" Lorentziana que no es positiva definida; por ello se habla de la métrica de tipo Lorentz en vez de Riemanniana propia de la geometría euclídea.

Usos y aplicaciones

El espaciotiempo de Minkowski es la arena matemática donde se formulan las leyes de la física relativista sin gravedad: electrodinámica clásica y cuántica, mecánica relativista, teoría de campos en espacio plano y análisis de procesos de partículas en colisionadores. Sirve además como el límite local en torno a cualquier punto de un espaciotiempo curvo de la relatividad general (principio de equivalencia): localmente y para observadores suficientemente pequeños, la geometría se aproxima a la de Minkowski.

Notas sobre convenciones

Cuando se lea literatura sobre relatividad conviene comprobar la convención de signos de la métrica y la normalización de las coordenadas temporales (si se usa t o ct). La elección (-+++) empleada aquí es común en buena parte de la física de partículas y en varios textos de relatividad especial.

En resumen, el espaciotiempo de Minkowski es el modelo geométrico plano y Lorentziano que captura la estructura causal y la simetría de la relatividad especial, sirviendo de punto de partida para la descripción de fenómenos relativistas en ausencia de efectos gravitacionales.


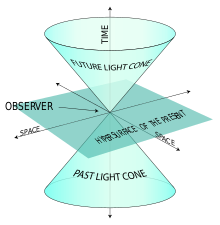
  Ejemplo de un cono de luz.  Zoom
Ejemplo de un cono de luz.  

Definición(es)

Matemáticas

El espaciotiempo puede considerarse como un sistema de coordenadas de cuatro dimensiones en el que los ejes vienen dados por

( c t , x , y , z ) {\displaystyle (ct,x,y,z)} {\displaystyle (ct,x,y,z)}

También se pueden denotar por

( x 1 , x 2 , x 3 , x 4 ) {\displaystyle (x_{1},x_{2},x_{3},x_{4})} {\displaystyle (x_{1},x_{2},x_{3},x_{4})}

{\displaystyle x_{1}}Donde x 1 {\displaystyle x_{1}} representa c t {\displaystyle ct}{\displaystyle ct} . La razón para medir el tiempo en unidades de la velocidad de la luz por la coordenada temporal es que las unidades para el tiempo son las mismas que las unidades para el espacio. El espacio-tiempo tiene la diferencial para la longitud de arco dada por

d s 2 = - c 2 d t 2 + d x 2 + d y 2 + d z 2 {\displaystyle ds^{2}=-c^{2}dt^{2}+dx^{2}+dy^{2}+dz^{2}} {\displaystyle ds^{2}=-c^{2}dt^{2}+dx^{2}+dy^{2}+dz^{2}}

Esto implica que el espaciotiempo tiene un tensor métrico dado por

g u v = [ - 1 0 0 0 1 0 0 0 1 0 0 0 1 ] {\displaystyle g_{uv}={begin{bmatrix}-1&0&0&0\0&1&0\0&0&1{end{bmatrix}} {\displaystyle g_{uv}={\begin{bmatrix}-1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{bmatrix}}}

Como ya se ha dicho, el espacio-tiempo es plano en todas partes; hasta cierto punto, se puede pensar en él como un plano.

Simple

El espaciotiempo puede considerarse como el "escenario" en el que se desarrollan todos los acontecimientos del universo. Todo lo que se necesita para especificar un punto en el espaciotiempo es un tiempo determinado y una orientación espacial típica. Es difícil (prácticamente imposible) visualizar las cuatro dimensiones, pero se puede hacer alguna analogía, utilizando el método siguiente.



 

Diagramas del espacio-tiempo

Hermann Minkowski introdujo un determinado método para graficar los sistemas de coordenadas en el espaciotiempo de Minkowski. Como se ve a la derecha, diferentes sistemas de coordenadas discreparán sobre la orientación espacial de un objeto y/o su posición en el tiempo. Como puede ver en el diagrama, sólo hay un eje espacial (el eje x) y un eje temporal (el eje c). Si es necesario, se puede introducir una dimensión espacial adicional, (el eje y); por desgracia, éste es el límite del número de dimensiones: graficar en cuatro dimensiones es imposible. La regla para graficar en el espaciotiempo de Minkowski es la siguiente:

1) El ángulo entre el eje x y el eje x'viene dado por t a n ( α ) = v c {\displaystyle tan(\alpha )={\frac {v}{c}}{\displaystyle tan(\alpha )={\frac {v}{c}}} donde v es la velocidad del objeto

2) La velocidad de la luz a través del espaciotiempo siempre forma un ángulo de 45 grados con cualquier eje.



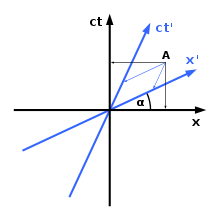
 En la teoría de la relatividad, ambos observadores asignan el evento en A a tiempos diferentes.  Zoom
En la teoría de la relatividad, ambos observadores asignan el evento en A a tiempos diferentes.  

El espacio-tiempo en la relatividad general

En la teoría general de la relatividad, Einstein utilizó la ecuación

G m v = 8 π G T m v {\displaystyle \mathbb {G} _{mv}=8\i {\mathcal {G}{mathbb {T}} mv}} {\displaystyle \mathbb {G} _{mv}=8\pi {\mathcal {G}}\mathbb {T} _{mv}}

Para permitir que el espacio-tiempo se curve realmente; los efectos resultantes son los de la gravedad.



 

Páginas relacionadas

Control de la autoridad: Bibliotecas nacionales Edit this at Wikidata
  • Francia (datos)
  • Alemania
  • Estados Unidos
  • Letonia
  • República Checa


 

Preguntas y respuestas

P: ¿Qué es el espaciotiempo de Minkowski?


R: El espaciotiempo de Minkowski es un colector de cuatro dimensiones creado por Hermann Minkowski. Tiene tres dimensiones de espacio (x, y, z) y una dimensión de tiempo.

P: ¿Cuál es la firma métrica del espaciotiempo de Minkowski?


R: La firma métrica del espaciotiempo de Minkowski es (-+++).

P: ¿Cómo describe el espaciotiempo de Minkowski una superficie plana?


R: Cuando no hay masa, el espaciotiempo de Minkowski describe una superficie plana.

P: ¿Se aplica el espaciotiempo de Minkowski a la relatividad general?


R: No, el espaciotiempo de Minkowski sólo se aplica en la relatividad especial. La relatividad general utiliza la noción de espaciotiempo curvo para describir los efectos de la gravedad y el movimiento acelerado.

P: ¿Cuántas dimensiones tiene el espaciotiempo de Minkowski?


R: El espaciotiempo Minkowsi tiene cuatro dimensiones: tres dimensiones del espacio (x, y, z) y una dimensión del tiempo.

P: ¿Quién creó el concepto de Espaciotiempo Minkowsi?


R: Hermann Minkowksi creó el concepto de Espaciotiempo MInkowski.


Buscar dentro de la enciclopedia
AlegsaOnline.com - 2020 / 2025 - License CC3