Distribución de Gumbel: definición en estadística y aplicaciones en extremos
Distribución de Gumbel: guía práctica sobre definición, modelado de valores extremos y aplicaciones en la predicción de inundaciones, terremotos y riesgos extremos.
La distribución de Gumbel es una distribución deprobabilidad de valores extremos.
En la teoría de la probabilidad y la estadística, la distribución de Gumbel se utiliza para modelar la distribución del máximo (o el mínimo) de un número de muestras de diversas distribuciones.
Una distribución de este tipo podría utilizarse para representar la distribución del nivel máximo de un río en un año concreto si se dispusiera de una lista de valores máximos de los últimos diez años. También es útil para predecir la probabilidad de que se produzca un terremoto extremo, una inundación u otra catástrofe natural.
Definición y fórmulas básicas
La forma más común de la distribución de Gumbel (para máximos) tiene dos parámetros: μ (ubicación) y β > 0 (escala). Sus funciones son:
- Función de distribución acumulada (CDF): F(x) = exp(-exp(-(x - μ)/β)).
- Densidad de probabilidad (PDF): f(x) = (1/β) · exp(-z - exp(-z)), donde z = (x - μ)/β.
La forma estandarizada (μ = 0, β = 1) se conoce como la Gumbel estándar.
Propiedades importantes
- Media: E[X] = μ + γ β, donde γ ≈ 0.5772156649 es la constante de Euler–Mascheroni.
- Varianza: Var(X) = (π² / 6) β².
- Asimetría (skewness): ≈ 1.139547 (valor positivo, cola derecha más pesada que la izquierda en sentido relativo).
- Curtosis en exceso: ≈ 2.4 (cola más pesada que la normal, pero no tan pesada como distribuciones con cola algebraica).
- Comportamiento de cola: la cola derecha decrece exponencialmente; por tanto, no es adecuada para modelar fenómenos con colas muy pesadas (colas algebraicas).
Relación con otras distribuciones y teoría de extremos
- La distribución de Gumbel es uno de los tres tipos límites en la teoría de valores extremos y corresponde al caso con parámetro de forma ξ = 0 de la distribución generalizada de valores extremos (GEV). Es el llamado tipo I de Fisher–Tippett.
- La Gumbel para mínimos se obtiene cambiando de signo la variable: si X tiene Gumbel para máximos, entonces -X tiene Gumbel para mínimos (o aplicando la transformación adecuada en la CDF).
- Se relaciona con la distribución doble exponencial (o Laplace) en ciertas transformaciones, pero no son idénticas.
Estimación y ajuste a datos
Para ajustar una distribución de Gumbel a datos se usan métodos como:
- Máxima verosimilitud (MLE): método habitual y eficiente para muestras moderadas/grandes.
- Método de los momentos: utiliza media y varianza muestrales para obtener μ y β aproximados.
- L-momentos: recomendadas en hidrología y análisis de extremos por su robustez frente a valores atípicos y su buen comportamiento en muestras pequeñas.
Para evaluar la bondad de ajuste conviene usar gráficos Q–Q, pruebas como Anderson–Darling o Kolmogorov–Smirnov, y análisis de residuales. En fenómenos con colas pesadas, comparar con alternativas (p. ej. GEV con ξ ≠ 0, Pareto) es aconsejable.
Aplicaciones prácticas
- Hidrología: cálculo de caudales máximos, niveles de crecida, diseño de diques y presas.
- Meteorología y climatología: velocidades máximas del viento, precipitaciones extremas, temperaturas máximas.
- Ingeniería: resistencia máxima de materiales, cargas extremas, seguridad estructural frente a eventos raros.
- Gestión de riesgos y seguros: estimación de pérdidas máximas en horizontes temporales determinados (aunque en finanzas suele preferirse modelos con colas más pesadas).
- Otras ciencias: sismología (al estudiar la distribución de magnitudes máximas en ventanas temporales), oceanografía (altura máxima de olas), etc.
Cómo simular datos Gumbel
Si U es una variable uniforme en (0,1), una simulación de Gumbel se obtiene por la transformación inversa:
X = μ - β · ln(-ln(U)).
Limitaciones y consideraciones
- La Gumbel asume que la cola del máximo tiene decaimiento de tipo exponencial; no sirve bien cuando los datos muestran colas pesadas (colas algebraicas).
- El tamaño de muestra y la independencia de las observaciones (o al menos el tratamiento de dependencia temporal) afectan la estimación y las inferencias.
- En la práctica conviene comparar varios modelos de valores extremos (p. ej. GEV con ξ estimado) y realizar análisis de sensibilidad a la elección del umbral o al periodo de retorno.
Ejemplo ilustrativo
Si se ajusta una Gumbel con parámetros μ = 10 y β = 2 para modelar niveles máximos anuales, la probabilidad de que el nivel supere 16 en un año es:
P(X > 16) = 1 - F(16) = 1 - exp(-exp(-(16 - 10)/2)) ≈ 1 - exp(-exp(-3)) ≈ 1 - exp(-0.0498) ≈ 0.0487 (≈ 4.9%).
En resumen, la distribución de Gumbel es una herramienta central en el análisis de valores extremos, muy útil para estimar probabilidades y periodos de retorno de eventos raros cuando la cola se comporta de forma exponencial. Su uso requiere comprobar suposiciones, comparar modelos y aplicar métodos de estimación adecuados al tamaño y características de los datos.
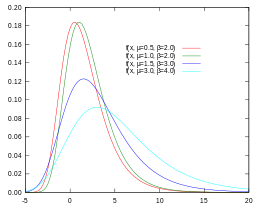
Función de distribución de probabilidad de Gumbel (PDF)
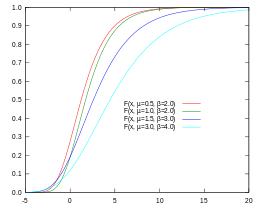
Función de distribución acumulativa de Gumbel (CDF)
Propiedades
La distribución de Gumbel es una distribución de probabilidad continua. Las distribuciones de Gumbel son una familia de distribuciones con la misma forma general. Estas distribuciones se diferencian por sus parámetros de localización y escala: la media ("promedio") de la distribución define su localización, y la desviación estándar ("variabilidad") define la escala.
Se reconoce la función de densidad de probabilidad de Gumbel (PDF) y la función de distribución acumulativa de Gumbel (CDF).
En la PDF, la probabilidad P de que un valor V ocurra entre los límites A y B, brevemente escrita como P(A<V<B), se encuentra por el área bajo la curva de la PDF entre A y B.
| Ejemplo de probabilidad en el PDF |
| En la figura de la función de densidad de probabilidad normal, los valores del eje horizontal deben ser: μ-3σ, μ-2σ, μ-1σ, μ+1σ, μ+2σ y μ+3σ respectivamente. μ = media, σ = desviación estándar. |
A diferencia de la distribución normal, la PDF de Gumbel es a-simétrica y se inclina hacia la derecha.
CDF
En la FCD, la probabilidad de que un valor V sea menor que A se encuentra directamente como el valor de la FCD en A:
P ( V ≤ A ) = C D F ( A ) {\displaystyle P(V\leq A)=CDF(A)} 
| Ejemplo de probabilidad en la FCD |
| En la figura de la CDF de Gumbel, la curva roja indica que la probabilidad de que V sea inferior a 5 es de 0,9 (o del 90%), mientras que para la línea azul oscuro esta probabilidad es de 0,7 o del 70% |

La función de densidad de probabilidad (PDF) normal es simétrica.
Matemáticas
El FCD
La expresión matemática de la FCD es:
C D F ( A ) = e - e - ( A - μ ) / β , {\displaystyle CDF(A)=e^{-e^{-(A-\mu )/\beta },}
donde μ es la moda (el valor donde la función de densidad de probabilidad alcanza su pico), e es una constante matemática, aproximadamente 2,718, y β es un valor relacionado con la desviación estándar (σ) :
β = σ 6 / π , {\displaystyle \beta =\sigma {\sqrt {6}}/\pi ,}
donde π es el símbolo griego de Pi, cuyo valor se aproxima a 22/7 o 3,142, y el símbolo {\displaystyle {\sqrt {\}} 
Modo y mediana
La moda μ se puede encontrar a partir de la mediana M, siendo el valor de A donde CDF(A)=0,5, y β:
μ = M + β ln ( ln 2 ) , {\displaystyle \mu =M+\beta \ln \left(\ln 2\right),}
donde ln es el logaritmo natural.
Media
La media, E(x), dada por:
E ( x ) = μ + c β , {\desde el punto de vista del operador {E} (x)=mu +c\beta ,} (x)=\mu +c\beta ,}
donde c {\displaystyle c}

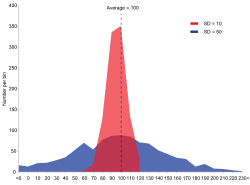
Hay dos series de datos: la roja y la azul. Ambas tienen la misma media (promedio) : 100, pero el grupo azul tiene una desviación estándar mayor (SD=σ=50) que el grupo rojo (SD=σ=10).
Estimación
En una serie de datos, los parámetros moda (μ) y β pueden estimarse a partir de la media, la mediana y la desviación estándar. El cálculo de las tres últimas magnitudes se explica en las respectivas páginas de la Wiki. Luego, con la ayuda de las fórmulas dadas en la sección anterior, se pueden calcular los factores μ y β. De esta manera, se puede determinar la FCD de la distribución de Gumbel que pertenece a los datos y encontrar la probabilidad de los valores de datos interesantes.

Distribución acumulativa de Gumbel ajustada a las precipitaciones máximas de un día de octubre utilizando CumFreq
Aplicación
En hidrología, la distribución de Gumbel se utiliza para analizar variables como los valores máximos mensuales y anuales de las precipitaciones diarias y los volúmenes de descarga de los ríos, y también para describir las sequías.
La imagen azul ilustra un ejemplo de ajuste de la distribución de Gumbel a las precipitaciones máximas de un día de octubre, mostrando también el cinturón de confianza del 90% basado en la distribución binomial.
Preguntas y respuestas
P: ¿Qué es la distribución de Gumbel?
R: La distribución de Gumbel es una distribución de probabilidad de valores extremos.
P: ¿Para qué se utiliza la distribución de Gumbel?
R: La distribución de Gumbel se utiliza para modelar la distribución del máximo (o el mínimo) de un número de muestras de varias distribuciones.
P: ¿Cómo puede utilizarse la distribución de Gumbel para predecir catástrofes naturales?
R: La distribución de Gumbel es útil para predecir la probabilidad de que se produzca un terremoto extremo, una inundación u otra catástrofe natural.
P: ¿Cuál es un ejemplo de uso de la distribución de Gumbel para representar un acontecimiento pasado?
R: La distribución de Gumbel podría utilizarse para representar la distribución del nivel máximo de un río en un año concreto si existiera una lista de valores máximos de los últimos diez años.
P: ¿La distribución de Gumbel sólo es útil para predecir catástrofes naturales?
R: No, la distribución de Gumbel puede utilizarse para modelizar la distribución de valores extremos en cualquier situación.
P: ¿Puede utilizarse la distribución de Gumbel para modelizar el valor mínimo de un conjunto de muestras?
R: Sí, la distribución de Gumbel puede utilizarse para modelar la distribución del máximo o del mínimo de un conjunto de muestras.
P: ¿Es la distribución de Gumbel una distribución comúnmente utilizada en teoría de la probabilidad y estadística?
R: Sí, la distribución de Gumbel es una distribución de uso común en la teoría de la probabilidad y la estadística, especialmente para modelar valores extremos.
Buscar dentro de la enciclopedia



