Impedancia eléctrica: definición, fórmulas y ejemplos prácticos
Impedancia eléctrica: definición clara, fórmulas esenciales y ejemplos prácticos para comprender resistencias, inductores y condensadores según la frecuencia.
Definición y concepto básico
La impedancia eléctrica es la cantidad de oposición que presenta un circuito al cambio de corriente o tensión. Es una generalización de la resistencia para señales variables en el tiempo (AC) y se expresa mediante números complejos para incluir tanto la parte que disipa energía como la que almacena y devuelve energía.
Formas de expresar la impedancia
Las dos formas principales de escribir una impedancia son (ver el plano de impedancia complejo):
- Con la resistencia "R" (la parte real) y la reactancia "X" (la parte imaginaria), por ejemplo Z = R + jX. Un caso concreto: Z = 1 + 1 j {\displaystyle Z=1+1j}
. Aquí R = 1 Ω y X = 1 Ω. - Con magnitud y fase: la magnitud | Z | {\displaystyle \left\vert Z\right\vert }
y el ángulo θ {\displaystyle \angle \theta } 
). Por ejemplo: Z = 1,4 ∠ 45 ∘ {\displaystyle Z=1,4\angle 45^{\circ }} 
(1,4 ohmios a 45 grados).
Conversión entre formas:
- Magnitud: |Z| = sqrt(R² + X²).
- Ángulo: θ = arctan(X / R) (en radianes o grados según convenga).
Relación con la resistencia (CA vs CC)
La resistencia es un caso particular de impedancia que no depende de la frecuencia: un resistor resiste la corriente independientemente de la velocidad de cambio. La ley de Ohm para resistencias es
V = R ∗ I {\displaystyle V=R*I}
, donde V es la tensión, R la resistencia e I la corriente.
Para señales alternas la ley equivalente usa la impedancia compleja Z:
V = Z ∗ I {\displaystyle V=Z*I}
.
Impedancia de los elementos pasivos
La impedancia depende de la frecuencia. Un inductor opone más a cambios rápidos de corriente y un condensador opone más a cambios rápidos de tensión. Las expresiones son:
Para el inductor: Z = j 2 π f L {\displaystyle Z=j2\pi fL\,} 
.
Para el condensador: Z = 1 j 2 π f C {\displaystyle Z={\frac {1}{j2\pi fC}}} 
.
En estas fórmulas Z es la impedancia, j el número imaginario - 1 {\displaystyle {\sqrt {-1}} 
, π 
es la constante pi, f la frecuencia, L la inductancia y C la capacitancia. Las unidades son ohmios: ohmio (Ω) 
.
Signo de la reactancia y convención
- Reactancia inductiva: XL = ωL = 2πfL (se representa como +jXL).
- Reactancia capacitiva: XC = 1/(ωC) y la impedancia del condensador es ZC = 1/(jωC) = −jXC (reactancia negativa en el eje imaginario).
Ejemplos prácticos
Ejemplo 1 — Conversión rectangular a polar:
- Dado Z = 1 + j1 (R = 1 Ω, X = 1 Ω):
- Magnitud: |Z| = sqrt(1² + 1²) = sqrt(2) ≈ 1,414 Ω.
- Ángulo: θ = arctan(1/1) = 45°.
- Por tanto Z ≈ 1,414 ∠ 45° (como en el ejemplo gráfico: Z = 1,4 ∠ 45 ).
Ejemplo 2 — Impedancias a 50 Hz:
- Inductor: L = 10 mH = 0,01 H → XL = 2π·50·0,01 ≈ 3,14 Ω → ZL = j3,14 Ω.
- Condensador: C = 100 nF = 100·10⁻⁹ F → XC = 1/(2π·50·100·10⁻⁹) ≈ 31.830 Ω → ZC = −j31.830 Ω (muy alta a baja frecuencia).
Energía, potencia y comportamiento físico
De forma simplificada:
- La resistencia disipa energía en forma de calor (potencia activa P).
- La reactancia (inductores y condensadores) almacena energía en campos magnéticos o eléctricos y puede devolverla a la fuente (potencia reactiva Q, sin consumo neto sobre un ciclo).
- La potencia compleja: S = P + jQ = V·I*, donde I* es el conjugado complejo de la corriente.
Coincidencia de impedancias y reflexiones
Si la impedancia de la fuente, el cable y la carga no son iguales, una parte de la señal se refleja en la unión, desperdiciando energía y provocando interferencias. El coeficiente de reflexión se calcula con:
Γ = Z L - Z S Z L + Z S {\displaystyle \Gamma ={Z_{L}-Z_{S}{sobre Z_{L}+Z_{S}}
donde Γ {\displaystyle \Gamma } 
(gamma mayúscula) es el coeficiente de reflexión, Z S {\displaystyle Z_{S}} 
es la impedancia de la fuente y Z L {\displaystyle Z_{L}} 
la de la carga.
Si ZL = ZS entonces Γ = 0 (coincidencia perfecta, sin reflexiones). Este concepto es clave en líneas de transmisión y RF.
Impedancia de onda y ejemplos adicionales
Cualquier medio que soporte ondas tiene una impedancia de onda. Por ejemplo, el espacio libre tiene una impedancia característica aproximada de 377 Ω {displaystyle \Omega } .
Resumen y recomendaciones prácticas
- La impedancia combina efecto resistivo (disipación) y reactivo (almacenamiento) y depende de la frecuencia.
- Para analizar circuitos en AC use representación compleja (R + jX) o fasores (|Z| ∠ θ).
- En diseño y medida: controle la coincidencia de impedancias para evitar pérdidas y reflexiones, especialmente en RF y transmisión de señales.
- Herramientas útiles: medidas con analizador de redes, cálculo de fasores y transformada de Fourier para señales no sinusoidales.
Si desea, puedo añadir más ejemplos resueltos paso a paso (serie/paralelo RLC, cálculo de potencia, curvas de frecuencia) o preparar una hoja de cálculo para calcular impedancias según valores y frecuencia.
Una representación gráfica del plano de la impedancia compleja
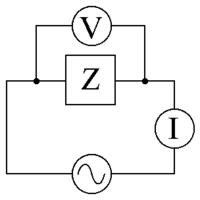
Una alimentación de CA que aplica una tensión V {\displaystyle \scriptstyle V} 
a través de una impedancia Z {\displaystyle \scriptstyle Z} , conduciendo una corriente I {\displaystyle \scriptstyle I} . 
que impulsa una corriente I {\displaystyle \scriptstyle I} 
.
Una señal se refleja parcialmente donde la impedancia cambia.
Fase
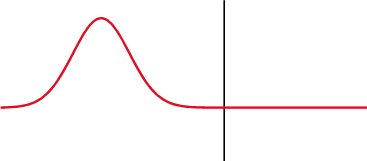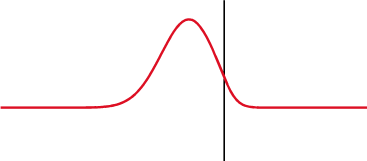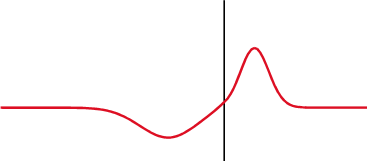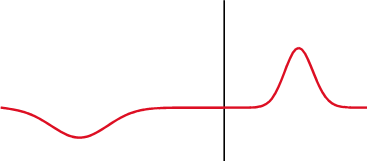
A través de una resistencia, tanto la tensión como la corriente suben y bajan al mismo tiempo, se dice que están en fase, pero con una impedancia es diferente, la tensión se desplaza 1/4 de longitud de onda por detrás de la corriente en un condensador, y por delante en un inductor.
Un 1/4 de longitud de onda se suele representar con el número imaginario "j", que también equivale a un desplazamiento de 90 grados.
El uso del número imaginario "j" simplifica mucho las matemáticas, permite calcular la impedancia total de la misma manera que se hace con las resistencias, por ejemplo una resistencia más una impedancia en serie es R+Z, y en paralelo es (R*Z)/(R+Z).
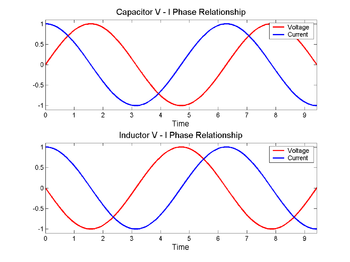
A través de un condensador (arriba), la tensión (rojo) cambia después de la corriente (azul), a través de un inductor (abajo) es antes. La diferencia de fase entre la tensión y la corriente es de 1/4 de longitud de onda.
Preguntas y respuestas
P: ¿Qué es la impedancia eléctrica?
R: La impedancia eléctrica es la cantidad de oposición que presenta un circuito al cambio de corriente o tensión.
P: ¿Cómo se puede escribir la impedancia eléctrica?
R: La impedancia eléctrica puede escribirse con la resistencia "R" (parte real) y la reactancia "X" (parte imaginaria), así como con una magnitud, fase, tamaño y ángulo.
P: ¿Cuál es la diferencia entre resistencia e impedancia?
R: La diferencia clave entre resistencia e impedancia es la palabra "cambio"; en otras palabras, la velocidad de cambio afecta a la impedancia. La resistencia resiste cualquier corriente que pase a través de ella, mientras que un inductor resiste los cambios en la corriente y un condensador resiste los cambios en la tensión.
P: ¿Cuáles son algunas fórmulas asociadas a la resistencia y la impedancia?
R: Para la resistencia, V=R*I donde V es la tensión, R es la resistencia e I es la corriente; para los inductores Z=j2πfL; para los condensadores Z=1/j2πfC; donde Z representa la impedancia, j representa el número imaginario -1 , π representa la constante pi, f representa la frecuencia, L representa la inductancia, C representa la capacitancia.
P: ¿Cuáles son algunas explicaciones físicas de la resistencia frente a la impedancia?
R: La resistencia está causada por los electrones que chocan con los átomos en el interior de las resistencias, mientras que la impedancia de un inductor procede de la creación de un campo eléctrico y la de un condensador de la creación de un campo magnético. Además, las resistencias disipan energía mientras que los inductores y los condensadores almacenan energía que puede ser devuelta a la fuente cuando ésta baja.
P: ¿Cómo se calcula el coeficiente de reflexión?
R: El coeficiente de reflexión puede calcularse utilizando Γ=(ZL-ZS)/(ZL+ZS) donde Γ (gamma mayúscula) representa el coeficiente de reflexión; ZS representa la impedancia de la fuente; ZL representa la impedancia de la carga
Buscar dentro de la enciclopedia