Geometría y topología del Universo: evidencia y modelos
Explora la geometría y topología del universo: evidencia observacional, curvatura, modelos FLRW y debate sobre si el cosmos es plano o tiene topología global.
La forma del Universo no puede discutirse con términos cotidianos, porque todos los términos tienen que ser los de la relatividad einsteiniana. La geometría del universo no es, pues, la geometría euclidiana ordinaria de nuestra vida cotidiana.
Según la teoría especial de la relatividad, es imposible decir si dos acontecimientos distintos ocurren al mismo tiempo si esos acontecimientos están separados en el espacio. Hablar de "la forma del universo (en un punto del tiempo)" es ingenuo desde el punto de vista de la relatividad especial. Debido a la relatividad de la simultaneidad, no podemos hablar de puntos diferentes en el espacio como si estuvieran "en el mismo punto del tiempo" ni, por tanto, de "la forma del universo en un punto del tiempo".
Lo que hacen los astrofísicos es preguntarse si un determinado modelo del universo es coherente con lo que se conoce a través de las observaciones y mediciones del universo. Si el universo observable es más pequeño que todo el universo (en algunos modelos es muchos órdenes de magnitud más pequeño o incluso infinitesimal), la observación se limita a una parte del todo.
La consideración de la forma del universo puede dividirse en dos:
- la geometría local, que se refiere especialmente a la curvatura del universo, sobre todo en el universo observable, y
- la geometría global, que se refiere a la topología del universo en su conjunto, cuya medición puede no ser posible.
El universo observable es la base para probar cualquier modelo del universo. Es un volumen esférico (una bola) centrado en el observador, independientemente de la forma del universo en su conjunto. Cada lugar del universo tiene su propio universo observable, que puede coincidir o no con el centrado en la Tierra.
Las mediciones recientes han llevado a la NASA a afirmar que "ahora sabemos que el universo es plano con sólo un 0,4% de margen de error". Dentro de un modelo, el modelo FLRW, la forma actual más popular del Universo que se ajusta a los datos observacionales es el modelo plano infinito. Hay otros modelos que también se ajustan a los datos.
Relatividad, tiempo cósmico y la noción de "forma"
Aunque la teoría especial de la relatividad invalida una simultaneidad absoluta entre observadores en movimiento relativo, en cosmología se utiliza una noción práctica de tiempo compartido llamada tiempo cósmico. Este tiempo está definido por observadores comóviles (los que se mueven con la expansión media del universo) y por la existencia de un marco preferente: el marco en el que la radiación de fondo de microondas (CMB) está, en promedio, isotrópica. Gracias a esa foliación de la variedad espacio‑temporal en "hiperficies de tiempo cósmico" sí resulta útil y coherente hablar de la geometría espacial en un instante cósmico dado.
Geometría local: curvatura espacial y parámetros cosmológicos
La curvatura espacial describe cómo se comporta la geometría en vecindades pequeñas comparadas con la escala del universo observable. En los modelos homogéneos e isotrópicos de Friedmann–Lemaître–Robertson–Walker (FLRW) la curvatura espacial puede ser positiva (esfera 3D), cero (plana euclidiana 3D) o negativa (silla de montar 3D). Matemáticamente se codifica mediante un parámetro de curvatura y, en la práctica observacional, mediante la suma de las densidades relativas normalizadas (parámetro de densidad total Ω_tot):
- Ω_tot = 1 corresponde a un universo espacialmente plano.
- Ω_tot > 1 indica curvatura positiva (universo cerrado, recorrido finito en ciertas topologías).
- Ω_tot < 1 indica curvatura negativa (universo abierto).
Los experimentos y análisis cosmológicos actuales (CMB, oscilaciones acústicas bariónicas, supernovas tipo Ia, lente gravitatoria y estructura a gran escala) restringen Ω_tot con alta precisión. En términos prácticos, los resultados combinados de misiones como WMAP y Planck junto con otras sondas limitan la curvatura espacial a fracciones de por ciento: el universo es compatible con plano dentro de márgenes muy pequeños, aunque el límite exacto depende del conjunto de datos y supuestos del análisis.
Topología global: finito o infinito, conexo o multiplemente conectado
La topología del universo es independiente de la curvatura local. Existe la posibilidad de tener un universo con curvatura nula y, sin embargo, de tamaño finito si su espacio es compacto (por ejemplo, un toro tridimensional), o un universo con curvatura positiva y distintas topologías posibles (por ejemplo la esfera 3 o el espacio dodecaédrico de Poincaré). En otras palabras, plano no implica necesariamente infinito.
Detectar una topología no trivial requeriría señales observables como patrones repetidos en la distribución de galaxias, repeticiones de objetos extragalácticos o círculos coincidentes en el cielo del CMB (las llamadas "matched circles"). Si la escala de la topología es mayor que el horizonte observable, dichas características estarían fuera de nuestro alcance y, por tanto, la topología global quedaría indetectable con observaciones actuales.
Evidencia observacional y métodos
Las principales herramientas para inferir la geometría del universo son:
- Radiación cósmica de fondo (CMB): el ángulo aparente del horizonte acústico en el CMB (posiciones de los picos acústicos en el espectro angular) es muy sensible a la curvatura espacial.
- Oscilaciones acústicas bariónicas (BAO): proporcionan una "regla estándar" en la distribución de galaxias que ayuda a medir distancias cosmológicas y, por ende, la geometría.
- Supernovas tipo Ia: sirven como indicadores de distancia (candles estándar) que combinados con BAO y CMB restringen la historia de la expansión y la curvatura.
- Lente gravitatoria y clustering: las distorsiones por lente y la distribución de la materia oscura completan las restricciones sobre los parámetros cosmológicos.
Combinando estas mediciones se reduce la degeneración entre parámetros —por ejemplo entre densidad de materia, energía oscura y curvatura— y se obtienen límites cada vez más estrictos a la curvatura espacial.
Modelos cosmológicos y su consistencia con los datos
El modelo estándar en cosmología es el modelo ΛCDM dentro de la familia FLRW: supone homogeneidad e isotropía a gran escala, materia oscura fría y energía oscura representada por una constante cosmológica Λ. La inflación cósmica, un episodio de expansión exponencial en el universo primitivo, ofrece una explicación teórica de por qué observamos una curvatura espacial tan cercana a cero: la inflación estira cualquier curvatura inicial hasta dejarla prácticamente plana en la escala observable.
Sin embargo, otras posibilidades siguen abiertas en los márgenes de incertidumbre: universos ligeramente cerrados o abiertos, topologías compactas, o modelos anisótropos (como los modelos de Bianchi) han sido estudiados y comparados con los datos. Algunos análisis han investigado si anomalías en el CMB podrían indicar una topología o geometría distinta, pero hasta ahora no hay evidencia concluyente que imponga un cambio importante al modelo plano ΛCDM.
Conclusiones
En resumen:
- Hablar de la "forma del universo" exige un marco relativista: la noción operativa de forma se refiere a la geometría espacial en superficies de tiempo cósmico para observadores comóviles.
- La evidencia observacional acumulada indica que la curvatura espacial es extremadamente pequeña, compatible con un universo plano dentro de márgenes de fracciones de por ciento; los límites exactos dependen de los datos y supuestos del análisis.
- La topología global puede ser no trivial y permitir un universo finito aun siendo localmente plano; si su escala excede el horizonte observable, permanecerá indetectable.
- Finalmente, cualquier afirmación sobre la forma total del universo (más allá de la región observable) es necesariamente provisional y dependiente de modelos y de la precisión de nuestras observaciones futuras.
La cosmología continúa refinando estas medidas: nuevas observaciones (mejor resolución y sensibilidad en CMB, encuestas de galaxias más profundas, estudios de lentes débil y futuros proyectos como experimentos de siguiente generación) permitirán acotar aún más la geometría y explorar la posible topología del cosmos.
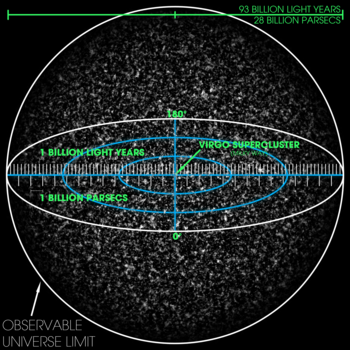
Visualización del universo tridimensional observable de 93.000 millones de años luz -o 28.000 millones de pársecs-. La escala es tal que los granos finos representan colecciones de un gran número de supercúmulos. El supercúmulo de Virgo - hogar de la Vía Láctea - está marcado en el centro, pero es demasiado pequeño para ser visto en la imagen.
Preguntas y respuestas
P: ¿Cuál es la forma del universo según las observaciones actuales?
R: Según mediciones recientes, la NASA ha afirmado que el universo es plano con sólo un margen de error del 0,4%.
P: ¿Cómo afecta la relatividad especial a nuestra comprensión de la forma del universo?
R: Debido a la relatividad de la simultaneidad, es imposible decir si dos acontecimientos distintos ocurren al mismo tiempo si dichos acontecimientos están separados en el espacio. Esto significa que no podemos hablar de puntos diferentes en el espacio como si estuvieran "en el mismo punto en el tiempo" ni, por tanto, de "la forma del universo en un punto en el tiempo".
P: ¿Qué tipo de geometría utilizan los astrofísicos cuando hablan de la forma del Universo?
R: Los astrofísicos utilizan la relatividad einsteiniana cuando discuten y prueban modelos para describir y predecir aspectos sobre el Universo. También tienen en cuenta la geometría local, relacionada especialmente con la curvatura, y la geometría global, relacionada con la topología.
P: ¿Cada lugar del Universo forma parte de un universo observable?
R: Sí, cada lugar del Universo tiene su propio universo observable que puede solaparse o no con uno centrado en la Tierra.
P: ¿Qué se entiende por "plano" cuando nos referimos a un modelo para describir/predicar aspectos sobre El Universo?
R: Dentro de un modelo, denominado FLRW (Friedmann-Lemaître-Robertson-Walker), 'plano' se refiere a un modelo infinitamente plano que se ha descubierto que se ajusta mejor a los datos observacionales. Significa que el espacio parece uniforme se mire por donde se mire y que en este modelo concreto no hay curvas ni dobleces.
P: ¿Existen otros modelos que se ajusten a los datos observacionales además del modelo plano infinito de FLRW?
R: Sí, existen otros modelos que también se ajustan a los datos observacionales además del modelo plano infinito de FLRW.
Buscar dentro de la enciclopedia