Álgebra elemental: definición, conceptos, ecuaciones y aplicaciones

Álgebra elemental: definición, conceptos y técnicas para resolver ecuaciones; aplicaciones prácticas en ciencias, negocios y construcción. Aprende paso a paso y mejora tu razonamiento.

Autor: Leandro Alegsa

30-03-2026 22:18

El álgebra elemental es la forma más básica de álgebra que se enseña a los estudiantes. Suele ser una de las siguientes áreas de las matemáticas que se enseñan a los estudiantes después de la aritmética. Mientras que en la aritmética sólo aparecen números y operadores como +, -, × y ÷, en el álgebra se utilizan variables (como a, x, y) para representar números. Esto es útil porque:

Permite resolver problemas sobre números "desconocidos". Esto significa aprender sobre ecuaciones y cómo resolverlas (por ejemplo, "encuentra un número x donde 3 x + 1 = 10 {\displaystyle 3x+1=10} $3x+1=10$ ").
Permite la generalización de las reglas de la aritmética. Mientras que algunos estudiantes entienden que 3 + 4 = 4 + 3 {\displaystyle 3+4=4+3} $3+4=4+3$ , ayuda a demostrar que a + b = b + a {\displaystyle a+b=b+a} para todas las a y b. Esto hace que el álgebra sea un buen paso para aprender sobre la abstracción (aprender ideas generales a partir de muchos ejemplos).
Ayuda a las personas a entender y crear relaciones funcionales (también llamadas a veces de causa y efecto). Un ejemplo de esto es "si se venden x entradas, el beneficio será de 3 x - 10 {\diseño 3x-10} $3x-10$ dólares".

Estas tres son las principales vertientes del álgebra elemental. El álgebra elemental se utiliza a menudo en muchas otras asignaturas, como las ciencias, los negocios y la construcción. El álgebra abstracta, un tema mucho más avanzado, suele enseñarse al final de la universidad.

Conceptos clave

Variables y expresiones: Una variable (por ejemplo, x o y) representa un número desconocido o que puede cambiar. Una expresión es una combinación de números, variables y operadores (por ejemplo, 2x + 5).
Ecuaciones: Una ecuación establece que dos expresiones son iguales (por ejemplo, 3x + 1 = 10). Resolver una ecuación significa encontrar el valor de la(s) variable(s) que hace(n) verdadera la igualdad.
Funciones: Una función relaciona una variable con otra: a cada valor de entrada le corresponde uno (o más) valores de salida. Por ejemplo, f(x) = 3x − 10 describe el beneficio según el número de entradas vendidas.
Polinomios: Expresiones formadas por sumas de monomios (por ejemplo, x^2 + 2x − 3). Trabajar con polinomios implica sumar, restar, multiplicar y factorizar.
Inecuaciones: Son desigualdades que involucran variables (por ejemplo, 2x + 3 > 7) y se resuelven considerando el signo de la desigualdad al operar con números negativos.

Propiedades fundamentales

El álgebra usa propiedades que permiten manipular expresiones con seguridad:

Conmutativa: a + b = b + a y a · b = b · a.
Asociativa: (a + b) + c = a + (b + c) y (ab)c = a(bc).
Distributiva: a(b + c) = ab + ac, útil para eliminar paréntesis y simplificar.

Cómo resolver ecuaciones simples (ejemplos)

Ejemplo lineal: resolver 3x + 1 = 10.

Restar 1 en ambos lados: 3x + 1 − 1 = 10 − 1 → 3x = 9.
Dividir entre 3: x = 9 / 3 → x = 3.
Verificar sustituyendo: 3·3 + 1 = 9 + 1 = 10, correcto.

Ejemplo cuadrático: resolver x^2 − 5x + 6 = 0.

Factorizar: x^2 − 5x + 6 = (x − 2)(x − 3) = 0.
Soluciones: x = 2 o x = 3 (cada factor = 0).
También puede usarse la fórmula cuadrática: x = [−b ± sqrt(b^2 − 4ac)]/(2a) para ax^2 + bx + c = 0.

Sistemas de ecuaciones

Cuando hay dos o más ecuaciones con varias incógnitas, se habla de sistemas. Métodos comunes:

Sustitución: despejar una variable en una ecuación y sustituirla en la otra.
Eliminación (o suma-resta): combinar ecuaciones para eliminar una variable.
Gráfica: representar ambas ecuaciones y buscar el punto de intersección (útil para visualizar).

Representación gráfica

Las ecuaciones y funciones se pueden representar en el plano cartesiano. Por ejemplo, una función lineal f(x) = mx + b es una recta con pendiente m y ordenada al origen b. La gráfica ayuda a entender comportamiento, intersecciones, máxima y mínima (en casos más avanzados).

Aplicaciones prácticas

Ciencias: modelado de fenómenos físicos (velocidad, crecimiento, decaimiento).
Economía y negocios: cálculo de beneficios, costes, punto de equilibrio, predicción de ingresos.
Ingeniería y construcción: dimensiones, proporciones, cargas y tolerancias.
Tecnología y programación: algoritmos que usan expresiones algebraicas y transformaciones simbólicas.
Estadística y ciencia de datos: regresión lineal y modelos que vinculan variables.

Consejos para aprender álgebra

Practica la manipulación de expresiones: simplificar, factorizar y expandir.
Sigue pasos ordenados al resolver ecuaciones y verifica sustituyendo la solución.
Entiende las propiedades (conmutativa, asociativa, distributiva) y cuándo aplicarlas.
No temas usar gráficos: visualizan relaciones y soluciones de forma clara.
Resuelve muchos ejercicios variados: la fluidez viene con la práctica.

Errores comunes

No aplicar la misma operación a ambos lados de una ecuación.
Olvidar cambiar el sentido de una desigualdad al multiplicar o dividir por un número negativo.
No comprobar las soluciones, especialmente en ecuaciones que pueden introducir raíces o denominadores.

En resumen, el álgebra elemental es la herramienta que permite pasar de cálculos concretos a razonamientos generales y modelar relaciones entre cantidades. Dominar sus conceptos básicos —variables, ecuaciones, funciones y polinomios— abre la puerta a casi todas las áreas científicas y técnicas.

Problemas sencillos de álgebra

Si una ecuación sólo tiene un número desconocido, a veces es fácil de resolver. El número desconocido se llama "x":

2 x + 4 = 12. {2 x + 4 = 12.} $2x+4=12.\,$

Para resolver una ecuación simple con una cantidad desconocida, suma, resta, multiplica o divide ambos lados de la ecuación por el mismo número para poner la cantidad desconocida, x, en un lado de la ecuación. Una vez que x está por sí misma en un lado, utiliza la aritmética para determinar la cantidad en el otro lado de la ecuación. Por ejemplo, restando 4 de ambos lados en la ecuación anterior:

2 x + 4 - 4 = 12 - 4 {\displaystyle 2x+4-4=12-4,} $2x+4-4=12-4\,$

conseguir:

2 x = 8 {\displaystyle 2x=8,} $2x=8\,$

Dividiendo ambos lados por 2:

2 x 2 = 8 2 {\displaystyle {\frac {2x}{2}}={\frac {8}{2},} ${\frac {2x}{2}}={\frac {8}{2}}\,$

conseguir:

x = 4. {\displaystyle x=4,} $x=4.\,$

Puede ser útil pensar en esta ecuación como un balancín o una balanza, lo que se hace a un lado, se debe hacer al otro y el objetivo principal es conseguir que x sea por sí mismo.

Definiciones

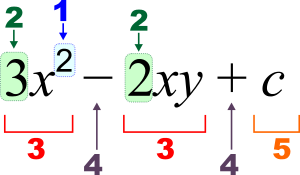
3 x 2 - 2 x y + c {\displaystyle 3x^{2}-2xy+c} $3x^{2}-2xy+c$ tiene las siguientes componentes:

1 : Exponente (potencia), 2 : Coeficiente, 3 : término, 4 : operador, 5 : constante, x , y {\displaystyle x,y} : $x,y$ variables

Preguntas y respuestas

P: ¿Qué es el álgebra elemental?

R: El álgebra elemental es la forma más básica de álgebra que se enseña a los estudiantes. Suele seguir a la aritmética e implica el uso de variables (como a, x, y) para representar números en las ecuaciones.

P: ¿Cuáles son algunos usos del álgebra elemental?

R: El álgebra elemental puede utilizarse para resolver problemas sobre números desconocidos, generalizar reglas de la aritmética, comprender y crear relaciones funcionales, y suele emplearse en muchas otras asignaturas como ciencias, negocios y construcción.

P: ¿Cómo ayuda el álgebra elemental a comprender ideas abstractas?

R: El álgebra elemental ayuda a las personas a aprender ideas generales a partir de muchos ejemplos demostrando que a+b=b+a para todas las a y b. Esto les permite comprender mejor los conceptos abstractos.

P: ¿El álgebra abstracta es más avanzada que el álgebra elemental?

R: Sí, el álgebra abstracta suele enseñarse más tarde en la universidad y es mucho más avanzada que el álgebra elemental.

P: ¿Qué tipos de ecuaciones implica el álgebra elemental?

R: El álgebra elemental implica ecuaciones con variables (como a, x, y) que representan números, así como operadores como +,- ,× ,y ÷ .
3x+1=10 {\displaystyle 3x+1=10}

P: ¿Cómo puede ayudar la comprensión del álgebra elemental con otras asignaturas?

R: Comprender el álgebra elemental puede ayudar con otras asignaturas como las ciencias, los negocios o la construcción, ya que permite resolver problemas sobre números desconocidos y crear relaciones funcionales entre distintas variables.

Buscar dentro de la enciclopedia