Espacio probabilístico
El espacio de probabilidad es un modelo matemático utilizado para describir experimentos científicos Un espacio de probabilidad consta de tres partes:
- Un espacio muestral que recoge todos los resultados posibles
- Un conjunto de eventos. Cada evento asocia cero o más resultados
- Una función que asigna probabilidades a cada evento
Un resultado es el resultado de una única ejecución del modelo. Dado que los resultados individuales pueden tener poca utilidad práctica, se utilizan eventos más complejos para caracterizar grupos de resultados. La colección de todos estos eventos es una σ-álgebra F
. Por último, es necesario especificar la probabilidad de que se produzca cada evento. Esto se hace utilizando la función de medida de la probabilidad, P.
Una vez establecido el espacio de probabilidad, se supone que la "naturaleza" hace su jugada y selecciona un único resultado, ω, del espacio muestral Ω. Se dice que "han ocurrido" todos los sucesos de F que contienen el resultado seleccionado ω (recordemos que cada suceso es un subconjunto de Ω). La selección que realiza la naturaleza se hace de tal manera que si el experimento se repitiera un número infinito de veces, las frecuencias relativas de ocurrencia de cada uno de los sucesos coincidirían con las probabilidades prescritas por la función P.
El destacado matemático soviético Andrey Kolmogorov introdujo la noción de espacio de probabilidad, junto con otros axiomas de probabilidad, en la década de 1930.
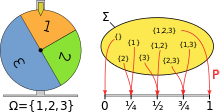
Modelización de una rueda de la fortuna mediante un espacio de probabilidad
Preguntas y respuestas
P: ¿Qué es un espacio de probabilidad?
R: Un espacio de probabilidad es un modelo matemático utilizado para describir experimentos científicos. Consta de tres partes: un espacio muestral que enumera todos los resultados posibles, un conjunto de sucesos que asocian cero o más resultados y una función que asigna probabilidades a cada suceso.
P: ¿En qué consiste el espacio muestral?
R: El espacio muestral consiste en todos los resultados posibles, a menudo escritos como Ω {\displaystyle \Omega } , y un resultado como ω {\displaystyle \omega } .
P: ¿Qué es un resultado?
R: Un resultado es el resultado de una única ejecución del modelo.
P: ¿Para qué se utilizan los sucesos en los espacios de probabilidad?
R: Los sucesos se utilizan para caracterizar grupos de resultados, ya que los resultados individuales pueden tener poca utilidad práctica. La colección de todos esos sucesos se denomina σ-álgebra, a veces escrita como F {\displaystyle {\mathcal {F}} .
P: ¿Cómo se asignan las probabilidades a cada suceso?
R: Las probabilidades se asignan a cada suceso utilizando la función de medida de probabilidad P.
P: ¿Quién introdujo la noción de espacios de probabilidad? R: El destacado matemático soviético Andrey Kolmogorov introdujo la noción de espacios de probabilidad junto con otros axiomas de probabilidad en la década de 1930.
