Postulado de las paralelas de Euclides: definición y geometría euclidiana
Postulado de las paralelas de Euclides: definición clara, ejemplos y su papel en la geometría euclidiana frente a la no euclidiana. Conceptos y aplicaciones esenciales.
En geometría, el postulado de las paralelas es uno de los axiomas de la geometría euclidiana. A veces también se le llama quinto postulado de Euclides, porque es el quinto postulado de los Elementos de Euclides.
El postulado dice que:
Si cortas un segmento de recta con dos líneas, y los dos ángulos interiores que forman las líneas suman menos de 180°, entonces las dos líneas acabarán encontrándose si las extiendes lo suficiente.
El campo de la geometría que sigue todos los axiomas de Euclides se llama geometría euclidiana. Las geometrías que no siguen todos los axiomas de Euclides se llaman geometría no euclidiana.
Formulación moderna y equivalentes
En la notación contemporánea, el postulado suele expresarse de forma más clara y simbólica. Una formulación muy usada —equivalente al postulado original bajo los demás axiomas euclidianos— es el axioma de Playfair:
Por un punto exterior a una recta sólo pasa una recta paralela a la dada.
Existen muchas proposiciones que, junto con los demás axiomas de Euclides, son lógicamente equivalentes al postulado de las paralelas. Entre las más conocidas están:
- La suma de los ángulos interiores de cualquier triángulo es 180°.
- Si una recta corta a dos rectas y las ángulos alternos internos son iguales, las rectas son paralelas.
- Existen rectángulos (un cuadrilátero con cuatro ángulos rectos).
- Las paralelas son únicas por un punto exterior (forma de Playfair).
Historia y esfuerzos por demostrarlo
Desde la Antigüedad y durante muchos siglos los matemáticos intentaron derivar el quinto postulado de los restantes axiomas de Euclides, considerándolo menos evidente que los demás. Numerosos intentos de demostrarlo dieron lugar a resultados parciales y a la introducción de nuevas nociones (como ángulos "infinítos" o límites), pero ninguno logró deducirlo de forma coherente.
En el siglo XIX, gracias al trabajo independiente de matemáticos como János Bolyai, Nikolái Lobachevski y las contribuciones de Carl Friedrich Gauss, se comprendió que el postulado de las paralelas no es deducible de los demás axiomas: su negación conduce a una geometría consistente alternativa (la geometría hiperbólica). La construcción de modelos concretos por Eugenio Beltrami, y más tarde por Klein y Poincaré, demostró la consistencia relativa de la geometría hiperbólica y, por tanto, la independencia del quinto postulado respecto a los demás axiomas de Euclides.
Consecuencias en la geometría euclidiana
Tomando el postulado de las paralelas como verdadero se obtiene una gran parte de la geometría plana clásica: propiedades de triángulos (teorema de la suma de ángulos), semejanza de triángulos, criterios métricos para paralelismo, propiedades de polígonos y del círculo, y herramientas para el cálculo de longitudes y áreas en el plano. Muchas demostraciones y construcciones clásicas dependen de la unicidad de la paralela por un punto exterior.
Geometrías no euclidianas
Si se reemplaza o niega el postulado de las paralelas surgen dos familias principales de geometrías no euclidianas:
- Geometría hiperbólica: por un punto exterior a una recta pasan al menos dos rectas que no se cortan con la dada (infinitas paralelas locales), y la suma de ángulos de un triángulo es menor de 180°.
- Geometría elíptica (o riemanniana): no existen paralelas; todas las rectas se cortan y la suma de ángulos de un triángulo es mayor de 180°.
Estas geometrías no sólo fueron curiosidades teóricas: hoy tienen aplicaciones en relatividad general, en teoría de superficies y en otras áreas de la matemática y la física.
Importancia y perspectiva moderna
El estudio del postulado de las paralelas marcó un cambio profundo en la comprensión de los fundamentos de la matemática: mostró que los axiomas deben elegirse con cuidado y que diferentes sistemas axiomáticos producen geometrías coherentes pero con propiedades distintas. La libertad para modificar o sustituir axiomas básicos es la base de la teoría axiomática moderna.
En resumen, el postulado de las paralelas es central para la geometría euclidiana clásica; su independencia y las geometrías alternativas que surgen al negarlo constituyen uno de los logros más importantes en la historia de la matemática.
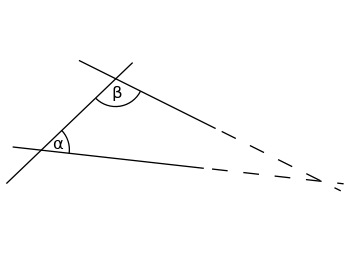
Si la suma de los ángulos interiores α (alfa) y β (beta) es inferior a 180°, las dos rectas se cruzarán en algún punto, si ambas se prolongan hasta el infinito.
Historia
Algunos matemáticos pensaban que el quinto postulado de Euclides era mucho más largo y complicado que los otros cuatro postulados. Muchos de ellos pensaron que se podía demostrar a partir de los otros axiomas más simples. Algunos matemáticos anunciaron que habían demostrado la proposición a partir de las proposiciones más simples, pero todos resultaron estar equivocados.
El axioma de Playfair
Otra proposición más reciente conocida como el axioma de Playfair es similar al quinto postulado de Euclides. Dice que:
Dada una línea recta y un punto que no está en esta línea, sólo se puede trazar una línea recta por este punto que no se encuentre con la otra línea recta.
De hecho, los matemáticos descubrieron que este axioma no sólo es similar al quinto postulado de Euclides, sino que tiene exactamente las mismas implicaciones. Matemáticamente, las dos proposiciones se denominan proposiciones "equivalentes". Hoy en día, el axioma de Playfair es más utilizado por los matemáticos que el postulado paralelo original de Euclides.
Geometría no euclidiana
Con el tiempo, algunos matemáticos intentaron construir nuevas geometrías sin utilizar el axioma. Un tipo de geometría no euclidiana se llama geometría elíptica. En la geometría elíptica el postulado de las paralelas se sustituye por un axioma que establece que:
Dada una línea recta y un punto que no está en esta línea, no se puede dibujar una línea recta que pase por este punto y que no acabe cruzando la otra línea recta.
Los matemáticos descubrieron que, al sustituir el quinto postulado de Euclides por este axioma, podían seguir demostrando muchos de los demás teoremas de Euclides. Una forma de imaginar la geometría elíptica es pensar en la superficie de un globo terráqueo. En un globo terráqueo, las líneas de longitud parecen ser paralelas en el ecuador, pero todas se unen en los polos. A finales del siglo XIX se demostró que la geometría elíptica es consistente. Esto demostró que el quinto postulado de Euclides no era independiente de los demás postulados. Después de esto, los matemáticos dejaron de intentar demostrar el quinto postulado a partir de los otros cuatro postulados. En su lugar, muchos matemáticos comenzaron a estudiar otras geometrías que no siguen el quinto postulado de Euclides.
Otro axioma con el que los matemáticos sustituyen a veces el quinto axioma de Euclides dice que
Dada una línea recta y un punto que no está en esta línea, puedes dibujar al menos dos líneas rectas que pasen por este punto y que finalmente no se crucen con la otra línea recta.
Esto se llama geometría hiperbólica.
Otra geometría simplemente elimina el quinto postulado de Euclides y no lo sustituye por nada. Esto se llama geometría neutra o geometría absoluta.
Buscar dentro de la enciclopedia