Función de Heaviside: definición, propiedades y relación con la delta de Dirac

Descubre la función de Heaviside: definición, propiedades y su vínculo con la delta de Dirac. Aplicaciones y ejemplos claros en teoría de control y procesamiento de señales.

Autor: Leandro Alegsa

21-03-2026 14:14

La función Heaviside, H es una función no continua cuyo valor es cero para una entrada negativa y uno para una entrada positiva.

La función se utiliza en las matemáticas de la teoría de control para representar una señal que se enciende en un momento determinado y permanece encendida indefinidamente. Recibe su nombre del inglés Oliver Heaviside.

La función de Heaviside es la integral de la función delta de Dirac: H′ = δ. A veces se escribe como H(t)=½(1+sgn(t)) o usando la notación habitual de escalón unitario u(t), de modo que

Definición y convenciones

La definición más común de la función escalón unitario es

H(t) = 0 si t < 0, y H(t) = 1 si t > 0.

En t = 0 existen varias convenciones:

H(0) = 0 (alguna literatura de matemáticas).
H(0) = 1 (algunas aplicaciones ingenieriles).
H(0) = 1/2 (convención simétrica, útil en análisis de transformadas y teoría de distribuciones).

Representaciones como límite

La función Heaviside puede obtenerse como límite de funciones continuas que pasan a ser cada vez más escalonadas. Ejemplos:

H(t) = lim_{ε→0+} 1/(1+e^{-t/ε}) (límite de una función logística).
H(t) = lim_{ε→0+} (1/2 + (1/π) arctan(t/ε)) (límite usando arctan).
H(t) = lim_{ε→0+} (1/2)(1 + tanh(t/ε)) (límite usando tanh).
También se puede escribir en términos de la función signo: H(t) = (1 + sgn(t))/2, adoptando la convención sgn(0)=0 para obtener H(0)=1/2.

Relación con la delta de Dirac

En el sentido de distribuciones (derivadas generalizadas) la derivada de la función de Heaviside es la delta de Dirac:

d/dt H(t) = δ(t).

También se tiene la relación inversa por integración:

H(t) = ∫_{-∞}^{t} δ(τ) dτ, interpretada como distribución.

Propiedades útiles

Desplazamiento: H(t - t0) representa un escalón que se activa en t = t0.
Escalado: H(a t) comprime o estira el punto de salto según el factor a (si a>0 mantiene la dirección).
Suma y resta para formar pulsos: H(t - a) - H(t - b) es un pulso que vale 1 en a < t < b y 0 fuera.
Multiplicación por funciones: f(t)H(t - t0) “enciende” la función f a partir de t0, útil para definir funciones por tramos.
Relación con la función signo: H(t) = (1 + sgn(t))/2 bajo la convención apropiada en 0.

Transformadas

Transformada de Laplace (para la convención causal, H(t)=u(t)): L{H(t)} = 1/s, Re(s)>0.
Transformada de Fourier (en el sentido de distribuciones):

F{H(t)} = PV(1/(iω)) + π δ(ω), donde PV indica el valor principal de Cauchy. El resultado refleja que la transformada contiene una parte de valor principal y un componente en frecuencia cero.

Aplicaciones

Modelado de señales que se encienden o apagan (electrónica, teoría de control, procesamiento de señales).
Definición de funciones por tramos y resolución de ecuaciones diferenciales con excitaciones que comienzan en un instante dado.
Uso en convoluciones y respuesta a entradas tipo escalón para sistemas lineales invariantes en el tiempo (análisis de la respuesta al escalón).

Ejemplos rápidos

Pulso unitario entre t=1 y t=3: p(t) = H(t-1) - H(t-3).
Función que coincide con f(t) solo a partir de t0: f(t)H(t-t0).
Respuesta de un sistema al escalón: si y(t) es la respuesta a la delta, la respuesta al escalón es ∫_{0}^{t} y(τ) dτ, lo cual equivale a convolucionar con H(t).

En resumen, la función de Heaviside es una herramienta fundamental en matemáticas aplicadas, física e ingeniería para describir discontinuidades temporales y para relacionar señales y distribuciones mediante integración y derivación en el sentido de distribuciones.

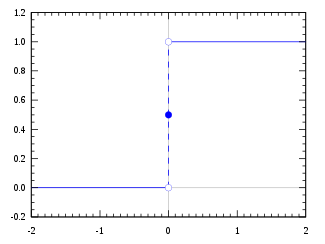
La función escalonada de Heaviside, utilizando la convención del semimáximo

Forma discreta

También podemos definir una forma alternativa de la función escalón de Heaviside como función de una variable discreta n:

H [ n ] = { 0 , n < 0 1 , n ≥ 0 {\displaystyle H[n]={begin{cases}0,&n<0\1,&n\geq 0\cases}} $H[n]={\begin{cases}0,&n<0\\1,&n\geq 0\end{cases}}$

donde n es un número entero.

H ( x ) = lim z → x - ( | z | / z + 1 ) / 2 ) {\displaystyle H(x)=lim _{z\rightarrow x^{-}}((|z|/z+1)/2)} $H(x)=\lim _{z\rightarrow x^{-}}((|z|/z+1)/2)$

El impulso unitario en tiempo discreto es la primera diferencia del paso en tiempo discreto

δ [ n ] = H [ n ] - H [ n - 1 ] . {\displaystyle \delta \left[n\right]=H[n]-H[n-1]. } $\delta \left[n\right]=H[n]-H[n-1].$

Esta función es la suma acumulativa del delta de Kronecker:

H [ n ] = ∑ k = - ∞ n δ [ k ] {\displaystyle H[n]=\sum _{k=-\infty }^{n}\delta [k]\,} $H[n]=\sum _{k=-\infty }^{n}\delta [k]\,$

donde

δ [ k ] = δ k , 0 {\displaystyle \delta [k]=\delta _{k,0},} $\delta [k]=\delta _{k,0}\,$

es la función de impulso unitaria discreta.

Representaciones

A menudo es útil una representación integral de la función escalonada de Heaviside:

H ( x ) = lim ϵ → 0 + - 1 2 π i ∫ - ∞ ∞ 1 τ + i ϵ e - i x τ d τ = lim ϵ → 0 + 1 2 π i ∫ - ∞ ∞ 1 τ - i ϵ e i x τ d τ . {\displaystyle H(x)=lim _{epsilon \}}-a 0^{+}}-{{1}sobre 2\pi \mathrm {i} 1 sobre \tau +mathrm {i} \\N -epsilon }\N -mathrm {e} ^{-\mathrm {i} x\tau }\mathrm {d} \tau ={lim _{epsilon \tau \tau \tau \tau \tau \tau ={lim _{epsilon \tau \tau \tau \tau \tau \tau \tau \tau \tau \tau \tau} 1 sobre \Nmathrm {i} \\N -epsilon }\\Nmathrm {e} ^{mathrm {i} x\tau }\mathrm {d} \N -epsilon. } $H(x)=\lim _{\epsilon \to 0^{+}}-{1 \over 2\pi \mathrm {i} }\int _{-\infty }^{\infty }{1 \over \tau +\mathrm {i} \epsilon }\mathrm {e} ^{-\mathrm {i} x\tau }\mathrm {d} \tau =\lim _{\epsilon \to 0^{+}}{1 \over 2\pi \mathrm {i} }\int _{-\infty }^{\infty }{1 \over \tau -\mathrm {i} \epsilon }\mathrm {e} ^{\mathrm {i} x\tau }\mathrm {d} \tau .$

H(0)

El valor de la función en 0 puede definirse como H(0) = 0, H(0) = ½ o H(0) = 1.

H ( x ) = 1 + sgn ( x ) 2 = { 0 , x < 0 1 2 , x = 0 1 , x > 0. {\displaystyle H(x)={frac {1+\operatorname {sgn}(x)}{2}={comienza{casos}0,&\\frac {1}{2},&x=0\\1,&x>0.\final{casos}} $H(x)={\frac {1+\operatorname {sgn}(x)}{2}}={\begin{cases}0,&x<0\\{\frac {1}{2}},&x=0\\1,&x>0.\end{cases}}$

Páginas relacionadas

Transformación de Laplace

Preguntas y respuestas

P: ¿Qué es la función de Heaviside?

R: La función de Heaviside es una función no continua cuyo valor es cero para una entrada negativa y uno para una entrada positiva.

P: ¿Por qué se utiliza la función de Heaviside en la teoría de control?

R: La función Heaviside se utiliza en la teoría de control para representar una señal que se enciende en un momento determinado y permanece encendida indefinidamente.

P: ¿Quién da nombre a la función de Heaviside?

R: La función Heaviside debe su nombre al inglés Oliver Heaviside.

P: ¿Qué relación existe entre la función de Heaviside y la función delta de Dirac?

R: La función de Heaviside es la integral de la función delta de Dirac: H′(x)= δ(x).

P: ¿Cuál es el resultado de la función de Heaviside para entradas positivas?

R: La función de Heaviside da como resultado uno para entradas positivas.

P: ¿Cuál es el resultado de la función Heaviside para entradas negativas?

R: La función Heaviside da como resultado cero para entradas negativas.

P: ¿Qué tipo de función es la función Heaviside?

R: La función Heaviside es una función no continua.

Buscar dentro de la enciclopedia