Sistema binario: qué es, cómo funciona y su importancia en la informática
Descubre qué es el sistema binario, cómo funciona y por qué es clave en informática: datos, ejemplos y aplicaciones prácticas para entender cómo los ordenadores usan 0 y 1.
El binario es un sistema numérico de base 2. Es de base 2 porque utiliza dos números posibles: 0 y 1. El decimal, el sistema que utiliza la mayor parte del mundo en la vida cotidiana, es un sistema de base 10: utiliza 10 caracteres (0-9). Cuando se escriben los números binarios, se añade un subíndice "(2)" para distinguirlos del mismo número en base 10.
Los ordenadores funcionan en binario, porque los cables pueden almacenar información de dos maneras diferentes: estando alimentados o sin estarlo. Los conjuntos de números binarios pueden utilizarse para representar cualquier información, como texto, audio o vídeo.
Cómo funciona el sistema binario
El sistema binario es un sistema posicional: cada cifra (bit) tiene un valor según su posición, igual que en el sistema decimal. En binario, las potencias de la base 2 determinan el valor de cada posición: 1, 2, 4, 8, 16, etc. Por ejemplo, el número 1101(2) representa:
- 1×8 + 1×4 + 0×2 + 1×1 = 13 en decimal.
En informática, la unidad mínima de información es el bit (binary digit), que puede ser 0 o 1. Un conjunto de 8 bits forma un byte, que es una unidad habitual para medir memoria y almacenamiento.
Conversión entre decimal y binario (método práctico)
Conversión de decimal a binario (método de divisiones):
- Toma el número decimal y divídelo por 2.
- Anota el resto (0 o 1).
- Divide el cociente por 2 y repite hasta que el cociente sea 0.
- Lee los restos en orden inverso; ese es el número binario.
Ejemplo: 13 en decimal →
- 13 ÷ 2 = 6 resto 1
- 6 ÷ 2 = 3 resto 0
- 3 ÷ 2 = 1 resto 1
- 1 ÷ 2 = 0 resto 1
- Lectura inversa: 1101(2) → 13(decimal)
Conversión de binario a decimal (método posicional):
- Multiplica cada bit por 2 elevado a la posición correspondiente (empezando por 0 desde la derecha) y suma los resultados.
Operaciones básicas en binario
Las operaciones aritméticas en binario siguen reglas sencillas:
- 0 + 0 = 0
- 0 + 1 = 1
- 1 + 0 = 1
- 1 + 1 = 10 (se escribe 0 y se lleva 1, igual que en decimal cuando 5+5 = 10)
- 1 + 1 + 1 = 11 (es decir, 3 en decimal)
Estas operaciones se implementan en hardware mediante puertas lógicas (AND, OR, XOR, NOT) que componen sumadores y otros circuitos aritméticos.
Representación de números negativos
Para representar números negativos en binario se usan varios métodos; el más común en la informática moderna es el complemento a dos. Procedimiento para n bits:
- Escribe el valor absoluto en binario con n bits.
- Invierte todos los bits (complemento a uno).
- Suma 1 al resultado.
Ejemplo en 4 bits: +5 = 0101 → invertir → 1010 → sumar 1 → 1011. Así, 1011(2) representa −5 en complemento a dos (en un sistema de 4 bits).
Fracciones y punto binario
El sistema binario también puede representar fracciones usando una "coma" o punto binario. Las posiciones a la derecha del punto valen 1/2, 1/4, 1/8, etc. Por ejemplo:
- 0.1(2) = 1/2 = 0.5 decimal
- 0.01(2) = 1/4 = 0.25 decimal
Bit, byte y múltiplos
- Bit: unidad mínima (0 o 1).
- Byte: 8 bits.
- Múltiplos habituales: kilobyte (KB, 1 000 ó 1 024 bytes según contexto), megabyte (MB), gigabyte (GB), etc.
Aplicaciones e importancia en la informática
El valor práctico del sistema binario en informática es enorme. Algunas aplicaciones clave:
- Almacenamiento y memoria: todo en discos, SSDs y memorias RAM se almacena como bits agrupados en bytes.
- Procesamiento: la CPU realiza operaciones binarias a nivel de circuitos lógicos.
- Codificación de texto: estándares como ASCII o UTF-8 asignan códigos binarios a caracteres (por ejemplo, 'A' = 65 decimal = 01000001(2) en ASCII).
- Multimedia: imágenes, audio y vídeo se codifican como secuencias de bits según formatos (JPEG, MP3, MP4, etc.).
- Redes: las direcciones IP y protocolos usan representaciones binarias; por ejemplo, una dirección IPv4 se suele dividir en cuatro octetos (bytes).
- Detección de errores: técnicas como bits de paridad, checksums y códigos correccionales añaden información binaria para detectar y corregir errores.
Por qué es fundamental el binario
El uso del binario se debe a su simplicidad y robustez para el hardware: representar dos estados (por ejemplo, encendido/apagado, alto/bajo voltaje) es más sencillo y fiable que distinguir múltiples niveles. Esa simplicidad ha permitido construir dispositivos rápidos, compactos y económicos que procesan y almacenan grandes cantidades de información mediante operaciones binarias.
Resumen práctico
- El binario usa sólo 0 y 1 y es un sistema posicional basado en potencias de 2.
- Es la base de toda la informática moderna: procesamiento, memoria, comunicación y almacenamiento.
- Comprender conversiones, operaciones y representación de negativos (complemento a dos) es útil para trabajar con máquinas y entender cómo se maneja la información a bajo nivel.
Sistema numérico
Cuando se introducen los números binarios, ayuda volver a pensar en cómo funcionan los números de base 10 o decimales. Consideremos el número 1101(10) (base 10). Identificamos este número como mil, cien, uno porque tiene un 1 en el lugar de los miles, un 1 en el lugar de las centenas y un 1 en el lugar de las unidades. Pero como los lugares representan 8, 4, 2 y 1 en binario, en lugar de 1000, 100, 10 y 1, el valor convertido a decimal (base 10) sería 8 + 4 + 1 = 13 (10).
Por ejemplo, el número binario 101(2) es 5 en decimal. El bit de la derecha es 1 y tiene un valor de 1 (2^0). El bit del medio tiene un valor de 2 (2^1 o simplemente 2), pero es un 0, por lo que no se suma. El bit de la izquierda es 1 y tiene un valor de 4 (2^2 o 2 * 2). Los bits que son 1s tienen valores de 1 y 4. 1 + 4 = 5.
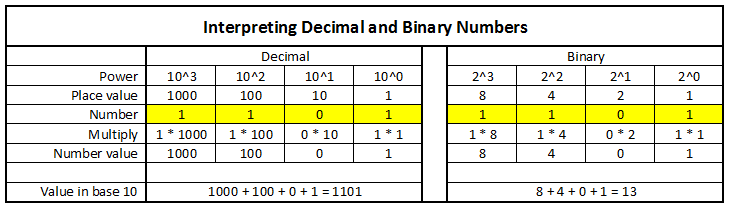
Cómo se interpretan los números decimales y binarios
Ordenadores
Todos los ordenadores utilizan el binario en el nivel más bajo. La mayoría de las memorias duras, como los discos compactos y los DVD, utilizan el binario para representar archivos grandes.
En informática, ocho bits binarios juntos se denominan bytes. El tamaño de los archivos se suele medir en kilobytes o megabytes (a veces en gigabytes). Un kilobyte son 1000 bytes. Un megabyte son 1000 kilobytes, un gigabyte son 1000 megabytes y un terabyte son 1000 gigabytes. A veces, es más fácil medir los bytes en grupos de 1024, ya que 1024 es una potencia de 2. Hay 1024 bytes en un kibibyte, 1024 kibibibytes en un mebibyte y 1024 mebibytes en un gibibyte.
Preguntas y respuestas
P: ¿Qué es binario?
R: Binario es un sistema numérico de base 2 que utiliza dos números posibles: 0 y 1.
P: ¿Por qué el binario es un sistema de base 2?
R: El binario es un sistema de base 2 porque utiliza dos números posibles: 0 y 1.
P: ¿Cuál es la diferencia entre binario y decimal?
R: El binario es un sistema de base 2 y utiliza dos números posibles, mientras que el decimal es un sistema de base 10 y utiliza diez caracteres (0-9).
P: ¿Por qué los ordenadores funcionan en binario?
R: Los ordenadores funcionan en binario porque los cables pueden almacenar información de dos formas distintas: estando alimentados o no.
P: ¿Cómo se utilizan los números binarios?
R: Se pueden utilizar conjuntos de números binarios para representar cualquier información, como texto, audio o vídeo.
P: ¿En qué se diferencian los números binarios de los decimales?
R: Los números binarios se distinguen de los decimales añadiendo un subíndice "(2)" cuando se escriben.
P: ¿Qué caracteres se utilizan en el sistema numérico decimal?
R: El sistema numérico decimal utiliza diez caracteres: 0-9.
Buscar dentro de la enciclopedia