Efecto avalancha en criptografía: qué es y por qué importa
Efecto avalancha en criptografía: cómo un mínimo cambio en la entrada provoca grandes cambios en salida, clave para la seguridad de cifrados y funciones hash frente a ataques.
El efecto avalancha ("landslide effect") es una propiedad crucial de los algoritmos de cifrado por bloques y de las funciones hash criptográficas. Se busca habitualmente en la criptografía porque garantiza que una pequeña modificación en la entrada provoque un cambio grande e impredecible en la salida. En los buenos cifradores de bloque esto significa que un pequeño cambio en la clave o en el texto plano debe causar un cambio drástico en el texto cifrado.
Cómo funciona y por qué importa
El efecto avalancha describe la rápida propagación de cambios cuando el algoritmo aplica suficientes iteraciones o rondas. Así, idealmente cada bit de la salida debe depender de manera compleja de cada bit de la entrada. Esto proporciona dos propiedades deseables en criptografía:
- Confusión: oculta la relación entre clave y salida (relacionado con la propiedad de confusión de Shannon).
- Difusión: cualquier cambio pequeño en la entrada se distribuye por gran parte de la salida.
Si un cifrado por bloques o una función hash no satisface suficientemente el efecto avalancha, su aleatorización es pobre y un criptoanalista podrá hacer predicciones sobre la entrada conociendo solo la salida, lo que facilita ataques como la diferencial o la lineal criptanálisis y puede llevar a romper parcial o totalmente el algoritmo.
Cómo se mide (criterios y pruebas)
Una medida práctica y habitual es la tasa de cambio media: al cambiar un solo bit de entrada (o de la clave) se espera que aproximadamente el 50% de los bits de salida cambien. Dos conceptos importantes relacionados son:
- Criterio de avalancha: cambios de entrada pequeños deben producir cambios grandes en salida.
- Criterio estricto de avalancha (SAC): propuesto para cuantificar que, al invertir un bit de entrada, cada bit de salida cambie con probabilidad 1/2.
Pruebas típicas:
- Invertir sistemáticamente cada bit de entrada (o de la clave) y medir la fracción de bits de salida que cambian.
- Realizar pruebas estadísticas sobre muchas entradas (p. ej. miles) para estimar la media y la varianza de los cambios.
- Usar baterías de tests criptográficos y de aleatoriedad para detectar sesgos o correlaciones.
Ejemplos y consecuencias prácticas
Muchos diseños modernos (por ejemplo, AES y funciones de la familia SHA) implementan rondas, sustituciones y permutaciones pensadas para maximizar confusión y difusión, logrando así un fuerte efecto avalancha. Cuando el efecto avalancha es insuficiente, se abren vectores de ataque:
- La criptoanálisis diferencial explota correlaciones entre entradas que cambian y las diferencias observadas en salidas.
- La criptoanálisis lineal aprovecha relaciones lineales parciales si la difusión es baja.
- Para funciones hash, una mala aleatorización puede facilitar la búsqueda de colisiones o preimágenes.
Cómo se consigue en el diseño
Diseñadores criptográficos buscan deliberadamente el efecto avalancha mediante:
- Capas iterativas de transformación (sustitución y permutación), de ahí que muchos cifradores de producto utilicen rondas repetidas.
- Funciones no lineales (S-boxes) que mezclan bits de forma compleja.
- Mesclas y expansiones de clave (schedules) que eviten correlaciones entre rondas.
- Bloques de datos adecuados y estructuras internas en las funciones hash para propagar cambios ampliamente.
Matemáticamente esto guarda relación con el efecto mariposa: pequeñas variaciones iniciales conducen a diferencias grandes e impredecibles en el resultado final.
Pruebas prácticas simples
Un procedimiento sencillo para comprobar el efecto avalancha en un algoritmo es:
- Seleccionar una entrada X y calcular la salida Y = f(X).
- Invertir un bit de X → X' y calcular Y' = f(X').
- Contar el número de bits distintos entre Y y Y' y calcular la proporción respecto al tamaño de salida.
- Repetir para muchos X y para cada bit de entrada; para un buen diseño esa proporción tenderá a ~50% en promedio.
Resumen
El efecto avalancha es una propiedad esencial para la seguridad práctica de cifradores y funciones hash: proporciona ocultamiento de la relación entrada-salida y resistencia frente a técnicas de criptoanálisis. Por eso es uno de los objetivos principales en el diseño de cualquier cifrado fuerte o función hash criptográfica.
El término efecto avalancha fue utilizado por primera vez por Horst Feistel (Feistel 1973). Posteriormente, el concepto se conectó con la propiedad de confusión de Shannon, que junto con la difusión conforman las bases del diseño criptográfico moderno.
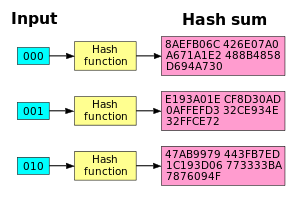
La función hash SHA1 tiene un buen efecto de avalancha. Cuando se cambia un solo bit, la suma del hash se vuelve completamente diferente.
Nombre
El origen del nombre son los desprendimientos de tierra. Una pequeña roca puede caer, ir junto con algo de nieve y hacer un desprendimiento destructivo. La roca era pequeña, pero podía causar muchos destrozos. Es lo mismo que hace este efecto. Un pequeño cambio en la entrada (la roca) debe cambiar la salida (el paisaje).
Criterio estricto de avalancha
El criterio de avalancha estricto (SAC; un "criterio de avalancha fuerte") es una propiedad de las funciones booleanas. Es importante para la criptografía. Se cumple si todos los bits de salida cambian con una probabilidad del 50%, si se cambia un solo bit de entrada.
El SAC se basó en los conceptos de integridad de la evolución y avalancha. Fue introducido por Webster y Tavares en 1985. Hoy en día es un requisito para cualquier sistema criptográfico moderno. Por ejemplo, lo han cumplido todos los finalistas del concurso AES.
Criterio de independencia de los bits
El criterio de independencia del bit (BIC; un criterio independiente del bit) es un criterio. Dice así: Cuando se cambia un solo bit de entrada (invertido), dos bits de salida deben cambiar independientemente el uno del otro. Esto se aplica a todos los bits.
Por ejemplo, no se satisfaría si un bit de salida sólo cambia cuando el otro bit de salida también cambia. Puede que sólo cambien porque el bit de entrada ha cambiado. De lo contrario, los bits de salida dependerían unos de otros.
Páginas relacionadas
- Confusión y difusión
Preguntas y respuestas
P: ¿Qué es el efecto avalancha?
R: El efecto avalancha (también conocido como "efecto desprendimiento") es una propiedad de los cifradores de bloques y de los algoritmos de funciones hash criptográficas que establece que un pequeño cambio en la clave o en el texto plano debería provocar un fuerte cambio en el texto cifrado.
P: ¿Quién utilizó por primera vez el término "efecto avalancha"?
R: El término efecto avalancha fue utilizado por primera vez por Horst Feistel en 1973.
P: ¿Qué relación tiene con la propiedad de confusión de Shannon?
R: El concepto de efecto avalancha fue identificado por la propiedad de confusión de Shannon, que establece que si un cifrado por bloques o una función hash criptográfica no satisface este grado en un grado significativo, entonces tiene una aleatoriedad deficiente y puede ser parcial o completamente rota (craqueada).
P: ¿Cuáles son algunos de los objetivos de diseño a la hora de crear cifrados fuertes?
R: Cuando la gente crea cifradores fuertes intenta construir en ellos un buen efecto de avalancha utilizando principios matemáticos como el efecto mariposa. Esta es la razón por la que la mayoría de los cifradores de bloque son cifradores de producto y por la que las funciones hash tienen grandes bloques de datos.
P: ¿Qué ocurre si un algoritmo no satisface el efecto avalancha?
R: Si un algoritmo no satisface el efecto avalancha en un grado significativo, entonces tiene una aleatorización pobre y puede ser parcial o completamente roto (crackeado) por criptoanalistas que puedan hacer predicciones sobre la entrada basándose sólo en la salida dada.
P: ¿Por qué la mayoría de los cifradores de bloque utilizan cifradores de producto?
R: La mayoría de los cifradores de bloque utilizan cifradores de producto porque ayudan a construir en ellos buenos efectos de aval mediante principios matemáticos como el efecto mariposa.
P: ¿Por qué las funciones hash tienen grandes bloques de datos?
R: Las funciones hash tienen grandes bloques de datos porque ayudan a crear buenos efectos de aval utilizando principios matemáticos como el efecto mariposa.
Buscar dentro de la enciclopedia