Regresión lineal | una forma de ver cómo cambia algo cuando cambian otras cosas utilizando las matemáticas
La regresión lineal es una forma de observar cómo cambia algo cuando cambian otras cosas utilizando las matemáticas. Una regresión lineal utiliza una variable dependiente y una o más variables explicativas para crear una línea recta. Esta línea recta se conoce como "línea de regresión".
La regresión lineal fue la primera de las muchas formas de realizar el análisis de regresión. Esto se debe a que los modelos que dependen linealmente de sus parámetros desconocidos son más fáciles de ajustar que los modelos que están relacionados de forma no lineal con sus parámetros. Otra ventaja de la regresión lineal es que las propiedades estadísticas de los estimadores resultantes son más fáciles de determinar.
La regresión lineal tiene muchos usos prácticos. La mayoría de las aplicaciones se encuadran en una de las dos grandes categorías siguientes:
- La regresión lineal puede utilizarse para ajustar un modelo predictivo a un conjunto de valores observados (datos). Esto es útil, si el objetivo es la predicción, el pronóstico o la reducción. Después de desarrollar un modelo de este tipo, si a continuación se da un valor adicional de X sin que le acompañe el valor de y, el modelo ajustado puede utilizarse para hacer una predicción del valor de y (que se escribe como
). - Dada una variable y y una serie de variables X1 , ..., Xp que pueden estar relacionadas con y, se puede aplicar el análisis de regresión lineal para cuantificar la fuerza de la relación entre y y las Xj , para evaluar qué Xj no tiene ninguna relación con y y para identificar qué subconjuntos de las Xj contienen información redundante sobre y.
Los modelos de regresión lineal intentan que la distancia vertical entre la línea y los puntos de datos (es decir, los residuos) sea lo más pequeña posible. Esto se llama "ajustar la línea a los datos". A menudo, los modelos de regresión lineal tratan de minimizar la suma de los cuadrados de los residuos (mínimos cuadrados), pero existen otras formas de ajuste. Incluyen la minimización de la "falta de ajuste" en alguna otra norma (como con la regresión de desviaciones mínimas absolutas), o la minimización de una versión penalizada de la función de pérdida de mínimos cuadrados, como en la regresión de cresta. El enfoque de mínimos cuadrados también puede utilizarse para ajustar modelos que no son lineales. Como se ha señalado anteriormente, los términos "mínimos cuadrados" y "modelo lineal" están estrechamente relacionados, pero no son sinónimos.
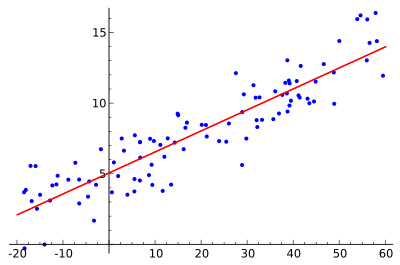
La idea es encontrar la curva roja, los puntos azules son muestras reales. Con la regresión lineal, todos los puntos pueden conectarse mediante una única línea recta. En este ejemplo se utiliza la regresión lineal simple, en la que se minimiza el cuadrado de la distancia entre la línea roja y cada punto de la muestra.
Uso
Economía
La regresión lineal es la principal herramienta analítica en economía. Por ejemplo, se utiliza para adivinar el gasto en consumo, el gasto en inversión fija, la inversión en inventarios, las compras de las exportaciones de un país, el gasto en importaciones, la demanda de posesión de activos líquidos, la demanda de trabajo y la oferta de trabajo.
Preguntas y respuestas
P: ¿Qué es la regresión lineal?
R: La regresión lineal es una forma de observar cómo cambia algo cuando cambian otras cosas utilizando las matemáticas. Utiliza una variable dependiente y una o más variables explicativas para crear una línea recta, conocida como "línea de regresión".
P: ¿Cuáles son las ventajas de la regresión lineal?
R: Los modelos que dependen linealmente de sus parámetros desconocidos son más fáciles de ajustar que los modelos que están relacionados de forma no lineal con sus parámetros. Además, las propiedades estadísticas de los estimadores resultantes son más fáciles de determinar.
P: ¿Cuáles son algunos de los usos prácticos de la regresión lineal?
R: La regresión lineal puede utilizarse para ajustar un modelo predictivo a los valores observados (datos) con el fin de realizar predicciones, pronósticos o reducciones. También puede utilizarse para cuantificar la fuerza de las relaciones entre las variables e identificar subconjuntos de datos que contienen información redundante sobre otra variable.
P: ¿Cómo intentan los modelos de regresión lineal minimizar los errores?
R: Los modelos de regresión lineal intentan que la distancia vertical entre la línea y los puntos de datos (los residuos) sea lo más pequeña posible. Esto se hace minimizando la suma de cuadrados de los residuos (mínimos cuadrados), la falta de ajuste en alguna otra norma (desviaciones mínimas absolutas) o minimizando una versión penalizada de la función de pérdida de mínimos cuadrados (regresión de cresta).
P: ¿Es posible que los modelos de regresión lineal no se basen en los mínimos cuadrados?
R: Sí, es posible que los modelos de regresiones lineales no se basen en los mínimos cuadrados, sino que utilicen métodos como la minimización de la falta de ajuste en alguna otra norma (desviaciones mínimas absolutas) o la minimización de una versión penalizada de la función de pérdida de mínimos cuadrados (regresión de cresta).
P: ¿Son sinónimos "modelo lineal" y "mínimos cuadrados"?
R: No, no son sinónimos. Aunque están estrechamente relacionados, "modelo lineal" se refiere específicamente a la utilización de una línea recta, mientras que "mínimos cuadrados" se refiere específicamente a intentar minimizar los errores asegurándose de que haya una distancia vertical mínima entre la línea y los puntos de datos.
