Ajuste de curvas
El ajuste de curvas consiste en construir una función matemática que se ajuste lo mejor posible a un conjunto de puntos de datos.
El ajuste de la curva puede implicar la interpolación o el suavizado. La interpolación requiere un ajuste exacto de los datos. Con el suavizado, se construye una función "suave" que se ajusta a los datos de forma aproximada. Un tema relacionado es el análisis de regresión, que se centra más en cuestiones de inferencia estadística, como el grado de incertidumbre presente en una curva que se ajusta a datos observados con errores aleatorios.
Las curvas ajustadas pueden utilizarse para ayudar a la visualización de los datos, para adivinar los valores de una función cuando no hay datos disponibles y para resumir las relaciones entre dos o más variables. La extrapolación se refiere al uso de una curva ajustada más allá del rango de los datos observados. Está sujeta a un grado de incertidumbre, ya que puede reflejar el método utilizado para construir la curva tanto como los datos observados.
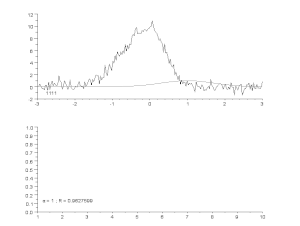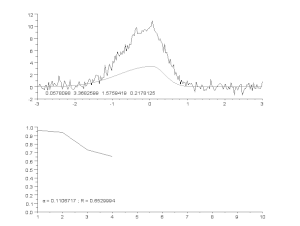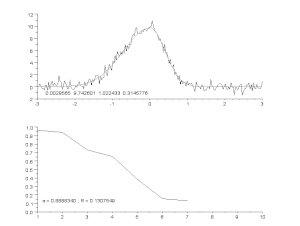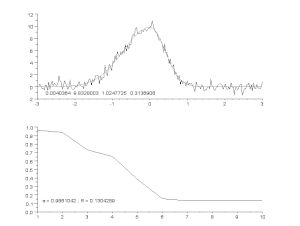
Ajuste de una curva ruidosa mediante un modelo de pico asimétrico, con un proceso iterativo (algoritmo de Gauss-Newton con factor de amortiguación variable α). Arriba: datos brutos y modelo. Abajo: evolución de la suma normalizada de los cuadrados de los errores.
Preguntas y respuestas
P: ¿Qué es el ajuste de curvas?
R: El ajuste de curvas es el proceso de crear una función matemática que se ajuste lo mejor posible a un conjunto de puntos de datos.
P: ¿Cuáles son los dos tipos de ajuste de curvas?
R: Los dos tipos de ajuste de curvas son la interpolación y el suavizado.
P: ¿Qué es la interpolación?
R: La interpolación es un tipo de ajuste de curvas que requiere un ajuste exacto a los datos.
P: ¿Qué es el suavizado?
R: El suavizado es un tipo de ajuste de curvas que construye una función "suave" que se ajusta aproximadamente a los datos.
P: ¿Qué es el análisis de regresión?
R: El análisis de regresión es un tema relacionado que se centra en cuestiones de inferencia estadística, como cuánta incertidumbre hay en una curva que se ajusta a datos observados con errores aleatorios.
P: ¿Cuáles son algunos usos de las curvas ajustadas?
R: Las curvas ajustadas pueden utilizarse para ayudar a visualizar datos, adivinar valores de una función cuando no se dispone de datos y resumir relaciones entre dos o más variables.
P: ¿Qué es la extrapolación?
R: La extrapolación es el uso de una curva ajustada más allá del rango de los datos observados. Sin embargo, está sujeta a cierto grado de incertidumbre, ya que puede reflejar el método utilizado para construir la curva tanto como los datos observados.
Buscar dentro de la enciclopedia