Fractales: definición, ejemplos y aplicaciones
Fractales: qué son, ejemplos visuales y aplicaciones prácticas en ciencia, tecnología y arte. Explicación clara y ejemplos para entender su belleza y utilidad.
Un fractal es cualquier patrón que, cuando se ve como una imagen, produce una imagen que, cuando se amplía, sigue siendo la misma. Se puede cortar en partes que parecen una versión más pequeña de la imagen con la que se empezó. La palabra fractal fue creada por Benoît Mandelbrot en 1975 a partir de la palabra latina fractus, que significa "roto" o "fracturado". Un ejemplo sencillo es un árbol que se ramifica en ramas más pequeñas, y éstas en ramas más pequeñas y así sucesivamente. Los fractales no sólo son bellos, sino que tienen muchas aplicaciones prácticas.
Propiedades fundamentales
Los fractales se distinguen por varias características clave:
- Auto-similitud: muchas partes del fractal se parecen a la figura completa, ya sea de forma exacta (auto-similitud estricta) o aproximada (auto-similitud estadística).
- Complejidad a distintas escalas: al aumentar la resolución aparecen nuevos detalles; algunos fractales muestran estructura infinita cuando se amplían.
- Dimensión fractal: la medida del tamaño de un fractal no se ajusta necesariamente a un entero (por ejemplo, entre 1 y 2). Esta dimensión cuantifica cuán «compleja» es la estructura a distintas escalas.
- Generación iterativa: muchos fractales se obtienen aplicando repetidamente una regla simple (una función o un conjunto de reglas) sobre una figura inicial.
Ejemplos matemáticos y naturales
Existen fractales puramente matemáticos y estructuras fractales en la naturaleza:
- Fractales matemáticos famosos: el conjunto de Mandelbrot, los conjuntos de Julia, el triángulo de Sierpiński, la curva de Koch y el conjunto de Cantor.
- Ejemplos en la naturaleza: costas y líneas de playa, sistemas de ríos, nubes, montañas, bróquiles romanesco, y órganos biológicos como los pulmones o las redes vasculares. El ejemplo intuitivo de un árbol que se ramifica ilustra cómo una misma pauta se repite en distintas escalas.
Métodos de generación
Algunas técnicas habituales para crear fractales:
- Sistemas de función iterada (IFS): combinan transformaciones afines para construir fractales auto-similares (ej.: triángulo de Sierpiński).
- Algoritmos de escape (escape-time): usados para el conjunto de Mandelbrot y los conjuntos de Julia; se calcula si una iteración diverge y se colorea según la velocidad de escape.
- Sistemas L (L-systems): originados en biología para modelar el crecimiento de plantas, útiles para generar estructuras tipo árbol.
- Fractales aleatorios o estadísticos: como el movimiento browniano fraccionario o los métodos de ruido fractal, empleados para modelar terrenos, nubes y texturas.
Dimensión fractal (explicación sencilla)
La dimensión fractal indica cómo cambia la cantidad de detalle al cambiar la escala. Una forma práctica para estimarla es el método de conteo de cajas (box-counting): se cubre la figura con una cuadrícula de cajas de lado ε y se cuenta cuántas cajas N(ε) contienen parte del fractal. Si N(ε) crece como ε-D, entonces D es la dimensión fractal. Para muchas formas fractales, D no es un número entero, lo que refleja su complejidad intermedia entre dimensiones clásicas.
Aplicaciones prácticas
Los fractales han demostrado utilidad en numerosos campos:
- Gráficos y animación por ordenador: generación realista de paisajes, nubes, texturas y elementos vegetales mediante ruido fractal y L-systems.
- Ingeniería y telecomunicaciones: diseño de antenas fractales compactas con buenas propiedades multibanda y ahorro de espacio.
- Medicina y biología: modelado de vasos sanguíneos, estructuras pulmonares, difusión y crecimiento tumoral; análisis de señales biomédicas mediante medidas fractales.
- Geociencias y recursos: descripción de estructuras porosas, fracturación de rocas y patrones costeros; simulaciones en hidrogeología y exploración de yacimientos.
- Compresión de datos: métodos de compresión fractal aprovechan la auto-similitud para reducir información en imágenes.
- Economía y finanzas: estudio de series temporales y mercados financieros; Mandelbrot aplicó conceptos fractales al comportamiento de precios.
- Arte y diseño: creación de imágenes, música y estructuras arquitectónicas basadas en patrones fractales por su estética y funcionalidad.
Cómo experimentar con fractales
Para quien quiera explorar fractales hay métodos sencillos:
- Construir iterativamente el triángulo de Sierpiński o la curva de Koch a mano o con un programa básico.
- Usar software o bibliotecas (programas de visualización fractal, lenguajes como Python con librerías gráficas) para generar conjuntos de Mandelbrot y Julia y jugar con paletas de color.
- Probar L-systems para modelar crecimiento de plantas y obtener versiones ramificadas similares al árbol del ejemplo.
Breve nota histórica
Benoît Mandelbrot popularizó el término y el estudio moderno de los fractales a mediados del siglo XX al observar que muchos fenómenos naturales presentan irregularidades que no se describen bien con la geometría clásica. Su trabajo conectó ideas de la matemática pura con aplicaciones prácticas en distintas disciplinas.
En conjunto, los fractales ofrecen una forma poderosa de describir y generar estructuras complejas que aparecen tanto en teoría matemática como en la naturaleza y la tecnología. Su estudio combina intuición visual, técnicas computacionales y herramientas matemáticas como la teoría de la medida y la dinámica iterativa.
Un triángulo de Sierpinski, después de 7 iteraciones.
El conjunto de Mandelbrot es un famoso ejemplo de fractal.
Ejemplos
Hay muchos tipos de fractales, realizados de muy diversas maneras. Un ejemplo es el triángulo de Sierpinski, donde hay un número infinito de triángulos pequeños dentro del grande. Otro ejemplo es el conjunto de Mandelbrot, llamado así por Benoît Mandelbrot. El triángulo de Sierpinksi se construye mediante patrones, pero el conjunto de Mandelbrot se basa en una ecuación.
También hay muchos ejemplos naturales de fractales en la naturaleza, como los árboles, los copos de nieve, algunos vegetales y las costas.
La curva de Koch
La curva de Koch es un ejemplo sencillo de fractal. En primer lugar, empieza con una parte de una línea recta, llamada segmento de línea recta. Corta la línea en 3 trozos del mismo tamaño. Deshazte de la parte central de esos trozos, y pon la parte superior de un triángulo cuyos lados tengan la misma longitud que el trozo a cortar. Ahora tenemos 4 segmentos de línea que se tocan en los extremos. Ahora podemos hacer lo que acabamos de hacer con el primer segmento con cada uno de los 4 trozos. Ahora podemos hacer lo mismo una y otra vez a todos los bits que tenemos. Ahora hacemos esto para siempre y miramos lo que tenemos al final.
La longitud de la curva de Koch es infinita, y el área de la curva de Koch es cero. Esto es bastante extraño. Un segmento de línea (con dimensión 1) podría tener una longitud de 1, pero tiene un área de 0. Un cuadrado de longitud 1 y anchura 1 (con dimensión 2) tendrá área 1 y longitud de infinito.
Dimensión de similitud
Así, la curva de Koch parece ser mayor que algo de dimensión 1, y menor que algo de dimensión 2. La idea de la dimensión de similitud es dar una dimensión que dé una mejor idea de la longitud o el área de los fractales. Así que, para una Curva de Koch, queremos una dimensión entre 1 y 2.
La Curva de Koch se puede cortar en cuatro trozos, cada uno de los cuales es 1 3 {\frac {1}{3}}
del tamaño del original. Llamamos N al número de trozos en que se puede cortar un fractal {\displaystyle N} 
, y llamamos B a la diferencia de tamaño {\displaystyle B} 
. Los ponemos en la ecuación:
log N - log B {\displaystyle {\frac {\log N}{-\log B}} 
Donde log {\displaystyle \log }
es el logaritmo de un número. Este número es la Dimensión de Hausdorff del fractal. En la Curva de Koch, es log 4 - log 1 3 = 1,2619... {\displaystyle {\frac {\log 4}{-\frac {1}{3}}}}=1,2619... } 
como queríamos.
La curva de Koch es una de las formas fractales más simples, por lo que su dimensión es fácil de calcular. Su dimensión de similitud y su dimensión de Hausdorff son iguales. Esto no ocurre con los fractales más complejos.
Copo de nieve Koch
El copo de nieve de Koch (o estrella de Koch) es lo mismo que la curva de Koch, excepto que comienza con un triángulo equilátero en lugar de un segmento de línea.
Cómo hacer la curva de Koch
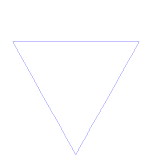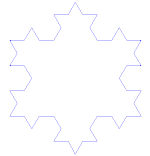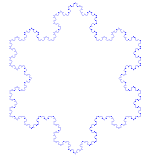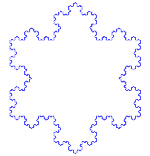
Utiliza
Los fractales tienen muchas aplicaciones, por ejemplo, en biología (pulmón, riñones, variabilidad del ritmo cardíaco, etc.), en terremotos, en finanzas, donde se relacionan con las llamadas distribuciones de cola pesada, y en física. Esto indica que hay que estudiar los fractales para entender por qué son tan frecuentes en la naturaleza.Algunos fractales existen sólo por razones artísticas, pero otros son muy útiles. Los fractales son formas muy eficaces para las antenas de radio y se utilizan en los chips de los ordenadores para conectar eficazmente todos los componentes. También las líneas de costa pueden considerarse fractales.
Preguntas y respuestas
P: ¿Qué es un fractal?
R: Un fractal es cualquier patrón que, cuando se ve como una imagen, produce una imagen que seguirá haciendo la misma imagen cuando se amplía.
P: ¿A quién se atribuye la acuñación del término "fractal"?
R: A Benoît Mandelbrot se le atribuye la acuñación del término "fractal" en 1975.
P: ¿Cuál es la etimología de la palabra "fractal"?
R: La palabra "fractal" procede del latín "fractus", que significa "roto" o "fracturado".
P: ¿Se pueden cortar los fractales en partes?
R: Sí, los fractales pueden cortarse en partes que parecen una versión más pequeña de la imagen con la que empezaron.
P: ¿Puede dar un ejemplo de fractal?
R: Un ejemplo sencillo de fractal es un árbol que se ramifica en ramas más pequeñas, y éstas en ramas más pequeñas, y así sucesivamente.
P: ¿Qué aplicaciones prácticas tienen los fractales?
R: Los fractales tienen muchas aplicaciones prácticas, como los gráficos por ordenador, la medicina, la física y las finanzas.
P: ¿Por qué son importantes los fractales?
R: Los fractales son importantes porque pueden ayudarnos a comprender fenómenos naturales complejos y a crear modelos y simulaciones más precisos.
Buscar dentro de la enciclopedia