Correlación
En estadística y teoría de la probabilidad, la correlación se refiere a la estrecha relación entre dos conjuntos de datos.
La correlación no siempre significa que una cosa cause la otra. Es muy posible que haya un tercer factor implicado.
La correlación suele tener una de dos direcciones. Estas son positivas o negativas. Si es positiva, los dos conjuntos suben juntos. Si es negativa, entonces uno sube mientras el otro baja.
Se utilizan muchas medidas diferentes de correlación para distintas situaciones. Por ejemplo, en un gráfico de dispersión, la gente dibuja una línea de mejor ajuste para mostrar la dirección de la correlación.
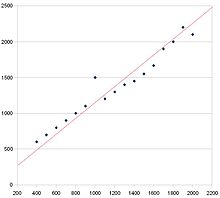
Este gráfico de dispersión tiene una correlación positiva. Se puede decir porque la tendencia es hacia arriba y hacia la derecha. La línea roja es la línea de mejor ajuste.
Explicación de la correlación
Fuerte y débil son palabras utilizadas para describir la correlación. Si la correlación es fuerte, los puntos están muy juntos. Si la correlación es débil, los puntos están separados. Hay formas de hacer que los números muestren lo fuerte que es la correlación. Estas medidas se denominan coeficientes de correlación. El más conocido es el coeficiente de correlación producto-momento de Pearson. Se introducen los datos en una fórmula y se obtiene un número. Si el número es 1 o -1, entonces hay una fuerte correlación. Si la respuesta es 0, entonces no hay correlación. Otro tipo de coeficiente de correlación es el coeficiente de correlación de rango de Spearman.
Correlación frente a causalidad
La correlación no siempre significa que una cosa cause la otra (causalidad), porque otra cosa podría haber causado ambas. Por ejemplo, en los días de calor la gente compra helados, y también va a la playa, donde algunos son devorados por los tiburones. Existe una correlación entre las ventas de helados y los ataques de tiburones (en este caso, ambos aumentan cuando sube la temperatura). Pero el hecho de que las ventas de helados aumenten no significa que las ventas de helados causen (causalidad) más ataques de tiburones o viceversa.
Dado que la correlación no implica causalidad, los científicos, economistas, etc. pondrán a prueba sus teorías creando entornos aislados en los que sólo se modifique un factor (cuando esto sea posible). Sin embargo, los políticos, los vendedores, los medios de comunicación y otros suelen sugerir que una determinada correlación implica causalidad. Esto puede deberse a la ignorancia o al deseo de persuadir. Así, una noticia puede llamar la atención diciendo que las personas que consumen un determinado producto con más frecuencia tienen un determinado problema de salud, dando a entender una causalidad que en realidad podría deberse a otra cosa.
Páginas relacionadas
- Cohen, J., Cohen P., West, S.G., & Aiken, L.S. (2003). Applied multiple regression/correlation analysis for the behavioral sciences. (3ª ed.) Hillsdale, NJ: Lawrence Erlbaum Associates.
Preguntas y respuestas
P: ¿Qué es la correlación?
R: La correlación es una forma de indicar lo estrechamente relacionados que están dos conjuntos de datos.
P: ¿Significa la correlación que un conjunto de datos es la causa del otro?
R: No, la correlación no siempre significa que un conjunto de datos sea la causa del otro. De hecho, a menudo hay un tercer factor implicado.
P: ¿Cuáles son las dos direcciones de la correlación?
R: Las dos direcciones de la correlación son positiva y negativa.
P: ¿Qué significa una correlación positiva?
R: Una correlación positiva significa que los dos conjuntos de datos suben juntos.
P: ¿Qué significa una correlación negativa?
R: Una correlación negativa significa que un conjunto de datos sube mientras que el otro baja.
P: ¿Existen diferentes medidas de correlación?
R: Sí, se utilizan muchas medidas diferentes de correlación para distintas situaciones.
P: ¿Cómo se suele mostrar la dirección de la correlación en un gráfico de dispersión?
R: A menudo se dibuja una línea de mejor ajuste para mostrar la dirección de la correlación en un gráfico de dispersión.
Buscar dentro de la enciclopedia